Authors:
Jian Xu、Shian Du、Junmei Yang、Qianli Ma、Delu Zeng
Paper:
https://arxiv.org/abs/2408.06710
Introduction
Gaussian Process Latent Variable Models (GPLVMs) have gained popularity for unsupervised learning tasks such as dimensionality reduction and missing data recovery. These models are flexible and non-linear, making them suitable for complex data structures. However, traditional methods face challenges in high-dimensional spaces. This paper introduces a novel approach using Stochastic Gradient Annealed Importance Sampling (SG-AIS) to address these issues.
Background
GPLVM Variational Inference
GPLVMs map high-dimensional data to a lower-dimensional latent space using Gaussian Processes (GPs). The Bayesian version of GPLVMs uses sparse representations to reduce model complexity. The evidence lower bound (ELBO) is used as the loss function, and the goal is to make this bound as tight as possible.
Importance-weighted Variational Inference
Importance-weighted variational inference (IWVI) provides a tighter lower bound by sampling multiple times from the proposal distribution. However, this method struggles with high-dimensional latent variables due to the increased variance of the importance weights.
Variational AIS Scheme in GPLVMs
Variational Inference via AIS
Annealed Importance Sampling (AIS) estimates the evidence by transforming the posterior distribution into a sequence of intermediate distributions. This method allows for efficient computation of the evidence, especially when the posterior is difficult to sample from directly.
Time-inhomogeneous Unadjusted Langevin Diffusion
The AIS process uses a Langevin dynamic to sample from the intermediate distributions. This dynamic is easy to sample and optimize, making it suitable for high-dimensional spaces.
Reparameterization Trick and Stochastic Gradient Descent
The reparameterization trick is used to obtain an unbiased estimate of the expectation over the variational distribution. Stochastic gradient descent is then applied to optimize the variational parameters and GP hyperparameters.
Experiments
Methods and Practical Guidelines
The experiments are divided into two sets: one for dimensionality reduction and clustering, and another for image data recovery. The proposed method is compared with classical sparse VI and IWVI methods. The experiments are conducted on a Tesla A100 GPU.
Dimensionality Reduction
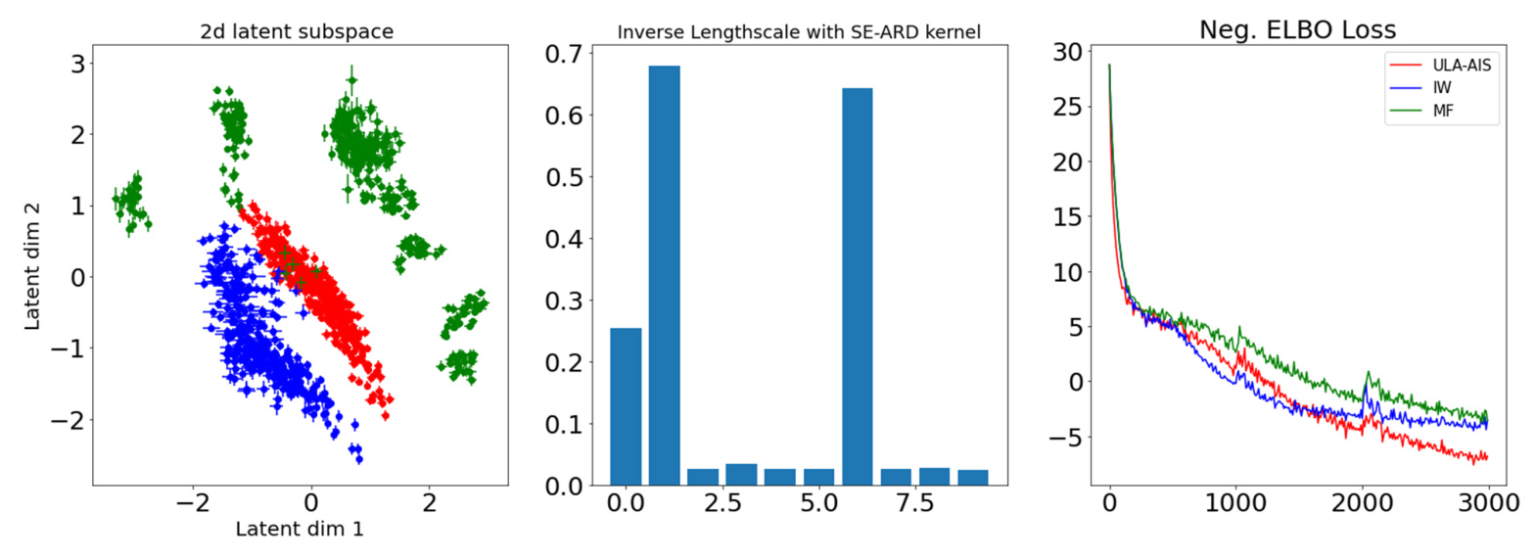
The multi-phase Oilflow data and Wine Quality data are used for dimensionality reduction experiments. The proposed method shows lower reconstruction loss and mean squared error (MSE) compared to IWVI and MF methods.
Make Predictions in Unseen Data
Reconstruction experiments are conducted on the MNIST and Frey Faces datasets. The proposed method demonstrates superior performance in terms of lower variational bounds and higher log-likelihoods.
Conclusion
The proposed SG-AIS method for GPLVMs leverages annealing and Langevin dynamics to achieve tighter variational bounds and better variational approximations in high-dimensional spaces. The experimental results show that the method outperforms state-of-the-art techniques in terms of accuracy and robustness.
Appendix
Euler-Maruyama Discretization
The Euler-Maruyama discretization is used to sample from the Langevin dynamic. This process is reversible, ensuring that the variational distribution gradually moves towards the true posterior distribution.
Stochastic Gradient Descent
Stochastic gradient descent is used to optimize the variational parameters and GP hyperparameters. The method is scalable and can handle large datasets efficiently.
Experimental Configuration
The experimental configuration for the datasets used in the experiments is provided, including the number of data points, data space dimensions, and other relevant parameters.
Comparison of Running Time
The running time of the proposed method is compared with the IW method. The results show that the proposed method is more efficient, especially as the number of iterations increases.
Visualizations
Visualizations of the dimensionality reduction and reconstruction tasks are provided to illustrate the effectiveness of the proposed method.
References
The references cited in the paper provide additional context and background information on the methods and techniques used in the proposed approach.
This blog post provides a detailed interpretation of the paper “Variational Learning of Gaussian Process Latent Variable Models through Stochastic Gradient Annealed Importance Sampling.” The proposed SG-AIS method addresses the limitations of traditional importance sampling techniques and demonstrates superior performance in high-dimensional and complex data spaces.