Authors: Qiyao Liang、Ziming Liu、Mitchell Ostrow、Ila Fiete
ArXiv:https://arxiv.org/abs/2408.13256
Introduction
Diffusion models have demonstrated a remarkable ability to generate realistic images by combining elements in novel ways, a phenomenon known as compositional generalization. Despite their success, the underlying mechanisms that enable these models to achieve compositionality remain poorly understood. Inspired by cognitive neuroscience, this study aims to investigate whether and when diffusion models learn semantically meaningful and factorized representations of combinable features. By training conditional denoised diffusion probabilistic models (DDPMs) on 2D Gaussian data for controlled experiments, we seek to reveal how these models encode and generalize the complexity of component features.
Related Work
The concepts of factorization and compositional generalization have been explored in various deep generative models. Previous studies have produced mixed results on the correlation between factorized representations and compositionality. Some studies have shown that factorization promotes compositionality, while others have found little correlation. The complexity of datasets, which often contain a mixture of discrete and continuous features, has hindered a clear understanding of the representations learned by the models. Recent empirical studies on toy diffusion models have shown that these models can generalize compositionally, but the mechanistic aspects remain unexplored.
Research Methodology
Dataset Generation
We generated grayscale images of size (N \times N) pixels, where N = 32 by default. Each image contains 2D Gaussian bumps or 2D Gaussian stripes and (SOS), centered at different (x, y) coordinates. The brightness of each pixel is determined by a Gaussian function with parameters (\mu _x, \mu _y) (mean) and (\sigma _x, \sigma _y) (standard deviation). The dataset is designed to allow for controllable variations in sparsity and overlap by adjusting the delta (dx, dy) and spread (\sigma _x, \sigma _y).
Model Training and Evaluation
A conditional DDPM with a standard UNet architecture is trained on the generated dataset. Ground truth labels ((\mu _x, \mu _y)) are provided as input to the network. The researchers use dimensionality reduction tools such as PCA and UMAP to visualize and analyze the internal representations learned by the model. Performance is evaluated based on the accuracy of the generated images in correctly displaying the location of the 2D Gaussian centers.
Experimental Design
Experiment 1: Factorized Representations
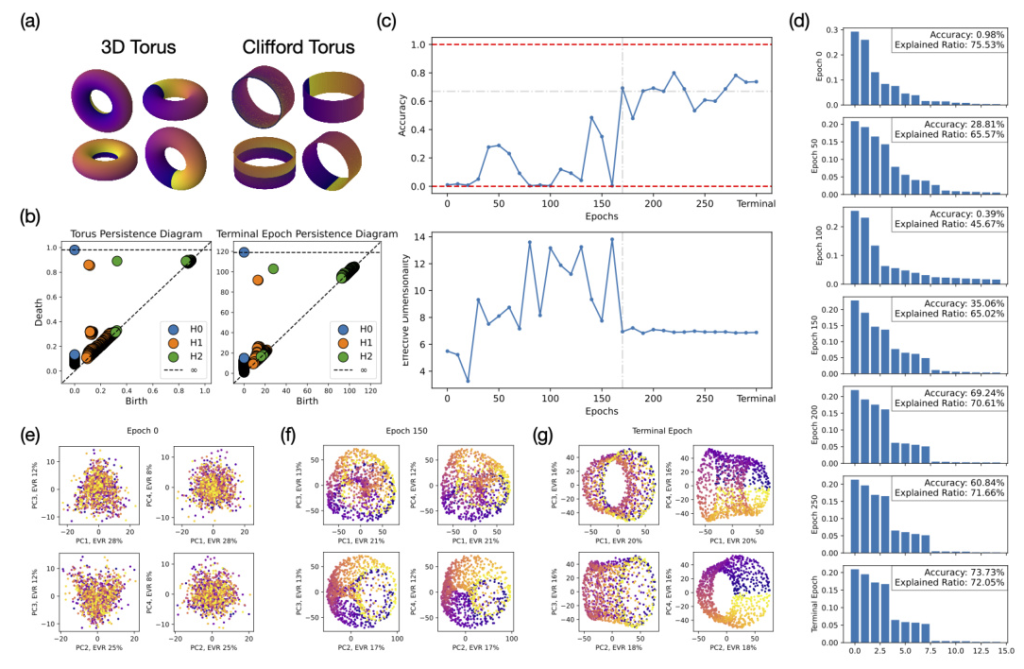
The first experiment aims to determine whether the model has learned factored representations. The researchers impose periodic boundary conditions on the image space, forming a torus that allows them to distinguish between coupled and factored representations. They used persistent homology to compute topological features of the learned representations and confirmed the decomposition using orthogonality and parallelism tests.
Experiment 2: Compositional Generalization
In the second experiment, the researchers tested the model’s combinatorial generalization ability by training on an incomplete dataset. They evaluated the model’s performance in generating 2D Gaussians inside and outside the test region, considering four possible outcomes based on the model’s ability to combine and interpolate.
Experiment 3: Data Efficiency
The third experiment investigated the data efficiency of training the model on a dataset containing isolated variables. The researchers compared the performance of the model trained on 2D Gaussian bumps alone and on 2D Gaussian bumps and 1D Gaussian stripes simultaneously. They analyzed the scaling of data efficiency as a function of image size (N).
Results and Analysis
Factorized Representations
The results show that the model learns a factorized representation, similar to a Clifford torus, where the subspaces encoding (x) and (y) are mostly orthogonal. However, the model treats different values of the same feature in an almost orthogonal manner, indicating a “superfactored” representation. This factorization emerges gradually during training, and the effective dimensionality of the learned representation converges to around 7 dimensions.
Compositional Generalization
The model shows the ability to generalize combinatorially but has difficulty with interpolation. When trained on an incomplete dataset, the model produces high accuracy in one dimension and low accuracy in another dimension over the test region. This suggests that the model can compose independent features but cannot interpolate within a single feature dimension. Adding 1D Gaussian fringes to the training data improves the model’s compositional generalization, highlighting the importance of compositional examples.
Data Efficiency
The study found that models trained on datasets with isolated factors of variation and a small number of compositional examples show significant data efficiency. Compared to quadratic scaling of the baseline dataset, the augmented dataset requires a linear number of data points in (N) to achieve high accuracy. This suggests that training with isolated factors and compositional examples can significantly improve data efficiency
Connection to Percolation Theory
The researchers found a connection between multivariate learning in diffusion models and percolation theory. They hypothesized that the model requires a threshold amount of training data to build a faithful representation of the dataset. Simulation results support this hypothesis, showing that smaller similarities between samples make it harder for the model to learn meaningful representations.
Overall Conclusion
This study provides valuable insights into how diffusion models learn to factorize and combine features. The results show that diffusion models have inductive biases for factorization and compositionality, which are critical for scalability. The results highlight the importance of including isolated factors of variation and combinatorial examples in the training data for achieving efficient and effective generalization. The connection to percolation theory provides a canonical explanation for the emergence of factorized representations, paving the way for more efficient data training methods. Future research should explore these concepts in more complex and realistic datasets to further enhance our understanding of diffusion models.