Authors:
Kenji Harada、Tsuyoshi Okubo、Naoki Kawashima
Paper:
https://arxiv.org/abs/2408.10669
Tensor Tree Learns Hidden Relational Structures in Data to Construct Generative Models
Introduction
In the realm of machine learning, generative models are pivotal for tasks such as data synthesis, anomaly detection, and more. The architecture of these models often needs to be tailored to the specific characteristics of the data. Traditional approaches either manually select the architecture or optimize it through parameter pruning. However, a novel approach leverages the tensor tree network within the Born machine framework to dynamically optimize the network structure, thereby uncovering hidden relational structures in the data. This blog delves into the study by Kenji Harada, Tsuyoshi Okubo, and Naoki Kawashima, which proposes this innovative method and demonstrates its efficacy across various datasets.
Related Work
Tensor Networks and Born Machines
Tensor networks have been employed in various machine learning tasks, including classifiers, neural networks, and reinforcement learning. The Born machine framework, which uses the quantum state measurement process for generative modeling, has shown promise in representing probability distributions through tensor networks. Previous works have utilized one-dimensional chains (tensor trains) and balanced trees for this purpose, but the optimal network structure for a given dataset remains an open question.
Network Structure Optimization
Optimizing the network structure to reflect the data’s relational characteristics is crucial for high-performance generative models. Traditional methods involve manual selection or parameter pruning. Recent advancements propose using tensor networks to represent quantum wave functions, but the challenge lies in dynamically optimizing the network structure to minimize information flow and enhance learning efficiency.
Research Methodology
Adaptive Tensor Tree (ATT) Method
The core idea of the proposed method is to adopt a general tree structure for the tensor network and adaptively reconnect its branches based on the mutual information between data elements. This approach aims to minimize the bond mutual information (BMI), which measures the mutual dependence between two groups of outputs. By dynamically optimizing the tree structure, the method ensures that strongly correlated variables are placed close to each other, reducing unnecessary information flow and improving learning efficiency.
Mutual Information and Tensor Decomposition
The mutual information between two groups of outputs is bounded by the entanglement entropy of the quantum state. By cutting a bond in the tensor tree, the network is decomposed into two sub-trees, and the mutual information between these sub-trees is minimized. The ATT method iteratively combines and decomposes local tensors, guided by the BMI, to optimize the network structure.
Experimental Design
Datasets and Scenarios
The efficacy of the ATT method was demonstrated using four datasets:
1. Random Patterns: Sequences of random binary patterns with long-range correlations.
2. Handwritten Digits (QMNIST): Images of handwritten digits with implicit geometrical relationships among pixels.
3. Bayesian Networks: Data with probabilistic dependencies representing causal relationships.
4. Stock Price Fluctuations (S&P 500): Real-world data with unknown relational structures.
Experimental Setup
For each dataset, the initial tensor network was either a tensor train or a random tensor tree. The ATT method was applied to dynamically optimize the network structure, and the performance was evaluated based on the negative log-likelihood (NLL) of the learned generative models. The results were compared with conventional methods to highlight the improvements achieved by the ATT method.
Results and Analysis
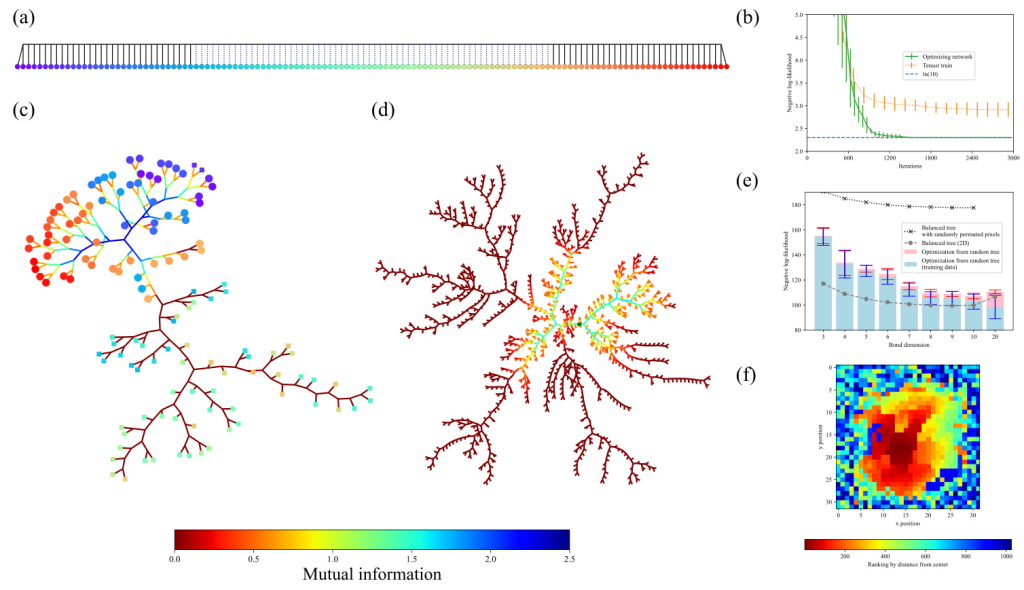
Random Patterns and Handwritten Digits
The ATT method successfully captured the strong correlations in random patterns, clustering relevant variables near the center of the network. For handwritten digits, the optimized network structure aligned with the geometrical relationships among pixels, even without prior knowledge of the data’s spatial arrangement. The NLL values for both datasets demonstrated significant improvements over fixed network structures.
Bayesian Networks
The ATT method effectively identified the causal dependencies in Bayesian networks, reconstructing the correct tree structures from the data. This demonstrates the method’s ability to uncover hidden relational structures and accurately represent them in the tensor network.
Stock Price Fluctuations
For the S&P 500 dataset, the ATT method revealed the sector-wise clustering of companies, reflecting the inherent relational structures in the stock price fluctuations. The optimized network structure showed improved generalization performance, with lower NLL values for both training and testing data.
Overall Conclusion
The study presents a novel approach to generative modeling using the tensor tree network within the Born machine framework. By dynamically optimizing the network structure based on mutual information, the ATT method uncovers hidden relational structures in the data, leading to enhanced performance and insightful representations. The method’s efficacy was demonstrated across various datasets, highlighting its potential as a powerful tool for data analysis and generative modeling.
In summary, the proposed ATT method offers a systematic approach to optimizing generative models, adapting to the information flow hidden in the data, and providing valuable insights into the underlying relational structures. This advancement opens new avenues for research and practical applications in machine learning and data analysis.