Authors:
Xinnan Dai、Qihao Wen、Yifei Shen、Hongzhi Wen、Dongsheng Li、Jiliang Tang、Caihua Shan
Paper:
https://arxiv.org/abs/2408.09529
Introduction
Background
Large Language Models (LLMs) have demonstrated remarkable success in various reasoning tasks, including mathematical problem-solving, commonsense reasoning, and symbolic problem-solving. However, their ability to handle graph reasoning tasks remains under scrutiny. Graph reasoning is crucial for applications such as question-answering systems, autonomous planning, and robot navigation. Despite theoretical studies suggesting that LLMs can handle graph reasoning tasks, empirical evaluations reveal numerous failures.
Problem Statement
This study aims to revisit the graph reasoning ability of LLMs by focusing on three fundamental graph tasks: graph description translation, graph connectivity, and the shortest path problem. The goal is to uncover the limitations of LLMs in understanding graph structures through text descriptions and to propose possible explanations for the observed discrepancies between theoretical capabilities and practical performance.
Related Work
Evaluation on Graph Reasoning Tasks
Recent efforts have been made to evaluate LLMs on graph reasoning tasks. Studies like NLGraph and GraphInstruct have extended the benchmarks for graph reasoning, suggesting that LLMs have preliminary graph reasoning abilities. VisionGraph has even provided a multimodal version of the graph reasoning task benchmark.
Graph Connectivity in Theory
Theoretical studies have shown that LLMs, through their transformer architecture, can simulate every step in a graph algorithm. This suggests that LLMs are capable of handling graph connectivity tasks, such as breadth-first search (BFS) and Dijkstra’s algorithm for the shortest path problem.
LLMs for Graphs in Applications
Despite their theoretical capabilities, LLMs often fail in practical graph reasoning tasks. Recent studies have validated the use of additional tools to enhance LLMs’ comprehension of graphs. For example, GraphEmb employs an encoding function to augment prompts with explicit structured information, and GraphWiz fine-tunes LLMs using graph reasoning datasets.
Theoretical Support for Graph Reasoning Tasks
Theoretical results suggest that LLMs can solve fundamental graph reasoning tasks by deconstructing them into subtasks. For example, graph connectivity and shortest-path tasks can be formulated as decision-making problems solvable by LLMs.
Research Methodology
Graph Description Translation
Graph Descriptions
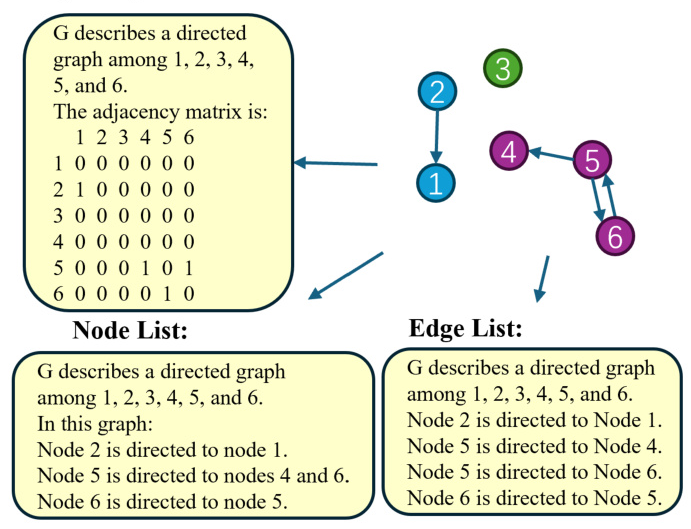
Three types of graph structure description methods are widely used: Adjacency Matrix, Node List, and Edge List. These methods describe the graph’s structure in different ways, as shown in
Translations on Graph Descriptions
To verify LLMs’ ability to understand graph structures, a graph translation description task was designed. This task requires LLMs to use the input graph description to generate various descriptions. The accuracy of these translations was evaluated using GPT-4 and LLAMA3.0-70B.
Graph Connectivity
Connectivity Types
Connectivity types were categorized into K-hops, Singleton, Isolated Components, and Asymmetric, as shown in
Dataset Construction
Graphs were generated with varying numbers of nodes and edges, and samples were collected for different connectivity types. The dataset was divided into Easy, Medium, and Hard levels based on the number of nodes.
Evaluation Metrics
Two novel metrics, FidelityAcc (Facc) and Path Consistency Ratio (PCR), were introduced to evaluate the correctness of reasoning paths and the consistency of paths selected by LLMs.
Shortest Path Problem
The shortest path problem was studied using both unweighted and weighted graphs. The performance of LLMs was evaluated on these datasets to understand their ability to handle more complex graph reasoning tasks.
Experimental Design
Planning and Designing the Experiment
Experiments were conducted using GPT-4, GPT-3, and LLAMA 3 with zero-shot settings. The datasets included both directed and undirected graphs with varying levels of difficulty.
Preparing the Data and Conditions
Graphs were randomly generated with node numbers ranging from 5 to 25. The datasets were divided into Easy, Medium, and Hard levels. Different naming methods for nodes were also evaluated to understand their impact on LLM performance.
Results and Analysis
Graph Description Translation
The results indicated that LLMs struggle with graph description translations, achieving reliable accuracy only when the source and target descriptions are identical. Performance declined significantly when translating between different types of descriptions, as shown in
Graph Connectivity
Undirected Graph Results
GPT-4 demonstrated better reasoning ability compared to GPT-3 and LLAMA 3 across all cases. The difficulty of reasoning increased with the path length, and Node Lists generally performed better than Edge Lists, as shown in
Directed Graph Results
LLMs had lower performance on directed graphs, particularly in the Asymmetric dataset. Descriptions using Node Lists outperformed those using Edge Lists, as shown in
Shortest Path Problem
The performance of LLMs on the shortest path problem aligned with observations from graph connectivity tasks. Performance diminished as the path length increased, and undirected graphs consistently outperformed directed graphs, as shown in
Analysis of Other Factors
Impact of Algorithm Prompts
In-context learning approaches, such as Chain-of-Thought (CoT), were revisited. Few-shot examples helped LLMs recognize isolated components, and the Dijkstra-CoT method improved performance in the shortest path cases, as shown in
Influence of Node Names
Different naming methods for nodes yielded varied results. Sequentially ordered node names enhanced LLM performance, suggesting that LLMs could leverage memory recognition to predict connectivity more effectively, as shown in
Overall Conclusion
This study revisited the graph reasoning ability of LLMs by focusing on three fundamental tasks: graph description translation, graph connectivity, and the shortest path problem. The results revealed that LLMs often fail in practical graph reasoning tasks, despite their theoretical capabilities. The study also highlighted the importance of balanced datasets and the influence of input context on LLM performance. Future research will focus on incorporating fine-tuning strategies to enhance the graph reasoning ability of LLMs.