Authors:
Paper:
https://arxiv.org/abs/2408.09523
Introduction
Background
The Transformer model, introduced by Vaswani et al. in 2017, has revolutionized the field of Natural Language Processing (NLP). Its architecture, characterized by self-attention mechanisms and the ability to handle long-range dependencies, has made it the backbone of numerous state-of-the-art systems in tasks such as machine translation, text summarization, and text generation. Despite its success, the Transformer model’s complexity poses significant challenges in terms of interpretability. Understanding how information flows and transforms within the multi-layered architecture of Transformers remains a daunting task.
Research Motivation and Objectives
Current interpretability methods for Transformer models often rely on discrete approximations or empirical observations, which fail to capture the continuous, dynamic processes of information flow within these models. This limitation constrains efforts to optimize model stability and performance, especially in high-stakes applications where reliability is critical. The objective of this research is to develop a unified mathematical model that integrates Partial Differential Equations (PDEs), Neural Information Flow Theory, and Information Bottleneck Theory to provide a comprehensive understanding of Transformer behavior. This model aims to enhance the interpretability of Transformers, optimize their architecture, and improve their stability and efficiency.
Contributions
This paper introduces a novel unified theoretical framework that integrates PDEs, Neural Information Flow Theory, and Information Bottleneck Theory to provide a continuous and rigorous explanation of Transformer models. The framework is validated through extensive experiments, demonstrating its potential to develop more interpretable, robust, and efficient AI systems.
Related Work
Explainability in Transformer Models
Transformer models have achieved significant success in NLP and computer vision but face challenges in explainability, particularly in fields like healthcare and law where transparency is critical. Recent research has developed explainability methods across three levels: input, processing, and output. Approaches such as Deep Taylor Decomposition and Layer-wise Relevance Propagation (LRP) have improved interpretability over traditional gradient-based methods. Alternatives to attention mechanisms, such as attention flow and attention rollout, have been proposed to better quantify token relevance.
Visualization and Analysis Tools
Tools like Ecco offer interactive ways to explore model behavior. In specific domains, explainability methods have been applied to tasks such as gene transcription analysis in genomics, sentiment analysis, and dynamic user representations in collaborative filtering. Visualizing patch interactions in vision transformers and tracking transformers with class and regression tokens have further expanded the understanding of attention mechanisms in these models.
Need for a Unified Framework
Despite these advancements, a unified framework for evaluating explainability methods is still needed. Current methods do not adequately address how information propagates through Transformer layers, limiting a deeper understanding of their internal mechanisms.
Research Methodology
Theoretical Foundation
Neural Information Flow Theory
Neural Information Flow Theory focuses on how information is transmitted and transformed across different layers of neural networks. It provides a framework for understanding how networks distill raw input into meaningful features, preserving relevant information while discarding unnecessary details.
Partial Differential Equations (PDEs)
PDEs are mathematical tools used to describe the continuous behavior of complex systems. In the analysis of Transformer models, PDEs allow us to model the flow of information as a continuous process, offering a nuanced perspective on how information evolves over time and across layers.
Information Bottleneck Theory
Information Bottleneck Theory addresses the trade-off between compressing input data and retaining information necessary for accurate predictions. It provides a framework for understanding how neural networks focus on relevant information while discarding redundancy.
Mathematical Model
PDE-Inspired Transformer Dynamics
The cornerstone of our model is a PDE-inspired formulation that captures the essence of information flow in Transformers. This formulation integrates diffusion terms, self-attention mechanisms, and nonlinear residual components into a single equation to capture the propagation and transformation of information within Transformers.
Information Bottleneck in Transformer Learning
The Information Bottleneck (IB) theory helps elucidate how the model balances retaining task-relevant information and compressing input representations. By integrating the IB theory into our PDE model, we can delve into the information dynamics during Transformer training.
Multi-Layer Information Flow in Transformers
Our multi-scale PDE framework captures the information processing within individual layers and simulates the interactions between layers, including the effects of residual connections and layer normalization. This enables hierarchical analysis, examining the specific behaviors of different layers and their contributions to the overall performance of the model.
Experimental Design
Summary of Experiments
To comprehensively evaluate the effectiveness of our proposed PDE framework in modeling and explaining Transformer behaviors, we conducted a series of five experiments:
| Experiment | Description |
|————————————|—————————————————————————–|
| Information Flow Visualization | Visualize and compare the information propagation patterns in PDE and Transformer models. |
| Attention Mechanism Analysis | Examine the attention distributions in both models to validate the PDE model’s ability to capture the essence of the Transformer’s attention mechanism. |
| Information Bottleneck Effect Validation | Investigate how information compression evolves with network depth in both PDE and Transformer models. |
| Gradient Flow Analysis | Analyze and compare the gradient propagation characteristics in PDE and Transformer architectures. |
| Perturbation Sensitivity Analysis | Assess the robustness of both models by introducing small disturbances to the input. |
Data and Model Description
We used datasets such as MNIST for image classification tasks and the 20 Newsgroups dataset for text classification. The models employed include a custom PDE model and a simplified Transformer model, both sharing similar architectures with multiple layers and hidden dimensions.
Results and Analysis
Information Flow Visualization
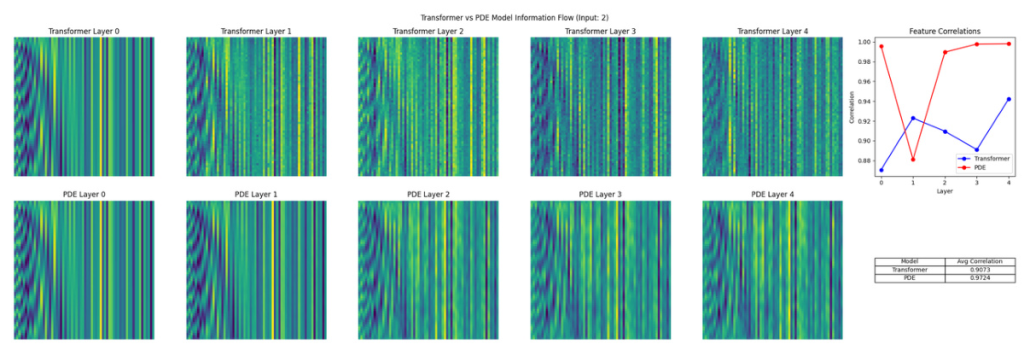
Introduction
The primary objective of this experiment is to observe and analyze the information flow patterns within a Transformer model by comparing them to those generated by a PDE model that simulates information flow.
Results and Analysis
The results of the visualization provide insights into how information flows through the layers of the Transformer model and how it is simulated by the PDE model. The PDE model effectively captures the information propagation and evolution process across layers, as indicated by the observable patterns in each layer’s heatmap.
Conclusion
The combined results from experiments demonstrate that the PDE model can effectively simulate the information flow characteristics of the Transformer model, including feature extraction, abstraction, compression, and focus.
Attention Mechanism Analysis
Introduction
This experiment aims to validate whether the attention component in the PDE model accurately reflects the attention mechanism of the Transformer model.
Results and Analysis
The high cosine similarity (0.9870) and low KL divergence (0.0144) indicate that the attention distributions of the PDE model closely match those of the Transformer model.
Conclusion
The experiment provides strong evidence that the PDE model accurately reflects the attention mechanism of the Transformer model.
Information Bottleneck Effect Validation
Introduction
This study aims to investigate the information compression process in Transformer models through the lens of Partial Differential Equations (PDE).
Results and Analysis
The overall trends observed in both the PDE and Transformer models align with the predictions of the Information Bottleneck (IB) theory, showing a general decline in mutual information over time.
Conclusion
The experiment provides robust evidence that the PDE model can effectively simulate the information flow characteristics of the Transformer model. However, notable differences in the degree and manner of information compression highlight that a simple PDE model may not fully capture the complex dynamics of Transformer models.
Gradient Flow Analysis
Introduction
This study aims to investigate the gradient propagation characteristics in Partial Differential Equation (PDE) models and Transformer architectures.
Results and Analysis
The gradient flow analysis reveals significant differences in the training dynamics of PDE and Transformer models.
Conclusion
The findings imply that PDE models can provide valuable insights into understanding and simulating the gradient flow observed in Transformer models.
Perturbation Sensitivity Analysis
Introduction
This study investigates the sensitivity of Partial Differential Equation (PDE) models and Transformer architectures to input perturbations.
Results and Analysis
The Transformer model demonstrates superior robustness to input perturbations compared to the PDE model.
Conclusion
The perturbation sensitivity analysis reveals crucial differences between PDE and Transformer models, highlighting an area where PDE frameworks need improvement to fully capture Transformer characteristics.
Overall Conclusion
This paper presents a novel approach to understanding Transformer architectures by modeling their information flow using Partial Differential Equations (PDEs). The PDE model successfully captures key aspects of Transformer behavior, including information propagation, attention mechanisms, and information compression. However, further refinements are necessary to fully bridge the gap between PDE models and Transformers, particularly in areas such as robustness to perturbations and handling of complex, non-linear transformations. Future work should focus on enhancing PDE models to better mimic the stability and robustness of Transformers while maintaining their interpretability and analytical advantages.