Authors:
Xiaosheng Li、Wenjie Xi、Jessica Lin
Paper:
https://arxiv.org/abs/2408.07956
Introduction
Neural networks are fundamental in machine learning, data mining, and artificial intelligence. Typically, these networks undergo a training phase where their parameters are tuned according to specific learning rules and data. This training often involves backpropagation to optimize an objective function. Once trained, these networks can be deployed for various tasks, including classification, clustering, and regression.
Time series clustering, which involves grouping time series instances into homogeneous groups, is a crucial and challenging task in time series data mining. It has applications in finance, biology, climate, medicine, and more. Existing methods for time series clustering often focus on a single aspect, such as shape or point-to-point distance, which can be suboptimal for certain data types.
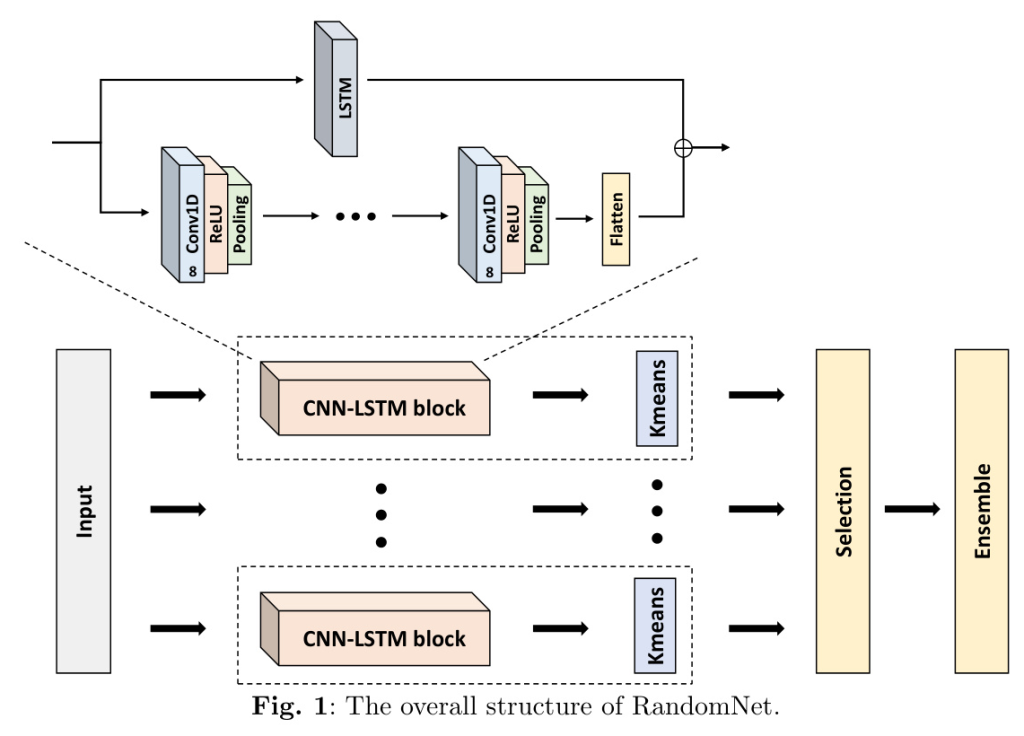
In this work, we introduce RandomNet, a novel method for time series clustering using untrained deep neural networks. Unlike conventional methods that adjust network weights using backpropagation, RandomNet utilizes different sets of random parameters to extract various representations of the data. These representations are clustered, and the results are ensembled to produce the final clustering. This approach ensures that data only needs to pass through the networks once, obviating the need for backpropagation, and provides a more efficient solution for time series clustering tasks.
Background and Related Work
Definitions and Notations
- Definition 1: A time series ( T = [t_1, t_2, \ldots, t_m] ) is an ordered sequence of real-value data points, where ( m ) is the length of the time series.
- Definition 2: Given a set of time series ( {T_i}_{i=1}^n ) and the number of clusters ( k ), the objective of time series clustering is to assign each time series instance ( T_i ) a group label ( c_j ), where ( j \in {1, \ldots, k} ). ( n ) is the number of instances in the dataset.
Related Work
Time series clustering methods can be categorized into four groups: raw-data-based methods, feature-based methods, deep-learning-based methods, and others.
- Raw-data-based methods: These methods directly apply classic clustering algorithms such as k-means on raw time series. They often struggle with scale-variance, phase-shifting, distortion, and noise in the data. Dynamic Time Warping (DTW) and its variants are popular distance measures used to address these challenges.
- Feature-based methods: These methods transform time series into flat, unordered features and then apply classic clustering algorithms. Examples include U-shapelets and Similarity PreservIng RepresentAtion Learning (SPIRAL).
- Deep-learning-based methods: Many methods in this category adopt the autoencoder architecture for clustering. Examples include Improved Deep Embedded Clustering (IDEC) and Deep Temporal Clustering (DTC).
- Other methods: These include methods like Symbolic Pattern Forest (SPF), which uses Symbolic Aggregate approXimation (SAX) to transform time series subsequences into symbolic patterns.
The Proposed Method
Architecture and Algorithm
RandomNet is structured with multiple branches, each containing a CNN-LSTM block designed to capture both spatial and temporal dependencies of time series, followed by k-means clustering. Each branch produces its own clustering, and a selection mechanism is used to remove skewed or deviant clusterings. The final clustering is obtained by ensembling the selected clusterings using the Hybrid Bipartite Graph Formulation (HBGF).
Algorithm 1: RandomNet
“`plaintext
Require: D: time series dataset; B: branch number; k: number of clusters; lr, ur: lower and upper bounds; sr: selection rate
Ensure: C: clustering assignment of D
1: function RandomNet(D, B, k, lr, ur, sr)
2: ClusteringSet ←empty
3: for i = 1 to B do
4: Randomize(CNN LSTM blocks)
5: Features ←CNN LSTM blocks(D)
6: Clustering ←Kmeans(Features)
7: ClusteringSet.add(Clustering)
8: end for
9: SelectedSet ←Selection(ClusteringSet, sr, lr, ur, B) // Algorithm 2
10: C ←Ensemble(SelectedSet) // Algorithm 3
11: return C
12: end function
“`
Effectiveness of RandomNet
RandomNet’s effectiveness is based on the idea that multiple random parameters can generate diverse data representations. Some representations are relevant to the clustering task, while others are not. By ensembling the clustering results derived from these diverse representations, the noise introduced by irrelevant representations tends to cancel out, while the connections provided by relevant representations are strengthened.
Theorem 1
Assume two instances, ( T_1 ) and ( T_2 ), are from the same class. If they reside within the same cluster under some relevant representations, then RandomNet assigns these two instances to the same cluster in the final output.
Theorem 2
Assume the ensemble size to be ( b ). Then, the lower bound of ( b ) needed to provide a good clustering is given by ( -2 \ln \alpha / \gamma^2 ), where ( \gamma ) represents the percentage of relevant representations and ( 1-\alpha ) is the confidence level.
Experimental Evaluation
Experimental Setup
To evaluate the effectiveness of RandomNet, we run the algorithm on all 128 datasets from the UCR time series archive. These datasets come from different disciplines with various characteristics. We compare RandomNet with several state-of-the-art methods, including kDBA, KSC, k-shape, SPIRAL, SPF, IDEC, DTC, ROCKET, MiniRocket, and MultiRocket.
Hyperparameter Analysis
We conduct a series of experiments to fine-tune and investigate the influence of hyperparameters on model performance. The hyperparameters include the number of branches, selection rate, and lower and upper bounds for cluster size.
Experimental Results
We compare RandomNet with k-means, kmeansE, ROCKET, MiniRocket, MultiRocket, and other state-of-the-art methods. RandomNet achieves the highest average Rand Index and average rank among all the baseline methods.
Ablation Study
We verify the effectiveness of each component in RandomNet by comparing the performance of the full RandomNet and its four variants on 108 UCR datasets. The results show that the full RandomNet is better than the four variants in average Rand Index and average rank.
Visualizing Clusters for Different Methods
We visualize the 2D embeddings of the Cylinder-Bell-Funnel (CBF) dataset using t-SNE and compare the cluster assignments by k-means, MiniRocket, and RandomNet with the true labels. RandomNet is able to identify the correct clusters more accurately than k-means and MiniRocket.
Testing the Time Complexity
We test the scalability and effectiveness of RandomNet by generating datasets of varying sizes and lengths. The results show that the average running time of RandomNet has a strong linear relationship with the number of instances and length of time series.
Analyzing Noise Sensitivity
We test the noise sensitivity of RandomNet using three different datasets injected with varying levels of random Gaussian noise. RandomNet exhibits strong resilience to noise and performs better than SPF.
Finding the Optimal Number of Clusters
We apply the Elbow Method to determine the optimal number of clusters for the CBF dataset. RandomNet can find an obvious “elbow” at ( k = 3 ), whereas it is hard to locate a clear “elbow” for k-means.
Conclusion and Future Work
In this paper, we introduced RandomNet, a novel method for time series clustering that utilizes deep neural networks with random parameters to extract diverse representations of the input time series for clustering. The selection mechanism and ensemble in the proposed method cancel irrelevant representations and strengthen relevant representations to provide reliable clustering. Extensive evaluations conducted across all 128 UCR datasets demonstrate competitive accuracy compared to state-of-the-art methods, as well as superior efficiency.
Future research directions may involve integrating more complex or domain-specific network structures into our method. Additionally, incorporating some level of training into the framework could potentially improve performance. We will also explore the potential of applying our method to multivariate time series or other data types, such as image data.