Authors:
Homayoun Honari、Amir Mehdi Soufi Enayati、Mehran Ghafarian Tamizi、Homayoun Najjaran
Paper:
https://arxiv.org/abs/2408.07962
Introduction
Reinforcement Learning (RL) has shown significant success in various domains such as energy systems, video games, and robotics. However, deploying RL in real-world scenarios is challenging due to the extensive trial-and-error nature of the learning process, which can lead to unsafe states and potential damage to the system. Safe Reinforcement Learning (Safe RL) aims to address this issue by optimizing policies that comply with predefined constraints, typically using the Lagrangian method. However, the real-world deployment of Lagrangian-based safe RL is hindered by the need for precise threshold tuning, which can lead to suboptimal policy convergence if not done correctly.
To address these challenges, the authors propose a unified Lagrangian-based model-free architecture called Meta Soft Actor-Critic Lagrangian (Meta SAC-Lag). This method uses meta-gradient optimization to automatically update safety-related hyperparameters, thereby minimizing the need for manual tuning. The proposed method is evaluated in five simulated environments and a real-world robotic task, demonstrating its capability to achieve better or competitive results compared to baseline algorithms.
Related Work
The theoretical foundation of safe RL is the Constrained Markov Decision Process (CMDP), which has been widely studied and typically solved using Lagrangian methods. Various approaches have been proposed to optimize the Lagrangian multiplier and policy, including risk-sensitive policy optimization, PID control, and dual gradient descent. Metagradient optimization has also been explored for hyperparameter tuning in RL, but its application in constrained RL paradigms is limited.
Other approaches to safe RL include training recovery policies, model-based RL with safety guarantees, and using Lyapunov functions to ensure safety during training. Despite significant progress, there remains a gap in readily deployable safe RL agents for industrial contexts. The authors aim to use metagradient optimization for self-tuning of the safety threshold, minimizing the need for manual tuning and improving performance.
Background
Constrained Markov Decision Process (CMDP)
A CMDP is defined by the tuple , where S is the state space, A is the action space, P is the transition function, r is the reward function, c is the constraint indicator function, γr and γc are discount factors for reward and safety critics, respectively, and ρ0 is the initial state distribution. The goal is to find a policy π that maximizes the expected return while satisfying the constraints.
Soft Actor-Critic (SAC)
SAC optimizes a stochastic policy in an off-policy manner using two neural networks: one for estimating the Q-function (critic) and another for policy updates (actor). SAC incorporates entropy regularization to balance exploration and exploitation. The critic network is trained using the mean squared error (MSE) loss, while the policy is optimized by maximizing the expected entropy and minimizing the Q-value.
Method
Metagradient Optimization
Metagradient optimization is used to optimize hyperparameters that are not part of the main loss function. The learnable system variables are parameterized as θ, and the hyperparameters η are updated based on the gradients of the meta-objective J’ with respect to θ’.
SAC-Lagrangian
In the Lagrangian version of SAC, the policy is optimized to maximize the reward while satisfying the safety constraints. The optimization process is formulated as a Lagrangian loss, and the Lagrange multiplier ν is updated accordingly.
Meta SAC-Lag
Meta SAC-Lag splits the parameters into inner and outer parameters and updates them sequentially. The inner parameters (ν and ϕ) are updated based on the Lagrangian loss, while the outer parameters (ε and α) are updated based on their respective objective functions. The objective function for ε is designed to improve the overall performance of the policy, while the objective function for α ensures safety compliance.
Implementation Details
Meta SAC-Lag uses three replay buffers for training: the main replay buffer D, the safety replay buffer Ds, and the initial state buffer D0. The critic networks and inner parameters are trained using samples from D, while the meta-parameters ε and α are trained using resampled batches from D and D0, respectively. The algorithm uses RMSProp for higher-order gradient calculations to ensure numerical stability.
Experiments
Test Benchmarks and Baselines
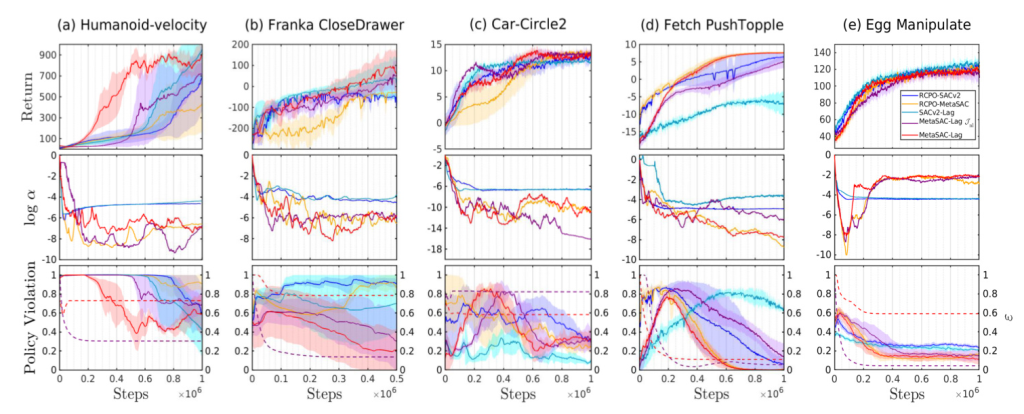
The performance of Meta SAC-Lag is evaluated in five simulated robotic environments with different themes: locomotion, obstacle avoidance, robotic manipulation, and dexterous manipulation. The baseline algorithms used for comparison are SACv2-Lag, RCPO-SACv2, RCPO-MetaSAC, and Meta SAC-Lag with a nonlinear objective function for ε.
Simulation Results
The simulation results show that Meta SAC-Lag provides automated tuning of safety-related hyperparameters, resulting in lower constraint violations and higher or comparable returns compared to baseline algorithms. The fast convergence of ε provides stable optimization, and the optimization outcomes demonstrate that Meta SAC-Lag excels across various tasks with minimal hyperparameter tuning.
Real-World Deployment
The deployability of Meta SAC-Lag is tested in a real-world robotic task called Pour Coffee, where a Kinova Gen3 robot is tasked with pouring coffee into a cup without spillage. The results show that Meta SAC-Lag can achieve comparable performance to simulation-trained models while minimizing effort and ensuring safety.
Conclusions
The paper presents Meta SAC-Lag, a novel model-free architecture for safe RL that uses metagradient optimization to automatically adjust safety-related hyperparameters. The algorithm is evaluated in five simulated environments and a real-world robotic task, demonstrating its capability to achieve better or competitive results compared to baseline algorithms. The proposed method reduces the reliance on manual tuning and heuristic implementation of safety, making it suitable for real-world safety-sensitive applications.