Authors:

Yuanjian Xu、Anxian Liu、Jianing Hao、Zhenzhuo Li、Shichang Meng、Guang Zhang

Paper:

https://arxiv.org/abs/2408.10111

Unveiling Financial Time Series Regularities with PLUTUS: A Deep Dive

Introduction

Financial time series analysis is a cornerstone of modern finance and economics, underpinning decision-making processes across various sectors. However, the inherent complexities of financial data—characterized by non-linearity, non-stationarity, heteroskedasticity, and high noise levels—pose significant challenges for traditional modeling techniques. These complexities often lead to volatile data that lack consistent patterns, making it difficult for conventional statistical methods and even advanced deep learning models to achieve high predictive accuracy.

Inspired by the success of large language models (LLMs) in natural language processing (NLP), the authors introduce PLUTUS, a well-pretrained large unified transformer-based model designed to unveil regularities in financial time series data. By leveraging techniques such as contrastive learning, autoencoders, and multi-scale temporal attention mechanisms, PLUTUS aims to address the unique challenges of financial time series modeling.

Related Work

Challenges in Financial Time Series Modeling

Financial time series data are influenced by a myriad of factors, including economic conditions, political events, and market speculations. Traditional models often struggle to capture the intricate dependencies and sudden shifts inherent in such data, leading to poor generalization and predictive performance. The high noise levels further exacerbate the risk of overfitting to irrelevant patterns.

Success of Large Language Models

Large language models like GPT-4 have demonstrated remarkable abilities in understanding and generating coherent text by learning from vast amounts of sequential data. Given the sequential nature of both NLP and financial data, there is a compelling opportunity to apply similar paradigms to financial time series modeling.

Tokenization and Embedding Techniques

Recent advancements have shown that tokenizing time series into patches, similar to embedding layers in NLP, can effectively segment the data into meaningful components. Establishing a one-to-one mapping between these raw financial data patches and their corresponding embeddings is crucial for efficient model operation in the embedding space.

Research Methodology

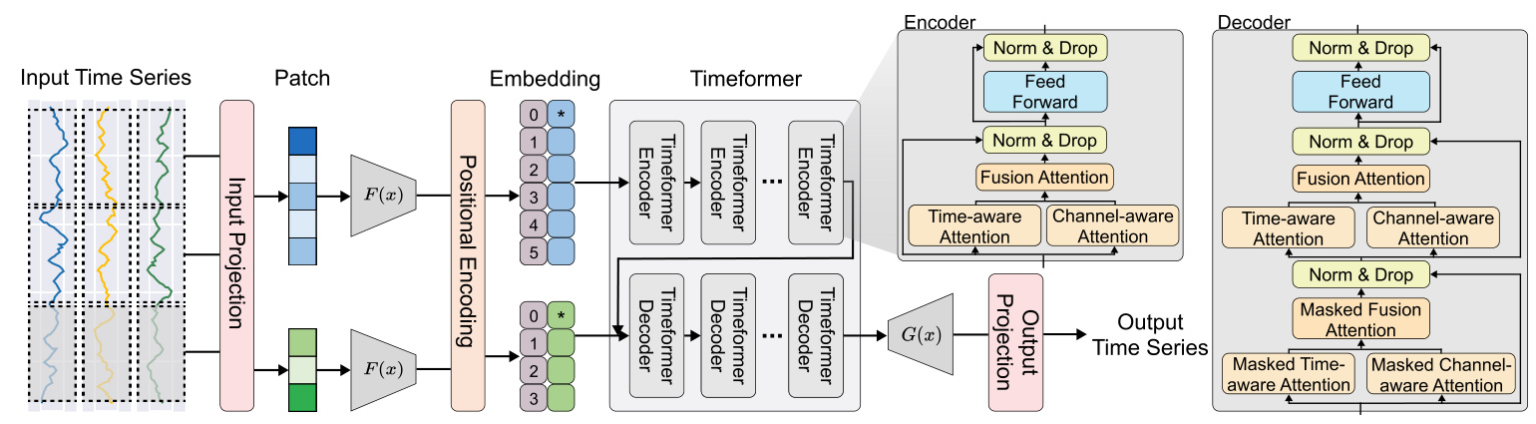
PLUTUS Architecture

PLUTUS employs an encoder-decoder architecture, which has proven effective in handling high-noise time series samples. The model consists of several key components:

1. Invertible Embedding Module: This module uses contrastive learning and autoencoder techniques to establish an approximate one-to-one mapping between raw time series data and patch embeddings.
2. TimeFormer: An encoder-decoder architecture that incorporates multi-scale temporal attention mechanisms to capture features across both variable and temporal dimensions.
3. Multi-Scale Temporal Attention Mechanisms: These mechanisms effectively segment time series data into meaningful patches and improve the mapping between raw data and patch embeddings.

Invertible Embedding Module

The invertible embedding module divides the time series into patches and generates positive and negative samples by adding small noise and flipping the patches along the time axis, respectively. The embeddings are optimized using the InfoNCE loss, which encourages similar patches to have similar embeddings while pushing dissimilar patches apart. An inverse embed layer maps the embeddings back to the original patch dimensions, minimizing the Mean Squared Error (MSE) between the original and reconstructed patches.

TimeFormer

TimeFormer processes the input tensor through time-aware attention, channel-aware attention, and fusion attention. The attention scores are calculated using trainable matrices, and masks are applied to prevent the model from exposing future time information. The intermediate attention representation is obtained by combining the time-aware and channel-aware attention outputs through a weighted sum.

Training Process

The training process for PLUTUS involves two key phases:

1. Training the Invertible Embedding Module: This phase focuses on mapping raw time series patches into a latent space and reconstructing them back into the original space using contrastive and reconstruction losses.
2. Multi-Task Pre-Training: The model undergoes multi-task pre-training focused on the TimeFormer Encoder and Decoder. This phase involves training the model on a range of tasks with varying input-output time series lengths, ensuring accurate future predictions across different tasks.

Experimental Design

Financial Data for Pretraining

Curating large-scale financial time series datasets presents significant challenges. The Financial Time Series Dataset (FTSD) encompasses 19 sub-datasets representing a broad range of aspects within the financial domain. FTSD covers various sampling frequencies, from yearly data to more granular intervals like seconds, with total observations exceeding 100 billion.

Benchmarks and Overall Comparison

PLUTUS is evaluated on three fundamental tasks in financial time series analysis: long-term forecasting, imputation, and portfolio management. The model’s performance is compared with state-of-the-art models across different backbone architectures. The downstream dataset is derived from the ‘CRSP daily price 1984-2024’ sub-dataset, which includes 20 variables with 203,860 observations.

Long-Term Forecasting

In long-term financial time series forecasting tasks, PLUTUS consistently outperforms other models across all prediction lengths, with an average reduction of 60% in MSE and 15% in MAE. This suggests that pre-training on large-scale financial time series data has enabled PLUTUS to effectively capture unique patterns within financial data.

Imputation

Imputation is another critical task in time series analysis. PLUTUS consistently achieves the lowest MSE, particularly at lower masking ratios, with a 39.74% reduction at 0.125. This highlights the model’s strength in minimizing significant errors and its applicability in scenarios where reducing large prediction errors is crucial.

Portfolio Management

In classic portfolio management scenarios, portfolios based on PLUTUS predictions demonstrate strong performance. The model achieves higher average daily returns and lower maximum drawdowns compared to other investment strategies, indicating its potential to reduce risks in financial decision-making.

Results and Analysis

Ablation Study

The ablation study demonstrates the significant contributions of each module to the performance of the PLUTUS model. The encoder, decoder, and various attention mechanisms play crucial roles in capturing temporal dependencies, reducing noise, and aligning raw patch time series data with the latent vector space.

Exploration of Embedding Space

The alignment and uniformity metrics provide deeper insights into the invertible embedding module. Smaller patches and larger embedding dimensions facilitate a more uniform distribution of samples across the embedding space, enhancing the model’s ability to extract meaningful patterns from complex and noisy financial data.

Scaling Experiments

PLUTUS is provided in three sizes—small, base, and large. The results demonstrate a clear improvement in both prediction and imputation tasks as the model size increases, underscoring the importance of model size in capturing complex financial time series patterns.

Case Study

A case study illustrates the significant advantages of PLUTUS in predicting the next 196 time steps. The model tracks the true value curve more closely and excels in capturing and anticipating time series trends, making it more adaptive and accurate in financial time series forecasting tasks.

Overall Conclusion

PLUTUS represents a significant advancement in financial time series modeling, leveraging the strengths of large language models and advanced deep learning techniques. By addressing the unique challenges of financial data, PLUTUS achieves state-of-the-art performance across various downstream tasks, demonstrating powerful transferability and establishing a robust foundational model for finance. The research provides comprehensive technical guidance for pre-training financial time series data, establishing a new paradigm for financial time series modeling.