Authors:
Emanuele De Angelis、Maurizio Proietti、Francesca Toni
Paper:
https://arxiv.org/abs/2408.10126
Introduction
Assumption-Based Argumentation (ABA) is a structured form of argumentation that has been widely recognized for its ability to unify various non-monotonic reasoning formalisms, including logic programming. ABA frameworks allow for the representation of defeasible knowledge, which is subject to argumentative debate. Traditionally, these frameworks are provided upfront, but this paper addresses the challenge of automating their learning from background knowledge and examples. Specifically, the focus is on brave reasoning under stable extensions for ABA, introducing a novel algorithm that leverages Answer Set Programming (ASP) for implementation.
Related Work
Several forms of ABA Learning have been explored in previous studies. The work in [21] is closely related, relying on transformation rules but focusing on cautious ABA Learning. In contrast, this paper introduces a novel formulation of brave ABA Learning. Other related works include [6], which also uses ASP for implementing ABA Learning, and [28], which focuses on cautious ABA Learning using Python. The approach in this paper is distinct in its use of brave reasoning and its reliance on ASP for supporting the learning algorithmically.
ABA can be seen as performing abductive reasoning, and other approaches combine abductive and inductive learning [22]. However, these do not learn ABA frameworks. Additionally, methods for learning non-monotonic formalisms, such as [14, 24, 27], either do not use ASP or focus on stratified logic programs with a unique stable model. Amongst these, ILASP [15] can perform both brave and cautious induction of ASP programs, whereas [25] performs cautious induction, and [26] can perform brave induction in ASP.
Research Methodology
Answer Set Programs
ASP consists of rules of the form:
p :- q1, ..., qk, not qk+1, ..., not qn
where p, q1, …, qn are atoms, k ≥ 0, n ≥ 0, and not denotes negation as failure. An atom p is a brave consequence of P if there exists an answer set A of P such that p ∈ A.
Assumption-Based Argumentation (ABA)
An ABA framework is a tuple ⟨L, R, A, ⟩ where:
– ⟨L, R⟩ is a deductive system with L as a language and R as a set of inference rules.
– A is a non-empty set of assumptions.
– is a total mapping from A into L, where a is the contrary of a.
The semantics of flat ABA frameworks is given by “acceptable” extensions, i.e., sets of arguments able to “defend” themselves against attacks. A stable extension is a set of arguments that is conflict-free and attacks all arguments it does not contain.
Experimental Design
Brave ABA Learning under Stable Extensions
The goal of brave ABA Learning is to construct an ABA framework ⟨R′, A′, ′⟩ such that:
1. For all positive examples e ∈ E+, ⟨R′, A′, ′⟩ | =∆ e.
2. For all negative examples e ∈ E−, ⟨R′, A′, ′⟩ ̸| =∆ e.
Transformation Rules
The learning process is guided by transformation rules:
1. Rote Learning: Adds facts from positive examples or facts for contraries of assumptions.
2. Folding: Generalizes a rule by replacing some atoms in its body with their consequence using a rule in R.
3. Assumption Introduction: Adds an assumption to the body of a rule to make it defeasible.
4. Fact Subsumption: Removes a rule if the ABA framework still bravely entails the examples without it.
Algorithm ASP-ABAlearnB
The ASP-ABAlearnB algorithm consists of two procedures:
1. RoLe: Applies Rote Learning to add a minimal set of facts to the background knowledge.
2. Gen: Transforms the ABA framework into an intensional solution by applying Folding, Assumption Introduction, and Fact Subsumption.
Results and Analysis
Implementation and Experiments
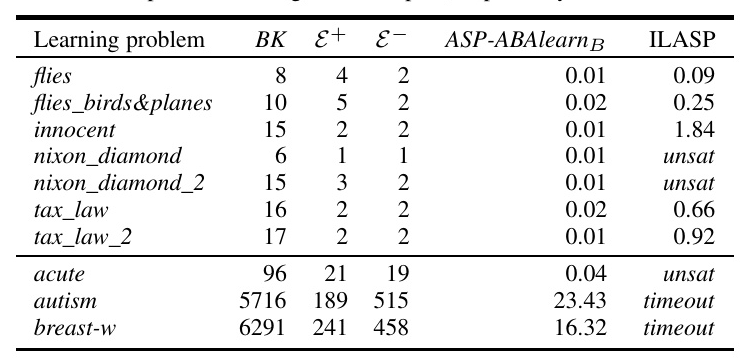
A proof-of-concept implementation of the ASP-ABAlearnB strategy was realized using SWI-Prolog and the Clingo ASP solver. The experimental evaluation was conducted on a benchmark set of classic learning problems and larger datasets. The results were compared with ILASP, a state-of-the-art learner for ASP programs.
The table shows that ASP-ABAlearnB performed well on various learning problems, often outperforming ILASP, especially in cases where ILASP was unable to learn a solution within the timeout.
Overall Conclusion
This paper presents a novel approach for learning ABA frameworks based on transformation rules and implemented via ASP. The approach is shown to be effective for brave reasoning under stable extensions, with soundness and termination properties established under suitable conditions. The experimental results demonstrate the potential of the ASP-ABAlearnB algorithm in solving non-trivial learning problems, highlighting its advantages over existing methods like ILASP.
Future work includes refining the implementation, performing a more thorough experimental comparison with other non-monotonic ILP systems, and extending the approach to different logics and semantics. The ability to learn non-flat ABA frameworks and integrate with tools beyond ASP solvers is also a potential direction for further research.