Authors:
Elena Umili、Francesco Argenziano、Roberto Capobianco
Paper:
https://arxiv.org/abs/2408.08677
Neural Reward Machines: A Neurosymbolic Framework for Non-Markovian Reinforcement Learning
Introduction
Reinforcement Learning (RL) tasks are traditionally modeled as Markovian Decision Processes (MDPs), where task feedback depends solely on the last state and action. However, many decision problems are inherently non-Markovian or temporally extended, requiring agents to consider the entire history of state-action pairs to act rationally. Current research addresses non-Markovianity by expanding the state space with features that encode the environment history and solving the augmented-state problem with established RL algorithms. This paper introduces Neural Reward Machines (NRMs), an automata-based neurosymbolic framework that combines RL with semi-supervised symbol grounding (SSSG) to handle non-symbolic non-Markovian RL domains without prior knowledge of the symbol grounding (SG) function.
Related Works
Non-Markovian Reinforcement Learning with Temporal Specifications
Temporal logic formalisms are widely used in RL to specify non-Markovian tasks. Most works assume that boolean symbols used in the task formulation are perfectly observable in the environment, making them applicable only in symbolic-state environments or when a perfect mapping between the environment state and a symbolic interpretation is known. Some works assume an imperfect SG function, which sometimes makes mistakes in predicting symbols from states or predicts a set of probabilistic beliefs over the symbol set instead of a boolean interpretation. However, these works do not address the problem of learning the SG function.
Semisupervised Symbol Grounding
SSSG approaches the SG problem by assuming some prior symbolic logical knowledge and a set of raw data annotated with the output of the knowledge. SSSG is tackled mainly with two families of methods: embedding a continuous relaxation of the available knowledge in a larger neural network system or maintaining a crisp boolean representation of the logical knowledge and using logic abduction to correct the current SG function.
Groundability and Reasoning Shortcuts
Reasoning shortcuts (RS) are mappings that maintain consistency between knowledge and data but are not the intended solution. Ungroundability is a property solely dependent on the logical knowledge and not on the data or the SG function. This paper introduces Unremovable Reasoning Shortcuts (URS), which are RSs identifiable when considering all possible observations.
Background
Moore Machines
A Moore machine is a tuple consisting of a finite alphabet of input propositional symbols, a finite set of states, a finite set of output symbols, an initial state, a transition function, and an output function. The transition and output functions over strings are defined recursively.
Non-Markovian Reward Decision Processes and Reward Machines
In RL, the agent-environment interaction is generally modeled as an MDP. However, many natural tasks are non-Markovian. Non-Markovian Reward Decision Processes (NMRDP) focus on non-Markovian reward functions. Reward Machines (RMs) are an automata-based representation of non-Markovian reward functions, specifying temporally extended rewards over propositions while exposing the compositional reward structure to the learning agent.
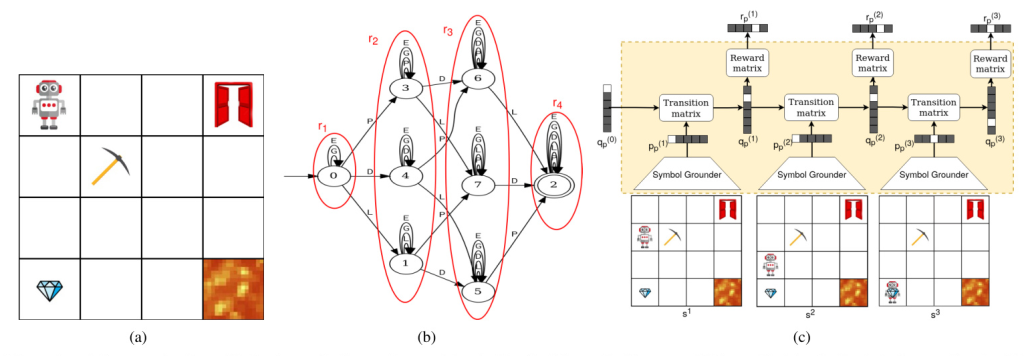
Example: Image-Based Minecraft-Like Environment
Consider an environment consisting of a grid world with different items: a pickaxe, a gem, a door, and a lava-cell. The task is to reach at least once the pickaxe, the lava, and the door cells in any order. This task can be represented with a Moore Machine defined in terms of symbols for each item and an empty cell. The agent must learn to navigate the grid to satisfy the task, receiving an image as the state representation, which is not Markovian.
Neural Reward Machines
Definition and Notations
A Neural Reward Machine (NRM) is defined as a tuple consisting of the set of environment states, a finite set of symbols, a finite set of states, a finite set of rewards, an initial state, a machine transition probability function, a reward probability function, and a symbol grounding probability function. Unlike RMs, NRMs can process non-symbolic input sequences, maintaining a link with the symbolic representation through the symbol grounding function.
Implementation
NRMs are implemented using neural networks, employing probabilistic relaxations and matrix representations of functions. The symbol grounding function can be implemented with any neural network featuring softmax activation on the output layer. The recurrent module is defined as a parametric probabilistic Moore Machine (PMM), closely related to Recurrent Neural Networks (RNNs). The NRM implementation with parametric models is represented as follows:
markdown
p(t) p = sg(s(t); θsg)
q(t) p = ∑(i=1 to |P|) p(t) p [i](q(t−1) p (softmaxτ(Mt, τ))[i])
r(t) p = q(t) p softmaxτ(Mr, τ)
Reasoning and Learning with NRM
NRMs allow both reasoning and learning, with different configurations of prior knowledge on the NRM parameters and the possibility to observe rewards in the environment. Pure reasoning requires prior knowledge of all NRM parameters and does not require reward feedback. Pure learning involves learning the NRM modules entirely from data by minimizing the cross-entropy loss between the predicted and ground-truth rewards. Learning and reasoning integration involves training the missing modules to align with both prior knowledge and data.
Exploiting NRMs for Non-Markovian RL
In this setting, the agent learns to perform a temporally extended task by optimizing a non-Markovian reward signal. The agent interacts with the environment, receiving a new state and reward in response. The NRM framework exploits both symbolic knowledge and data from the environment by interleaving RL and semi-supervised symbol grounding. The parameters of the grounder are initialized with random weights, and the machine state sequence is calculated with the NRM, augmenting each environment state with the predicted machine state. The interaction is led by an RL algorithm running on the augmented state, and the symbol grounder is updated at regular intervals to minimize the loss.
Groundability Analysis of Temporal Specifications
SG and RL are closely intertwined, with SG relying on RL for data collection and RL relying on SG for an estimated representation of the automaton’s state. Ungroundability is a property of a symbol in the formula, independent of the supporting dataset or the SG function. This paper introduces an algorithm for identifying URS, leveraging stopping criteria to enhance speed.
Experiments
Application
NRMs are tested on two types of environments inspired by the Minecraft videogame: a map environment with a 2D vector state and an image environment with a 64x64x3 pixel image state. The non-Markovian reward is expressed as an LTLf formula, transformed into a DFA and a Moore Machine. Tasks of increasing difficulty are constructed using patterns of formulas popular in non-Markovian RL.
Comparisons
NRMs are compared with RNNs and RMs, using Advantage Actor-Critic (A2C) as the RL algorithm. The performance of NRMs falls between that of RNNs and RMs, closely resembling the latter across various experimental configurations.
Groundability Analysis
The number of URS identified running the algorithm on selected tasks confirms that as the tasks’ difficulty increases, the number of URS decreases, resulting in a reduction in groundability difficulty. The algorithm executes a thousand times faster than the brute-force implementation.
Conclusions and Future Work
Neural Reward Machines provide a versatile and applicable neurosymbolic framework for non-Markovian rewards in non-symbolic-state environments. NRMs effectively leverage incomplete prior knowledge to outperform Deep RL methods, achieving nearly equivalent rewards to RMs. Future research will explore other reasoning-learning scenarios, such as the integration of automata learning with RL.