Authors:
Coşku Can Horuz、Matthias Karlbauer、Timothy Praditia、Sergey Oladyshkin、Wolfgang Nowak、Sebastian Otte
Paper:
https://arxiv.org/abs/2408.10649
Introduction
Background
Spatiotemporal partial differential equations (PDEs) are fundamental in modeling various scientific and engineering phenomena. These equations describe how physical quantities evolve over space and time, making them crucial for understanding complex systems such as fluid dynamics, heat transfer, and wave propagation. Traditional approaches to solving PDEs have relied heavily on numerical methods grounded in physics. However, the advent of machine learning (ML) has introduced new possibilities for enhancing these models.
Problem Statement
Despite the advancements in both physics-based and machine learning models, there remains a gap in effectively integrating these approaches to uncover latent structures in data. This study focuses on the finite volume neural network (FINN), a hybrid model that combines the finite volume method (FVM) with deep learning. Specifically, the research investigates FINN’s ability to reconstruct underwater topography using the shallow-water equations (SWE), which model wave dynamics in coastal regions.
Related Work
Physics-Aware Machine Learning Models
Physics-aware machine learning models have shown promise in outperforming pure ML models by incorporating physical principles. These models have been applied successfully across various domains, demonstrating enhanced performance and interpretability. However, they often struggle to explicitly incorporate physical equations and infer underlying physical structures from data.
Finite Volume Neural Network (FINN)
FINN represents a significant advancement in this field by embedding physical principles within the FVM structure. This hybrid approach allows FINN to model PDEs in a mathematically compositional manner, directly incorporating boundary conditions and inferring hidden information from data. Previous studies have demonstrated FINN’s capability to handle various PDEs, making it a suitable candidate for this research.
Comparative Models
The study compares FINN with two other models: DISTANA and PhyDNet. DISTANA is a pure ML model designed for spatiotemporal data, while PhyDNet is a physics-aware encoder-decoder model. Both models serve as baselines to evaluate FINN’s performance in reconstructing underwater topography.
Research Methodology
FINN Architecture
FINN combines the finite volume method (FVM) with deep neural networks to solve PDEs. The FVM discretizes continuous PDEs into algebraic equations over control volumes, enforcing conservation laws. FINN’s architecture includes modules that approximate spatial derivatives and other physical quantities using linear layers. These modules are combined to form a system of ordinary differential equations (ODEs), which are solved iteratively to predict the next time step.
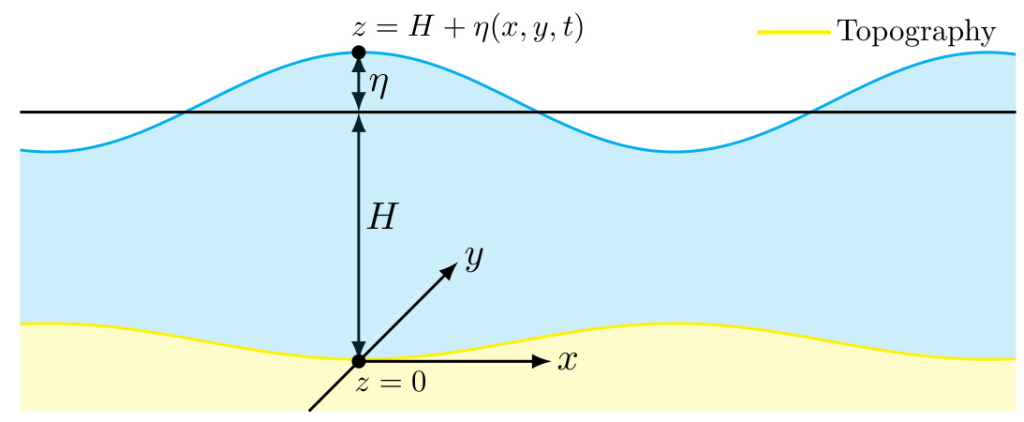
Shallow-Water Equations (SWE)
The shallow-water equations (SWE) are a set of PDEs that model wave dynamics in shallow water. These equations are derived from the principles of continuity and momentum conservation. In this study, the nonlinear form of the continuity equation is considered, while the momentum equations are taken to be linear. The goal is to reconstruct the underwater topography (H) from the displacement of the free surface (η).
Model Adaptation
To adapt FINN for solving SWE, significant modifications were made to its architecture. The adaptation involves sequentially computing the unknown state η and the velocities u and v. The initial condition η(t=0) is fed into the model, and the resulting velocities are used to estimate the time derivatives of η at the next time step. This process is repeated iteratively to reconstruct the topography.
Experimental Design
Data Preparation
The training and inference datasets consist of various topographies over a 1000 km² area. The training topography is smooth and has a large depth range, while the inference topography is more non-linear and bumpy. Different sequences with varying initial conditions are generated to expose the models to a wide range of topographies.
Training and Inference
The models are trained using a multi-topography scheme, where different sequences with varying topographies are fed into the model. This approach allows the models to learn the effect of different topographies and improve their inference capabilities. During inference, the models are tasked with reconstructing a particular topography from data, using multiple sequences to avoid overfitting to artifacts.
Evaluation Metrics
The performance of the models is evaluated using various metrics, including training error, inference error, test error, and reconstruction errors. The reconstruction errors are computed as the root mean squared error between the inferred and actual topographies, with separate metrics for the full domain and the inner domain (excluding boundaries).
Results and Analysis
Model Performance
The results indicate that FINN outperforms both DISTANA and PhyDNet in reconstructing underwater topography. FINN achieves lower inference and test errors, demonstrating its ability to accurately model the SWE and infer the underlying topographical structure. DISTANA also performs well but struggles with boundary conditions, leading to higher reconstruction errors. PhyDNet, despite its physics-aware design, fails to produce meaningful reconstructions due to overfitting and computational complexity.
Visualization of Results
The most accurate topography reconstructions for each model are visualized to provide a clearer understanding of their performance. FINN’s reconstructions closely match the actual topography, while DISTANA and PhyDNet exhibit significant deviations, particularly along the edges.
Error Analysis
The difference between training and test errors for FINN is attributed to the distinct topographies in the training and testing datasets. The training set has a larger error regime due to its wider range of topography values, leading to higher training errors compared to the test set.
Overall Conclusion
Summary
This study demonstrates the potential of FINN in accurately inferring underwater topography from wave dynamics modeled by the shallow-water equations. FINN’s hybrid architecture, which integrates the finite volume method with deep learning, allows it to effectively handle boundary conditions and infer hidden structures in data. The results highlight FINN’s superiority over both pure ML and other physics-aware models in this task.
Future Directions
The findings open up new avenues for applying FINN to a broader range of spatiotemporal problems characterized by advection-diffusion processes. Future research could explore the application of FINN to real-world scenarios, such as modeling wave dynamics in coastal regions and reconstructing coastal underwater topography. Additionally, integrating more complex versions of the Navier-Stokes equations into FINN’s framework could further enhance its utility and broaden its application in understanding and predicting natural phenomena.