Authors:
Litian Huang、Xinguo Yu、Feng Xiong、Bin He、Shengbing Tang、Jiawen Fu
Paper:
https://arxiv.org/abs/2408.10592
Introduction
Algebra Problems with Geometry Diagrams (APGDs) present a unique challenge in educational contexts, requiring solvers to interpret both textual descriptions and geometric diagrams. This task necessitates a combined understanding of algebraic and geometric principles. The complexity arises from the need to apply geometric theorems and manage implicit information within diagrams, which are not always explicitly stated. Addressing these challenges is crucial for developing intelligent educational tools and advancing automated reasoning systems.
Existing techniques for solving APGDs are divided into two primary categories: neural methods and symbolic methods. Neural methods utilize neural networks to process multimodal inputs, integrating textual descriptions and geometry diagrams into a unified sequence for generating solutions. Symbolic methods focus on extracting and interpreting geometric relations from APGDs, constructing symbolic representations essential for applying geometric theorems and algebraic operations.
Despite the progress made by existing methods, both neural and symbolic methods have significant limitations. Neural methods often struggle with accurately interpreting mathematical diagrams and exhibit vulnerabilities in mathematical reasoning. Symbolic methods, while providing mathematical rigor, are prone to generating redundant steps, resulting in longer solution times and decreased efficiency. To address these limitations, this paper proposes a novel method called Hologram Reasoning (HGR) for solving APGDs.
Related Work
Methods of Solving APGDs
Recent advancements in solving APGDs have primarily focused on two categories: neural methods and symbolic methods.
-
Neural Methods: These methods leverage neural networks to integrate textual and diagrammatic inputs, producing solutions through cross-modal representations. They excel at processing multimodal data, creating a unified framework for processing text and diagrams. However, they often struggle with accurately capturing the detailed aspects of diagrams and maintaining logical coherence in the solutions.
-
Symbolic Methods: These methods first parse the textual descriptions and geometric diagrams to extract structured representations, then utilize these representations to apply predefined theorems and rules for problem-solving. They provide a clear rule-based framework for interpreting the geometric relations within APGDs, making them highly interpretable and ensuring mathematical rigor. However, symbolic methods are often constrained by their reliance on rigid symbolic systems based on formal language, limiting their applicability.
Integration of Neural and Symbolic Methods
To address the limitations of neural and traditional symbolic methods, the integration of symbolic and neural methods has led to significant advancements in solving APGDs. Integrated methods leverage the strengths of both symbolic and neural methods, offering more comprehensive, efficient, and interpretable solutions for APGDs.
Research Methodology
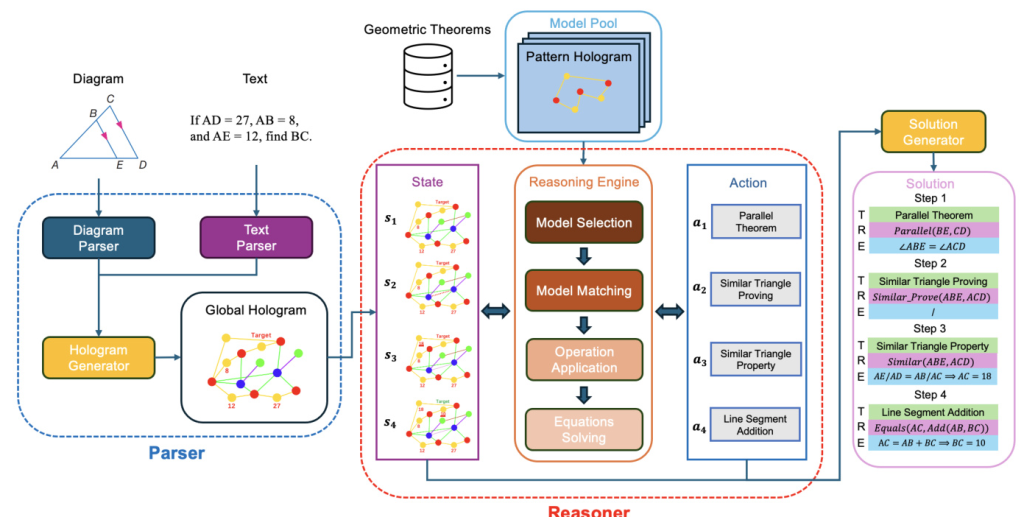
The HGR method for solving APGDs consists of several components, as depicted in Figure 2. The definition of the hologram and each HGR component are introduced separately.
Hologram
Inspired by the Geometry Logic Graph (GLG) used in GeoDRL, the hologram serves as the foundation for the reasoning process and solution generation. The hologram is a heterogeneous attributed graph denoted as ( G = (V, E, A, \hat{A}) ), where:
- Vertices (V): Represent various geometric primitives, including points, lines, angles, arcs, circles, and polygons.
- Edges (E): Represent the geometric relations between the primitives, including adjacency, incidence, parallelism, perpendicularity, similarity, and congruence.
- Mathematical Attributes (A): Include measurable properties such as lengths of lines, measures of angles, and areas of polygons.
- Visual Attributes ((\hat{A})): Include properties of geometric primitives calculated from the diagram image, such as point positions, visual lengths, and angles.
Parser
The parser of HGR plays a critical role in converting raw problem inputs into structured data that can be used for reasoning. The parser consists of three parts: text parser, diagram parser, and hologram generator.
- Text Parser: Interprets the problem text into a set of logical expressions in formal language.
- Diagram Parser: Analyzes and interprets the geometry diagram provided in the problem.
- Hologram Generator: Converts the parsed structured data into a hologram.
Graph Model Construction
In HGR, graph models play a crucial role in the reasoning process, encapsulating geometric configurations and relations. These models are divided into two primary types: Proving Models and Property Models. The collection of these models forms the model pool.
- Proving Models: Used to verify geometric theorems and update the global hologram.
- Property Models: Used to generate algebraic equations based on geometric properties.
Reasoner
The reasoner in HGR iteratively applies geometric theorems to the global hologram until the final solution is reached. The reasoning process involves several key steps:
- Proving Model Matching: Matching the proving model with the global hologram.
- Graph Expansion: Updating the global hologram with new vertices or edges.
- Property Model Matching: Matching the property model with the global hologram.
- Equations Derivation: Deriving equations based on the matched property models.
- Attributes Update: Updating the mathematical attributes of the vertices of the global hologram based on the solutions obtained from the equations.
Enhanced Model Selection
A critical challenge in HGR is efficiently selecting the appropriate graph models to match. To address this, a model selection agent implements deep reinforcement learning to select the graph model at each reasoning step. The objective is to find a deterministic policy that maximizes the expected cumulative rewards.
Experimental Design
Datasets and Evaluation Metrics
The experiments are primarily conducted on Geometry3K, a comprehensive dataset designed for evaluating geometry problem-solving systems. Geometry3K consists of 3,002 SAT-style APGDs. Each problem in the dataset is presented as a single-choice question with four choices, accompanied by problem text, a geometric diagram, and explicit parsing annotations in a formal language.
Evaluation Metrics
To evaluate the performance in solving APGDs, two primary metrics are used:
- Accuracy: Determined by whether the numerical result produced is closest to the correct answer among four choices.
- Reasoning Steps: The average number of geometric theorems applied to generate the solution.
Baselines
HGR is compared against several baseline methods recognized for their effectiveness in solving APGDs, including FiLM, FiLM-BERT, FiLM-BART, Inter-GPS, and GeoDRL.
Implementation Details
For the model construction, a graph model pool containing 13 proving models and 51 property models representing different geometric theorems is prepared. The agent is pre-trained on model selection samples and then trained using DQN to refine its policy and improve its performance.
Results and Analysis
Evaluation
The evaluation of HGR’s accuracy on the Geometry3K dataset demonstrates its superior capabilities in solving APGDs compared to baseline methods. Specifically, HGR achieves an overall accuracy of 68.7%, which improves to 89.6% when using Ground Truth (GT) parsing results. This performance is comparable to the state-of-the-art GeoDRL model and surpasses Inter-GPS, particularly in solving problems related to area calculations or circle type.
Ablation Study
The ablation study evaluated the impact of various components in HGR on Geometry3K. The results demonstrate the significance of each component. The removal of the model selection agent results in a notable decrease in overall accuracy, highlighting the agent’s crucial role in efficiently selecting the appropriate graph models. The removal of proving models and property models also significantly reduces accuracy, highlighting their critical roles in the reasoning process.
Discussion
HGR offers the most comprehensive interpretability compared to other APGD solvers. It not only demonstrates the specific geometric theorems applied to corresponding geometric primitives at each step but also generates equations that demonstrate the algebraic relations between primitives. Additionally, through the use of graph model relation templates, HGR provides human-readable solutions, making it highly suitable for educational applications.
Overall Conclusion
This paper has presented HGR, a high-performance method for solving APGDs. The hologram reasoning scheme played a main role in improving solving accuracy, computing efficiency, and enhancing the interpretability of the solution. The paper’s contributions include the proposal of the hologram, a model-matching method, and a deep reinforcement learning method for model selection.
Future work can focus on improving hologram construction and relation acquisition, transferring hologram reasoning to other types of problems, and integrating methods for solving APGDs and word algebra problems into a uniform method.
Code:
https://github.com/ferretdoll/hgr