Authors:
Milan Papež、Martin Rektoris、Václav Šmídl、Tomáš Pevný
Paper:
https://arxiv.org/abs/2408.09451
Introduction
Graphs are a fundamental framework for representing real or abstract objects and their hierarchical interactions in a diverse range of scientific and engineering applications. These include discovering new materials, developing personalized diagnostic strategies, and estimating time of arrival. However, designing probabilistic models for graphs is challenging due to their highly complex and combinatorial structures. Traditional approaches often struggle to handle this complexity effectively.
Deep generative models, which rely on expressive graph neural networks, have recently made significant progress in capturing complex probability distributions over graphs. However, these models are intractable and unable to answer basic probabilistic inference queries without resorting to approximations. To address this, the authors propose Graph Sum-Product Networks (GraphSPNs), a tractable deep generative model that provides exact and efficient inference over arbitrary parts of graphs. This study investigates different principles to make SPNs permutation invariant and demonstrates that GraphSPNs can generate novel and chemically valid molecular graphs, sometimes outperforming existing intractable models.
Related Work
Sum-Product Networks (SPNs)
Sum-Product Networks (SPNs) are deep generative models for fixed-size tensor data. They are tractable, meaning they can answer a large family of complex probabilistic queries exactly and efficiently under certain assumptions. SPNs contain several layers of computational units, including sum layers, product layers, and input layers. Each layer is defined over its scope, a subset of the input. The key benefit of SPNs is their ability to provide tractable inference over arbitrary subsets of the input.
Permutation Invariance
Permutation invariance is crucial for exchangeable data structures like sets, graphs, partitions, and arrays. It ensures that the probability of an exchangeable data structure remains the same regardless of its configuration. SPNs are only partially permutation invariant, making them sensitive to the ordering of nodes in a graph. This study aims to address this limitation by investigating different techniques to make GraphSPNs permutation invariant.
Research Methodology
Graph Sum-Product Networks (GraphSPNs)
A GraphSPN is a probability distribution over a graph, where the graph is represented by a feature matrix and an adjacency tensor. The GraphSPN is designed as a joint probability distribution of the feature matrix and the adjacency tensor. To deal with the varying size of graphs, the authors use virtual node-padding, which extends the feature matrix by an extra category to express that there is no node at a specific position in the graph.
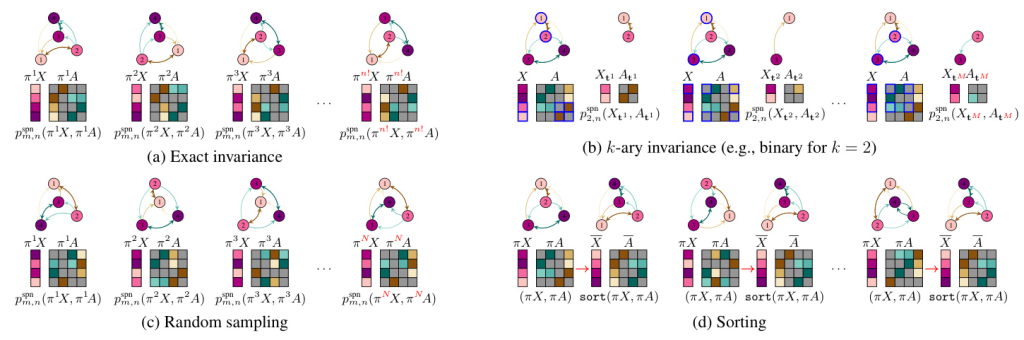
Ensuring Permutation Invariance
The study explores several methods to ensure permutation invariance in GraphSPNs:
-
Exact Permutation Invariance: This method involves averaging over all permutations of the feature matrix and adjacency tensor. However, this approach is computationally costly due to the factorial number of permutations.
-
Sorting: By ensuring that the GraphSPN always sees a user-defined, canonical representation of the graph, permutation invariance is guaranteed. This method involves sorting each instance of the graph before entering the GraphSPN, significantly reducing computational complexity.
-
Approximate Permutation Invariance: This method includes k-ary sub-graphs and random sampling. The k-ary permutation invariance reduces complexity by averaging over all k-node induced sub-graphs, while random sampling approximates permutation invariance by averaging over a subset of random permutations.
Experimental Design
Dataset
The experiments are conducted on the QM9 dataset, a standard benchmark for deep generative models for molecular design. The QM9 dataset contains around 134,000 stable, small organic molecules with at most 9 atoms of 4 different types.
Metrics
The study adopts standard metrics for the molecule generation task:
- Validity (V): The percentage of chemically valid molecules.
- Validity without check (V w/o check): The percentage of chemically valid molecules without any correction mechanisms.
- Uniqueness (U): The percentage of valid and unique molecules.
- Novelty (N): The percentage of valid molecules not in the training data.
GraphSPN Variants
The study considers several GraphSPN variants:
- Sort: Implements sorting for permutation invariance.
- k-ary: Implements k-ary sub-graphs for approximate permutation invariance.
- Rand: Implements random sampling for approximate permutation invariance.
- None: No invariance properties.
Results and Analysis
Unconditional Molecule Generation
The results show that all GraphSPN variants achieve 100% validity due to the posthoc validity correction mechanism. However, the effectiveness of this correction depends on the validity without check. The sort variant delivers the best results, as its validity without check is highest. This is because the sort variant imposes the canonical ordering of atoms in each molecule, simplifying the target data distribution and making it easier for the SPN to be trained successfully.
Conditional Molecule Generation
The study also demonstrates the tractable probabilistic inference capability of GraphSPNs through conditional molecule generation. The results show that the newly generated parts of each molecule vary in size and composition, illustrating the flexibility and effectiveness of GraphSPNs.
Overall Conclusion
This study investigates different ways of ensuring permutation invariance in SPNs and proposes GraphSPNs, a novel class of tractable deep generative models for exact and efficient probabilistic inference over graphs. The results show that GraphSPNs are competitive with existing deep generative models for graphs. Among the proposed GraphSPN variants, the best performance is achieved with the one based on canonical ordering. This demonstrates that canonical ordering simplifies the target data distribution, making it easier for an SPN to be trained successfully.
The study contributes to the field by addressing the challenge of permutation invariance in SPNs and providing a tractable solution for probabilistic inference over graphs. The proposed GraphSPNs have significant potential for applications in molecular design and other domains requiring efficient and accurate graph-based probabilistic models.
Code:
https://github.com/mlnpapez/graphspn