Authors:
Xiner Li、Yulai Zhao、Chenyu Wang、Gabriele Scalia、Gokcen Eraslan、Surag Nair、Tommaso Biancalani、Aviv Regev、Sergey Levine、Masatoshi Uehara
Paper:
https://arxiv.org/abs/2408.08252
Introduction
Diffusion models have emerged as powerful generative models capable of capturing the natural design spaces of various domains, including images, molecules, DNA, RNA, and protein sequences. However, the challenge lies in optimizing downstream reward functions while preserving the naturalness of these design spaces. Existing methods often require differentiable proxy models or computationally expensive fine-tuning of diffusion models. This paper introduces a novel method that addresses these challenges by proposing an iterative sampling method that integrates soft value functions into the standard inference procedure of pre-trained diffusion models.
Related Works
The paper categorizes related works into non-fine-tuning methods and fine-tuning methods for optimizing downstream functions in diffusion models. Non-fine-tuning methods include classifier guidance and Best-of-N, while fine-tuning methods involve classifier-free guidance and RL-based fine-tuning. The paper also discusses discrete diffusion models and decoding in autoregressive models, highlighting the limitations of existing methods and the advantages of the proposed approach.
Preliminaries and Goal
Diffusion Models
Diffusion models aim to learn a sampler given data consisting of pairs (x, c). The training process involves introducing a forward process and learning a backward process to match the induced distributions. The paper provides examples of parameterizations for continuous and discrete spaces, explaining the training process and the goal of generating samples with high rewards while preserving naturalness.
Objective: Generating Samples with High Rewards While Preserving Naturalness
The objective is to sample from a distribution that optimizes reward functions while maintaining the naturalness of the generated samples. The paper formalizes this goal and discusses existing methods, focusing on non-fine-tuning-based approaches.
Soft Value-Based Decoding in Diffusion Models
Key Observation
The paper introduces the concept of soft value functions and soft optimal policies, explaining how they represent the expected future reward from intermediate noisy states. The key observation is that the distribution induced by soft optimal policies matches the target distribution, enabling the development of a new fine-tuning-free optimization algorithm.
Inference-Time Algorithm
The proposed algorithm, SVDD (Soft Value-Based Decoding in Diffusion Models), is an iterative sampling method that integrates soft value functions into the standard inference procedure of pre-trained diffusion models. The algorithm involves generating multiple samples from pre-trained policies and selecting the sample with the highest value function at each time step.
Learning Soft Value Functions
The paper describes two main approaches for learning soft value functions: Monte Carlo regression and posterior mean approximation. Monte Carlo regression involves regressing reward functions onto noisy states, while posterior mean approximation leverages pre-trained diffusion models to estimate value functions without additional training.
Advantages, Limitations, and Extensions of SVDD
Advantages
SVDD offers several advantages, including no fine-tuning, no need for constructing differentiable models, proximity to pre-trained models, and robustness to reward over-optimization. These advantages make SVDD suitable for various scientific domains where non-differentiable reward feedback is common.
Potential Limitations
The approach requires more computational resources or memory during inference time and may be less effective if significant changes to pre-trained models are desired.
Extensions
The paper discusses potential extensions, such as using likelihood/classifier as a reward, combining SVDD with sequential Monte Carlo, and applying SVDD to fine-tuning.
Experiments
Settings
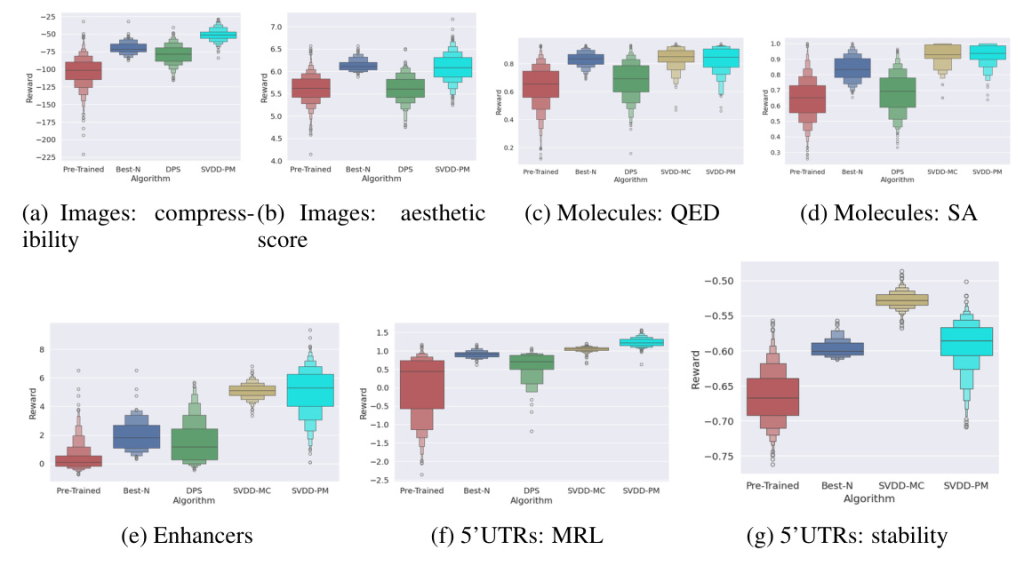
The experiments compare SVDD with baselines, including pre-trained models, Best-of-N, and DPS. The datasets and reward models used in the experiments include images, molecules, DNAs, and RNAs. The paper provides details on the pre-trained diffusion models and downstream reward functions used in the experiments.
Results
The results demonstrate that SVDD outperforms baseline methods in generating high-reward samples. The paper presents histograms of generated samples in terms of reward functions and compares the performance of SVDD with baselines. The superiority of SVDD-MC and SVDD-PM appears to be domain-dependent, with SVDD-PM generally being more robust.
Ablation Studies
The paper conducts ablation studies to assess the performance of SVDD as the number of samples (M) varies. The performance gradually reaches a plateau as M increases, indicating the effectiveness of the proposed approach.
Conclusion
The paper proposes a novel inference-time algorithm, SVDD, for optimizing downstream reward functions in pre-trained diffusion models. SVDD eliminates the need for constructing differentiable proxy models and demonstrates effectiveness across various domains. Future work includes conducting experiments in other domains, such as protein sequence optimization and controllable 3D molecule generation.