Authors:
Majid Ghasemi、Amir Hossein Moosavi、Ibrahim Sorkhoh、Anjali Agrawal、Fadi Alzhouri、Dariush Ebrahimi
Paper:
https://arxiv.org/abs/2408.07712
Introduction
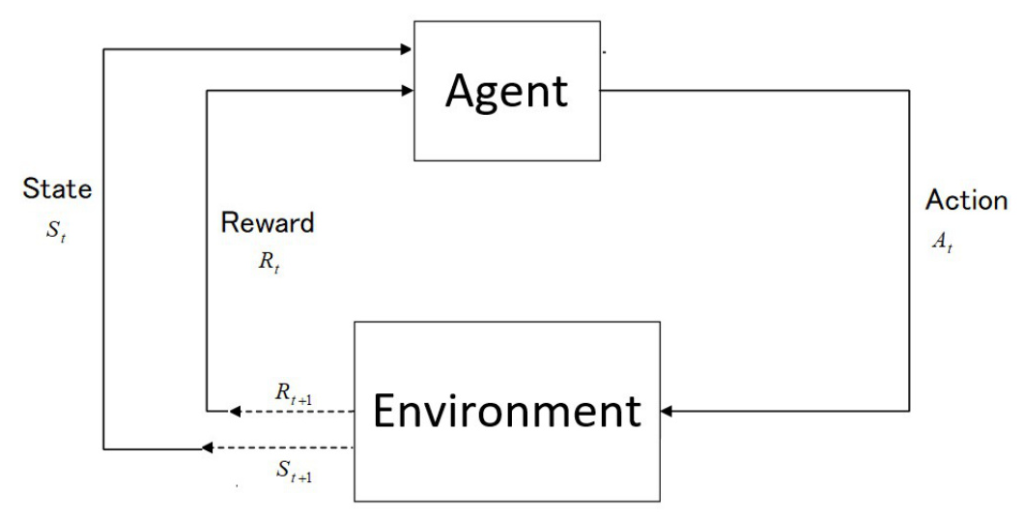
Reinforcement Learning (RL) is a branch of Artificial Intelligence (AI) that focuses on training agents to make decisions by interacting with their environment to maximize cumulative rewards. Unlike supervised learning, where an agent learns from labeled examples, or unsupervised learning, which is based on detecting patterns in the data, RL involves an autonomous agent that must make intuitive decisions and learn from its actions. The key idea is to learn how the world works (e.g., what action gets a reward and which does not) to maximize cumulative rewards over time through trial-and-error exploration.
Key Concepts in RL
- States (s): Represents a specific condition or configuration of the environment at a given time as perceived by the agent.
- Actions (a): The set of possible moves or decisions an agent can make while interacting with the environment.
- Policies (π): Guides the behavior of a learning agent by mapping perceived states of the environment into actions.
- Rewards (r): Provides the agent with an objective at each time step, defining both local and global goals that the agent aims to achieve over time.
Environment Model
An environment model is an approximation or prediction of the environment, mapping out what will be available (the next state and reward) given a particular input from the state and action. RL approaches that use models are called model-based methods, whereas those relying solely on trial-and-error learning are model-free methods.
Example: RL Agent Navigating a Maze
Consider an RL agent navigating a maze. The state represents the agent’s current position within the maze. The actions could be moving north, south, east, or west. The policy dictates which direction the agent should move based on its current state. The reward signal might give a positive reward when the agent reaches the end of the maze and negative rewards for hitting walls or making incorrect moves.
!
Challenges in RL
- Balancing Exploration with Exploitation: The agent must try new actions to gather more information about the environment (exploration) while using its current knowledge to make decisions that maximize immediate rewards (exploitation).
- Formulating Problems with Markov Decision Processes (MDPs): MDPs model decision-making where outcomes are partly determined by chance and partly controlled by the decision-maker.
K-Armed Bandits
K-Armed Bandits is a simple RL form with a single state called bandit problems. It helps in understanding the nature of RL problems by starting with an easy example.
Evaluative Feedback
Evaluative feedback indicates the chosen action is not good, typical in RL tasks, and depends entirely on the actions taken.
!
Immediate Reinforcement Learning (IRL)
In IRL, you are required to select from a number of options (actions) repeatedly. You receive a numerical reward (or punishment) after each choice based on a stationary probability distribution.
Estimating Action Values
To estimate action-values in K-armed bandit problems, we use the following equation, which represents the action value (Q_t(a)) as the average of the rewards received from that action up to time step (t).
[ Q_t(a) = \frac{\text{sum of rewards when the action } a \text{ is taken prior to time step } t}{\text{number of times the action } a \text{ is taken prior to time step } t} ]
Finite Markov Decision Process
Finite Markov Decision Processes (MDPs) provide a framework for sequential decision-making in which actions affect immediate rewards as well as future outcomes.
State-Transition Probability Function
The state-transition probability function (p(s’, r | s, a)) is defined as follows:
[ p(s’, r | s, a) \equiv Pr{S_t = s’, R_t = r | S_{t-1} = s, A_{t-1} = a} ]
Return
The return, denoted (G_t), is the cumulative sum of rewards received from time step (t) onwards.
For episodic tasks:
[ G_t \equiv R_{t+1} + R_{t+2} + \ldots + R_T ]
For continuing tasks:
[ G_t \equiv R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} ]
Policies and Value Functions: Zero to Hero
Value functions estimate the expected return of the agent being in a certain state (or performing an action in a particular state).
State Value Functions
The state value function (v_{\pi}(s)) represents the expected return starting from state (s) and following policy (\pi).
[ v_{\pi}(s) \equiv E_{\pi} \left[ \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \mid S_t = s \right] ]
Action Value Functions
The action value function (q_{\pi}(s, a)) represents the expected return starting from state (s), taking action (a), and then following policy (\pi).
[ q_{\pi}(s, a) \equiv E_{\pi} \left[ G_t \mid S_t = s, A_t = a \right] ]
Bellman Equation
The Bellman equation for (v_{\pi}) is:
[ v_{\pi}(s) \equiv E_{\pi}[G_t \mid S_t = s] = E_{\pi}[R_{t+1} + \gamma G_{t+1} \mid S_t = s] ]
Optimal Policies and Optimal Value Functions
An optimal policy (\pi^) is better than or equal to all other policies, sharing the same optimal state-value function (v^).
Optimal State Value Function
[ v^*(s) \equiv \max_{\pi} v_{\pi}(s) ]
Optimal Action Value Function
[ q^*(s, a) \equiv \max_{\pi} q_{\pi}(s, a) ]
Bellman Optimality Equations
The Bellman optimality equations for the optimal state value function (v^(s)) and the optimal action value function (q^(s, a)) are:
[ v^(s) = \max_a E[R_{t+1} + \gamma v^(S_{t+1}) \mid S_t = s, A_t = a] ]
[ q^(s, a) = E[R_{t+1} + \gamma \max_{a’} q^(S_{t+1}, a’) \mid S_t = s, A_t = a] ]
Policy Evaluation (Prediction)
Policy evaluation involves computing the state-value function (v_{\pi}) for a given policy (\pi).
[ v_{\pi}(s) \equiv E_{\pi}[R_{t+1} + \gamma G_{t+1} \mid S_t = s] ]
Policy Improvement
To determine if a policy can be improved, we compare the value of taking a different action (a) in state (s) with the current policy.
[ q_{\pi}(s, a) \equiv E[R_{t+1} + \gamma v_{\pi}(S_{t+1}) \mid S_t = s, A_t = a] ]
Policy Improvement Theorem
The policy improvement theorem states that if (q_{\pi}(s, \pi'(s)) \geq v_{\pi}(s)) for all states (s), then the new policy (\pi’) is at least as good as the original policy (\pi).
Policy Iteration
Policy iteration involves alternating between policy evaluation and policy improvement to obtain a sequence of improving policies and value functions.
[ \pi_0 \rightarrow v_{\pi_0} \rightarrow \pi_1 \rightarrow v_{\pi_1} \rightarrow \pi_2 \rightarrow \ldots \rightarrow \pi^ \rightarrow v^ ]
Value Iteration
Value iteration combines policy improvement with a truncated form of policy evaluation. The update rule for value iteration is:
[ v_{k+1}(s) \equiv \max_a E[R_{t+1} + \gamma v_k(S_{t+1}) \mid S_t = s, A_t = a] ]
Terminology
Understanding the various methodologies and concepts within RL is essential for the effective design and implementation of RL algorithms.
Model-Free Methods
Model-free methods determine the optimal policy or value function directly without constructing a model of the environment.
Model-Based Methods
Model-based methods predict the outcomes of actions using models, facilitating strategic planning and decision-making.
Off-Policy and On-Policy Methods
- On-Policy Methods: Evaluate and improve the policy used to make decisions.
- Off-Policy Methods: Learn the value of the optimal policy independently of the agent’s actions.
A Timeline of Reinforcement Learning Evolution
Early Foundations (1950s-1960s)
- 1954: Marvin Minsky’s SNARC, an early neural network-based machine.
- 1954: Richard Bellman’s work on dynamic programming.
Theoretical Development (1970s-1980s)
- 1972: Klopf’s work on drive-reduction theory in neural networks.
- 1984: Barto, Sutton, and Anderson developed the concept of temporal difference (TD) learning.
- 1989: Watkins introduced Q-learning.
Early Applications and Further Theory (1990s)
- 1992: Watkins and Dayan formalized Q-learning.
- 1994: Rummery and Niranjan developed SARSA.
- 1996: Chris Watkins’ Dyna-Q algorithm.
Advances in Algorithms and Applications (1999-2000s)
- 1999: Konda and Tsitsiklis introduced actor-critic methods.
- 1999: Ng, Harada, and Russell’s work on apprenticeship learning.
- 2001: Tsitsiklis and Van Roy developed the theory of least-squares temporal difference (LSTD) learning.
Deep Reinforcement Learning and Breakthroughs (2010s)
- 2013: Mnih et al. introduced Deep Q-Networks (DQN).
- 2016: Silver et al. developed AlphaGo.
- 2017: Schulman et al. proposed Proximal Policy Optimization (PPO).
- 2018: Hessel et al. presented Rainbow.
Current Trends and Future Directions
Recent trends focus on interpretability, hierarchical RL, multi-agent RL, integrations with transformers and large language models (LLMs), human-in-the-loop RL, social reinforcement learning, transfer learning, lifelong learning, and continual learning.
Essential Algorithms: An Overview
TD Learning
Temporal Difference (TD) Learning updates are made based on the difference between predicted and actual rewards.
[ V(s) \leftarrow V(s) + \alpha [R_{t+1} + \gamma V(S_{t+1}) – V(s)] ]
Q-Learning
Q-Learning is an off-policy algorithm that learns the value of an optimal policy independently of the agent’s actions.
[ Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma \max_{a’} Q(s’, a’) – Q(s, a)] ]
State-Action-Reward-State-Action (SARSA)
SARSA is an on-policy algorithm where the policy is updated based on the action taken by the current policy.
[ Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma Q(s’, a’) – Q(s, a)] ]
REINFORCE
REINFORCE is an on-policy algorithm that uses Monte Carlo methods to update the policy.
[ \theta \leftarrow \theta + \alpha \nabla_{\theta} \log \pi_{\theta}(a|s) G_t ]
Actor-Critic
Actor-Critic methods combine value function (critic) and policy (actor) updates.
[ \delta_t = R_{t+1} + \gamma V(S_{t+1}) – V(S_t) ]
[ \theta \leftarrow \theta + \alpha \delta_t \nabla_{\theta} \log \pi_{\theta}(A_t|S_t) ]
Soft Actor-Critic
Soft Actor-Critic (SAC) maximizes both expected reward and entropy.
[ L(\theta) = E_{(s,a) \sim D} [-Q(s, a) + \alpha \log \pi_{\theta}(a|s)] ]
Dyna-Q
Dyna-Q combines model-free and model-based methods by integrating planning, acting, and learning.
[ Q(s, a) \leftarrow Q(s, a) + \alpha [r + \gamma \max_{a’} Q(s’, a’) – Q(s, a)] ]
Deep Q-Network
Deep Q-Network (DQN) combines Q-learning with deep neural networks to handle high-dimensional state spaces.
[ Q(s, a; \theta) \leftarrow Q(s, a; \theta) + \alpha [r + \gamma \max_{a’} Q(s’, a’; \theta’) – Q(s, a; \theta)] ]
Trust Region Policy Optimization
Trust Region Policy Optimization (TRPO) ensures large updates do not destroy the learned policy by enforcing a trust region.
[ \max_{\theta} E_{s \sim \rho_{\pi}, a \sim \pi_{\theta}} \left[ \frac{\pi_{\theta}(a|s)}{\pi_{\theta_{\text{old}}}(a|s)} A_{\pi_{\theta_{\text{old}}}}(s, a) \right] ]
Proximal Policy Optimization
Proximal Policy Optimization (PPO) improves on TRPO by simplifying the algorithm while retaining its performance.
[ L_{\text{CLIP}}(\theta) = E_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 – \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] ]
Resources to Learn Reinforcement Learning
Books
- “Reinforcement Learning: An Introduction” by Richard S. Sutton and Andrew G. Barto
- “Deep Reinforcement Learning Hands-On” by Maxim Lapan
- “Grokking Deep Reinforcement Learning” by Miguel Morales
- “Algorithms for Reinforcement Learning” by Csaba Szepesvári
Online Courses
- Coursera: Reinforcement Learning Specialization by University of Alberta
- Udacity: Deep Reinforcement Learning Nanodegree
- edX: Fundamentals of Reinforcement Learning by University of Alberta
- Reinforcement Learning Winter 2019 (Stanford)
Video Lectures
- DeepMind x UCL — Reinforcement Learning Lectures Series
- David Silver’s Reinforcement Learning Course
- Pascal Poupart’s Reinforcement Learning Course – CS885
- Sarath Chandar’s Reinforcement Learning Course
Tutorials and Articles
- OpenAI Spinning Up in Deep RL
- Deep Reinforcement Learning Course by PyTorch
- RL Adventure by Denny Britz
Online Communities and Forums
- Reddit: r/reinforcementlearning
- Stack Overflow
- AI Alignment Forum
Conclusion
This paper has introduced the fundamental concepts and methodologies of Reinforcement Learning (RL) in an accessible manner for beginners. By providing a detailed description of the core elements of RL, such as states, actions, policies, and reward signals, we have established a foundation for understanding how RL agents learn and make decisions. The purpose of this paper is to provide an overview of various RL algorithms, including both model-free and model-based approaches, in order to illustrate the diversity of approaches within the field of RL. To facilitate deeper learning and practical application of RL, this guide aims to provide new learners with the necessary knowledge and confidence to embark on their RL journey.
!
!