Authors:
Samuel Chevalier、Duncan Starkenburg、Krishnamurthy、Dvijotham
Paper:
https://arxiv.org/abs/2408.10491
Introduction
Background
Formal verification is a critical process in ensuring the reliability and robustness of systems, particularly those involving Neural Networks (NNs). This process involves reformulating NNs into mathematical programs optimized for verification. However, the non-convex nature of these reformulations poses significant challenges, necessitating the use of convex relaxations for nonlinear activation functions.
Problem Statement
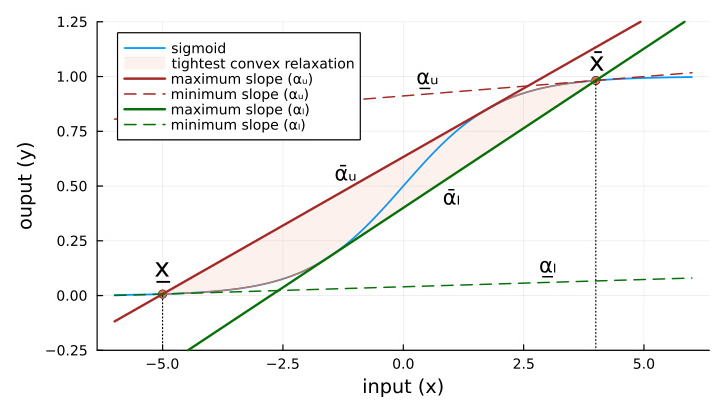
Common relaxations, such as static linear cuts for “S-shaped” activation functions like the sigmoid, often result in overly loose bounds, which can slow down the verification process. This paper introduces a novel approach to derive tunable hyperplanes that tightly bound the sigmoid activation function, thereby improving the efficiency and accuracy of formal verification.
Related Work
Existing Approaches
Several methods have been developed to address the challenges of verifying NNs with nonlinear activation functions:
- α-CROWN: Utilizes optimizable linear relaxations to achieve tight lower bounds on verification problems.
- Multi-Neuron Guided Branch-and-Bound: Employs branching points to choose linear cuts that statically bound portions of activation functions.
- GenBaB: A general framework for performing Branch-and-Bound over various nonlinear activations, including sigmoid, tanh, sine, GeLU, and bilinear functions.
Limitations
Despite these advancements, existing methods struggle to tightly approximate S-shaped activations like the sigmoid function. This paper aims to address this gap by proposing a maximally tight linear relaxation strategy for sigmoid activation functions.
Research Methodology
Deriving Tight Bounds
The core contribution of this paper is the derivation of an explicit mapping between the linear slope and y-intercept of a tangent line that tightly bounds a sigmoid function. This mapping is differentiable and tunable, allowing for the tightest possible element-wise convex relaxation of the sigmoid function.
Backward NN Evaluation
A backward NN evaluation routine is proposed to dynamically detect whether a sigmoid should be upper or lower bounded at each step of a gradient-based solve. This ensures that the tightest bounds are applied throughout the verification process.
Sequential Quadratic Programming
To ensure feasible projection in the dual space, a sequential quadratic program is designed to efficiently precompute the maximum slope bounds of all tunable slopes.
Experimental Design
Planning and Designing the Experiment
The experiments were designed to test the effectiveness of the proposed α-sig method against existing state-of-the-art methods like α-CROWN. The experiments involved optimizing over a range of randomly generated sigmoid-based NNs with varying sizes and weight distributions.
Data Preparation
NNs with four dense layers and sigmoid activation functions were generated, followed by a dense linear layer. The verification problem aimed to minimize the sum of all outputs, with an allowable infinity norm perturbation of ∥x∥∞ ≤ 1.
Conditions
Two sets of experiments were conducted:
1. Varying Weight Distributions: NNs were initialized with progressively shrinking weight parameter variances.
2. Consistent Weight Distributions: NNs were initialized with consistent weight and bias distributions.
Results and Analysis
Experiment 1: Varying Weight Distributions
The results showed that α-sig provided marginally tighter bounds than α-CROWN in most cases. However, as NN models shrank in size and weight parameter variances dropped, α-CROWN’s advantage in primal bound solving became more apparent.
Experiment 2: Consistent Weight Distributions
In this experiment, α-sig consistently outperformed α-CROWN, demonstrating its effectiveness in providing tighter bounds, especially when weight parameter variances were larger.
Computational Efficiency
α-sig demonstrated substantial improvements in computational efficiency, being up to two orders of magnitude faster than α-CROWN in some cases.
Overall Conclusion
Summary
This paper presents a novel approach to achieve the tightest relaxation of sigmoid activation functions for formal verification. By deriving tunable hyperplanes and employing a backward NN evaluation routine, the proposed α-sig method provides a maximally tight convex relaxation of the sigmoid function.
Future Work
Future research will focus on integrating α-sig with other verification frameworks like LiRPA/CROWN to further enhance activation function bounding. Additionally, the approach will be extended to other S-shaped activation functions and the multi-variate softmax function.
Final Thoughts
The proposed α-sig method represents a significant advancement in the formal verification of NNs, offering both improved bound tightness and computational efficiency. This work lays the foundation for more robust and scalable verification technologies in the future.