Authors:
Elisa Böhl、Stefan Ellmauthaler、Sarah Alice Gaggl
Paper:
https://arxiv.org/abs/2408.08150
Introduction
Answer Set Programming (ASP) is a declarative programming paradigm that has gained traction in both theoretical and practical applications. ASP is particularly useful for solving complex problems such as planning and configuration. This paper explores different techniques to reuse logic program parts (multi-shot) by solving the arcade game Snake. The game is interesting because winning can be assured by solving the NP-hard problem of Hamiltonian Cycles. The paper demonstrates five implementations in clingo and compares their performance.
Preliminaries
Answer Set Programming
ASP is based on stable model semantics and involves defining a set of rules. A rule in ASP is of the form:
a1; ... ; am :- am+1, ..., an, not an+1, ..., not ao.
where each atom ai is a predicate symbol with terms built using constants and variables. ASP programs can include conditional literals, cardinality constraints, and optimization statements to ease programming.
Multi-Shot ASP in clingo
clingo provides an API to access ASP functionality within an imperative language like Python. This allows for altering and repeatedly running logic programs. Key features include assumptions, externals, and nogoods, which influence the solving process.
Graphs, Paths, and Hamiltonian Cycles
A grid graph G(n, m) is an undirected graph formed by a rectangular grid of vertices. A Hamiltonian Cycle (HC) in a grid graph is a path that passes through every vertex without repetition. Only grid graphs with an even number of vertices admit an HC.
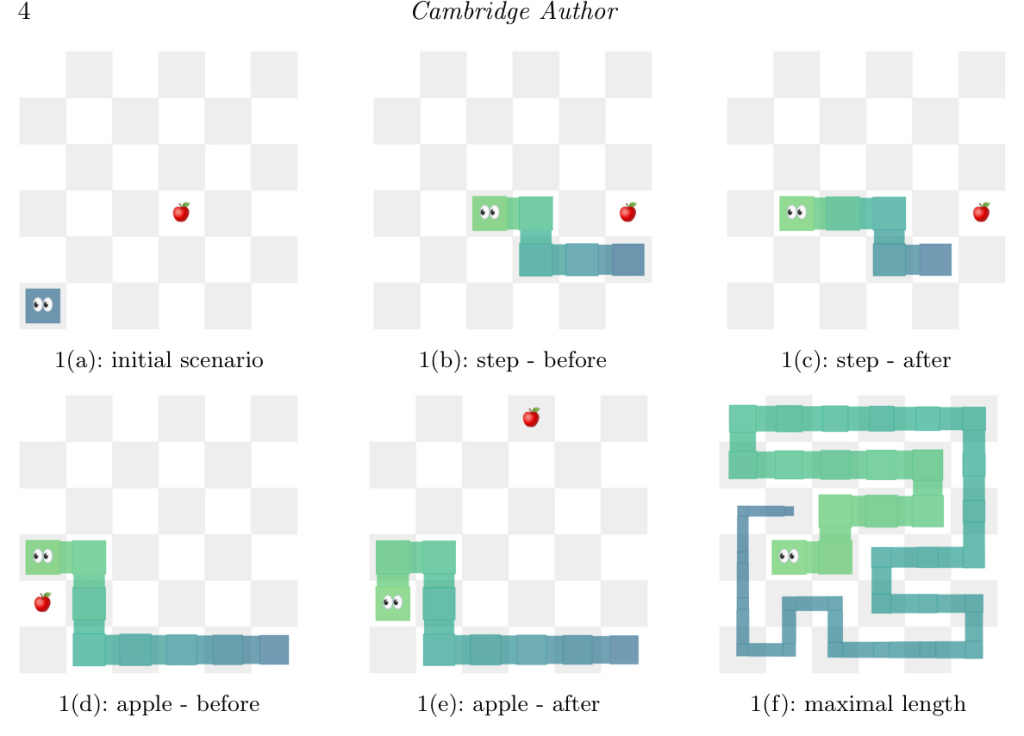
Snake Game
The Snake game involves steering a snake’s head on a grid to consume apples and grow in length. The game starts with a snake of length one and one apple on a random field. The game is won when the snake reaches its maximal length, filling the entire grid.
Formalizing and Winning Snake Optimally with ASP
Goal Specification
The objectives are:
1. Guarantee winning the game by ensuring the snake can always reach maximal length (G1).
2. Minimize the number of snake movements (G2).
3. Minimize computation time (G3).
Problem Description for Iterations
The problem can be formalized for one iteration of the Snake game. The general problem involves finding a path from the snake to the apple on a grid graph. To ensure future iterations are solvable, Hamiltonian Cycles are used.
Snake Strategies
Two strategies are introduced:
1. Naive Strategy: Derives an HC in the first iteration and follows it repeatedly.
2. Conservative Strategy: Allows the HC to change between iterations, solving Minimal Hamiltonian Snake (MHS) problems.
Multi-Shot Implementation Approaches
Five different clingo implementations are proposed to solve the Snake game:
One-Shot
This approach grounds and solves the logic program for each iteration from scratch. It is simple and easy to debug but may be inefficient for iterative problems.
Ad Hoc
This approach adds and removes rules using external atoms as guards. It is flexible but may require a deeper understanding of the logic program’s dependencies.
Preground
All required temporary rules are pregrounded with externals to switch them on and off. This approach is efficient for compact programs with many iterations but lacks the flexibility to add rules on the fly.
Assume
Assumptions are used to fix truth values for non-external atoms. This approach is flexible but may lead to less organized code.
Nogood
Nogoods influence the search progress by adding custom constraints during the solve call. This approach combines the expressivity of preground with the flexibility of assumptions but requires sophisticated knowledge of the clingo API.
Experimental Evaluation
Setup
The performance of the five approaches was compared by solving 100 Snake games for different grid sizes. The experiments were run on a MacBook Pro with clingo and Python. The evaluation focused on win/lose ratio, total number of steps, and total computation time.
Evaluation
The results showed that all approaches guaranteed winning the game. One-shot performed well for smaller grids but struggled with larger grids due to the grounding bottleneck. Multi-shot approaches utilized past search progress, reducing the impact of timeouts and outperforming one-shot for larger grids.
Conclusion and Future Work
The paper demonstrated that multi-shot implementations can substantially benefit applications with limited resources. While one-shot is straightforward to implement, multi-shot approaches can utilize previous solving history to improve performance. Future work may involve exploring other showcase applications and refining problem descriptions to derive even shorter paths while guaranteeing a win.
The illustrations provided in the paper help visualize the Snake game scenarios and the performance of different approaches. The experimental results highlight the advantages and trade-offs of each implementation strategy.