Authors:
Paper:
https://arxiv.org/abs/2408.10709
Introduction
Dynamic systems are ubiquitous in our world, and understanding them is crucial for predicting and controlling their outcomes. The Learning from Interpretation Transition (LFIT) framework is a powerful tool for automatically constructing models of dynamic systems in the form of logic programs based on observed state transitions. Traditional symbolic algorithms implementing LFIT are interpretable and verifiable but struggle with noisy data and unobserved transitions. Neural networks, on the other hand, can handle noise and generalize better but often suffer from overfitting and lack interpretability.
In this paper, the authors introduce δLFIT2, a novel approach that leverages variable permutation invariance inherent in symbolic domains. This technique ensures that the permutation and naming of variables do not affect the results, enhancing the scalability and effectiveness of the method.
Related Work
Extraction-based Methods
CIL2-P and NN-LFIT are foundational methods for extracting symbolic knowledge from neural networks. These methods, however, impose heavy constraints on the neural network architecture, limiting their applicability.
Differentiable Programming-based Methods
Methods like the Apperception Engine, δILP, and Logic Tensor Network use gradient descent to learn matrices that can be transformed into symbolic knowledge. These methods face scalability issues as the size of the learnable matrix grows with the problem size.
Integration-based Methods
NeurASP and Deepstochlog integrate symbolic reasoning engines with neural network models. Recent works combining large language models (LLMs) and reasoning also fall into this category but still struggle with understanding and verifying neural network outputs.
Invariance in Deep Learning
Recent research has focused on exploiting permutation invariance in problem domains to improve performance. This work extends the focus to invariance within the semantics of the problem.
Research Methodology
Normal Logic Program for State Transitions
A normal logic program (NLP) for state transitions consists of rules that describe how the state of a variable at time ( t+1 ) depends on the states of other variables at time ( t ). The LFIT framework uses these rules to simulate state transitions in dynamic systems.
LFIT Framework
The LFIT framework takes a set of state transitions and an initial NLP to output a logic program consistent with the input transitions. Symbolic algorithms implementing LFIT struggle with noisy or missing data, prompting the need for neural-symbolic AI methods.
δLFIT+
δLFIT+ is a neural network implementation of the LFIT framework that directly outputs symbolic knowledge. It uses Set Transformer to process state transitions in a permutation-invariant manner but faces challenges with variable permutation within states and a complex loss function.
Experimental Design
Variable Assignment Invariance
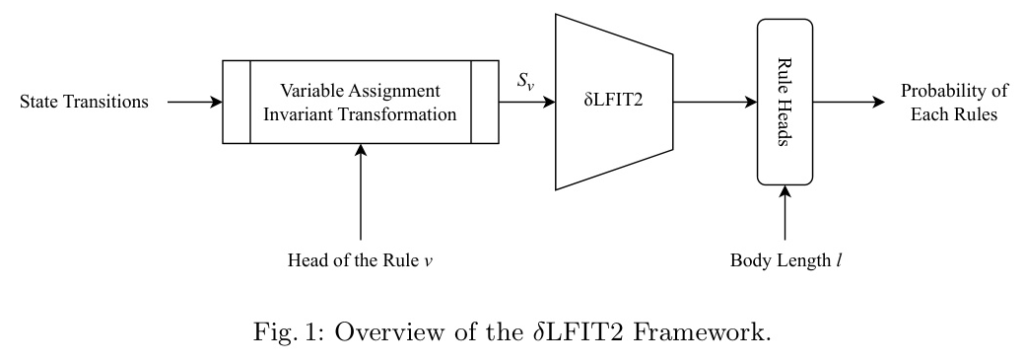
δLFIT2 introduces a variable assignment invariant technique to address the issue of variable permutation within states. By abstracting variable names and reordering variables consistently, the learning problem for the neural network is simplified.
Dynamic Rule Heads
δLFIT2 constructs separate output layers for each body length of rules, dynamically loading them into memory when required. This approach addresses the scalability issue and ensures a smoother loss function.
Overview of δLFIT2
The δLFIT2 framework processes state transitions through a variable assignment invariant transformation, followed by a neural network model that outputs the probability of each rule. The model architecture includes an embedding layer, Set Transformer, and feed-forward layers.
Results and Analysis
Datasets and Experimental Methods
The experiments use boolean networks from the PyBoolNet repository, converted into logic programs. The Mean Squared Error (MSE) metric evaluates the difference between state transitions generated by the original and predicted programs.
Experimental Results
δLFIT2 outperforms NN-LFIT, δLFIT, and δLFIT+ in most cases, particularly in handling noisy data and avoiding overfitting. The method scales well to larger systems and produces more succinct and minimal rules.
Partial State Transitions
δLFIT2 also performs well when only partial state transitions are provided, recovering rules better than other methods once more than 50% of transitions are given.
Overall Conclusion
The paper introduces δLFIT2, a method that leverages variable assignment invariance to improve the scalability and effectiveness of learning logic programs from state transitions. The proposed method addresses the limitations of δLFIT+ and demonstrates superior performance in handling noisy data, avoiding overfitting, and scaling to larger systems. Future work could extend δLFIT2 to asynchronous semantics and dynamic systems with delay or memory, as well as explore its application to first-order logic.
Acknowledgements
This work was supported by JSPS KAKENHI Grant Number JP22K21302, JP21H04905, the JST CREST Grant Number JPMJCR22D3, and ROIS NII Open Collaborative Research 2024-24S1203.
Implementation Details
The model was implemented in PyTorch 2.1 with Python 3.10, including components like the Set Transformer encoder and decoder, and a feed-forward layer. Specific hyperparameters and training details are provided for δLFIT23 and δLFIT24 models.
Algorithm for Applying to Larger Systems
An algorithm is provided for applying δLFIT2 to larger systems by mapping subsets of variables to indices and using the trained model to obtain rules, which are then mapped back to the original variables.
By leveraging variable assignment invariance and improving the neural network architecture, δLFIT2 represents a significant advancement in learning logic programs from dynamic systems. The method’s ability to handle noisy data, avoid overfitting, and scale to larger systems makes it a promising tool for future research in neural-symbolic AI.