Authors:
Paper:
https://arxiv.org/abs/2408.06797
Stunned by Sleeping Beauty: How Prince Probability Updates His Forecast Upon Their Fateful Encounter
Introduction
The Sleeping Beauty problem is a well-known puzzle in probability theory that has sparked extensive debate since its introduction by Elga in 2000. The problem involves Sleeping Beauty being put to sleep, followed by a coin toss. If the coin lands on Tails, she is woken up on Monday, put back to sleep with her memory erased, and then woken up again on Tuesday. If the coin lands on Heads, she is woken up only on Monday. Each time she wakes up, she is asked to estimate the probability that the coin landed on Heads. This paper argues, using Bayesian probability theory, that the correct answer is 1/3, not 1/2. The argument is strengthened by introducing an additional observer, Prince Probability, who updates his beliefs upon encountering Sleeping Beauty.
A Thirder’s Tale of Beauty and the Prince
Beauty Knowing She is Awake is Nontrivial Information
When Sleeping Beauty wakes up, the fact that she is awake is nontrivial information. If the coin lands on Heads, she is awake for only one hour out of 48 hours. If it lands on Tails, she is awake for two hours out of 48 hours. Using Bayesian probability, the credence she assigns to Heads while being awake is calculated as follows:
[ p(H|SB \text{ awake}) = \frac{p(H) \cdot p(SB \text{ awake}|H)}{p(SB \text{ awake})} = \frac{\frac{1}{2} \cdot \frac{1}{48}}{\frac{1}{2} \cdot \frac{3}{48}} = \frac{1}{3} ]
Thus, Sleeping Beauty should assign a 1/3 probability to Heads when she is awake.
Perspective of Outsider Prince Probability
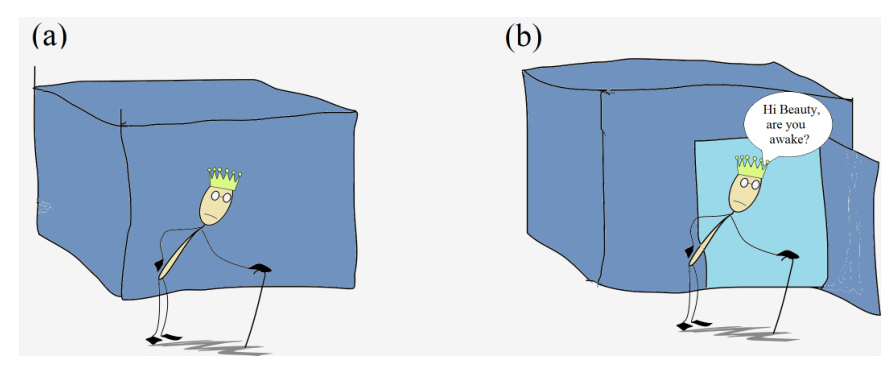
Prince Probability, an outsider who may or may not meet Sleeping Beauty, initially assigns a 1/2 probability to Heads. Upon meeting an awake Sleeping Beauty, he updates his credence to 1/3 for Heads, as she is more likely to be awake under Tails. This scenario is illustrated in Figure 1.
What if Sleeping Beauty Knew She Was Dreaming?
If Sleeping Beauty knows she is dreaming (and thus asleep), she would increase her credence in Heads. The probability calculations show that her credence in Heads while dreaming depends on the time she is awake each time she is woken up. For example, if she is awake for 23 hours, she assigns a credence of approximately 0.926 to Heads while dreaming.
Variations of the Sleeping Beauty Problem
The Copy Sleeping Beauty Version
In this variation, there are two identical labs. If the coin lands on Tails, a copy of Sleeping Beauty is made and placed in the second lab. Prince Probability, who does not know the outcome of the coin toss, initially assigns a 1/2 probability to Heads. Upon meeting a Sleeping Beauty, he updates his credence to 1/3 for Heads. This scenario supports the argument that Sleeping Beauty should always assign a 1/3 probability to Heads when she wakes up.
Sleeping Beauty and an Unfair Coin Toss
If the coin toss is unfair, with a probability of 1/4 for Heads and 3/4 for Tails, the same Bayesian calculations apply. Prince Probability, upon finding an awake Sleeping Beauty, assigns a 1/7 probability to Heads. This result aligns with the original argument for a fair coin toss.
Relation to Literature on Sleeping Beauty
Elga’s Argument for 1/3 and the Principle of Indifference
Elga’s argument uses the Principle of Indifference for self-locating belief to conclude that Sleeping Beauty should assign a 1/3 probability to Heads when she wakes up. This principle states that similar centered worlds deserve equal credence. Elga’s resolution aligns with the Bayesian argument presented in this paper.
The Thirders vs. the Halfers
The debate between Thirders and Halfers centers on whether Sleeping Beauty gains new information upon waking up. This paper supports the Thirder position by demonstrating that being awake is nontrivial information. The introduction of Prince Probability further strengthens this argument.
The Sleeping Beauty Problem and the Frauchiger–Renner Paradox
The Frauchiger–Renner paradox suggests an inconsistency in using quantum theory to describe itself. The extension of the Sleeping Beauty problem with Prince Probability provides an argument against the Consistency assumption used in the paradox. However, it does not resolve the stronger GHZ–FR paradox, which requires a more radical resolution.
Discussion and Conclusion
This paper argues that 1/3 is the correct answer for Sleeping Beauty when she wakes up and is asked for her credence in Heads. The introduction of Prince Probability, who updates his beliefs upon meeting Sleeping Beauty, supports this conclusion. The paper also discusses variations of the problem and relates the findings to existing literature.
Acknowledgements
The author thanks Caroline Jones for bringing this problem to attention and for many enlightening discussions. Additional thanks to Will Oliver, Rui Soares Barbosa, and Khadija Sarr for their contributions and support.
This blog post provides a detailed interpretation of the academic paper, explaining each section and the key arguments presented. The illustrations from the paper are referenced to enhance understanding.