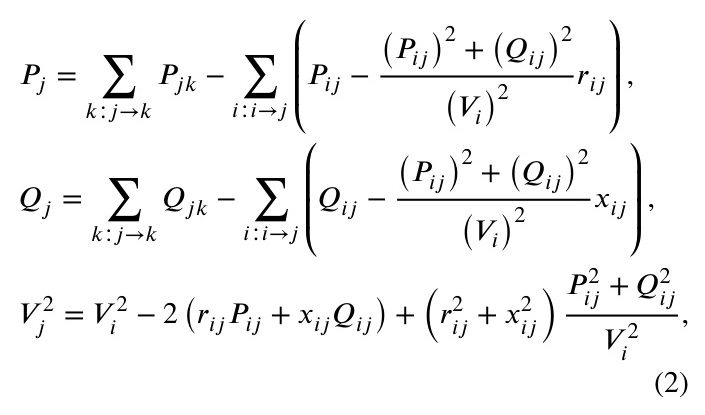Authors:
Paper:
https://arxiv.org/abs/2408.06776
Introduction
As the world moves towards a carbon-neutral society, active distribution networks (ADNs) are increasingly incorporating renewable distributed generators (DGs) such as photovoltaic (PV) systems and wind turbines. These DGs, while beneficial, introduce volatility and uncertainty in power generation, leading to challenges like voltage violations and increased power loss. Inverter-based devices, capable of fast reactive control, present an opportunity for real-time volt-var control (VVC) to optimize voltage profiles and minimize power loss in ADNs. This paper addresses the challenges of limited measurement deployment in ADNs using a robust deep reinforcement learning (DRL) approach.
Preliminary
Inverter-based Volt-Var Control
ADNs with inverter-based devices can be represented as a graph with buses and branches. The objective of inverter-based VVC (IB-VVC) is to minimize active power loss and optimize voltage profiles by controlling the reactive power output of DGs and static Var compensators (SVCs). The optimization problem involves minimizing the active power loss while adhering to voltage and reactive power constraints.
Deep Reinforcement Learning
The goal of reinforcement learning (RL) is to learn a policy that maximizes the expected discounted accumulated reward from a sequence of Markov decision process (MDP) data. In the context of IB-VVC, the state-action value functions are used to evaluate the policy, and the objective is to find a policy that maximizes the state-action value function.
Quantile Regression
Quantile regression is a statistical technique that predicts multiple conditional quantiles of a response variable distribution, providing a comprehensive view of uncertainty and variability in predictions. This technique is used to estimate the conservative state-action value function in the proposed DRL approach.
Problem Formulation: Partially Observable Markov Decision Process
The IB-VVC problem with limited measurement deployment is formulated as a partially observable Markov decision process (POMDP). The state, observation, action, and reward are defined as follows:
State
The state reflects the complete working condition of the ADN, including uncontrollable, controllable, and dependent variables.
Observation
The observation is the partially observable state, which includes only the measurable variables.
Action
The action is related to the controllable variables, defined as the reactive power outputs of DGs and SVCs.
Reward
The reward evaluates the optimization performance of the action, consisting of power loss and voltage violation rewards.
Surrogate Reward
For unknown rewards, surrogate rewards are designed based on measurable variables. The surrogate reward for power loss is the change in active power injection of the root node, and the surrogate reward for voltage violation is based on the measurable bus voltages.
Robust Deep Reinforcement Learning Method
The proposed robust DRL approach addresses the problems of partially observable states and unknown rewards using a conservative critic and surrogate rewards.
Conservative Critic
The conservative critic estimates the uncertainties of state-action values with respect to the partially observable state using quantile regression. This helps in training a robust policy.
Practical Algorithm: Robust Soft Actor-Two-Critic
The robust soft actor-two-critic algorithm combines the soft actor-critic (SAC) framework with the conservative critic and surrogate rewards. The algorithm optimizes the power loss of the whole network and the voltage profile of measurable buses while indirectly improving the voltage profile of other buses.
Minimum Measurement Condition
The proposed robust DRL approach is applicable to different measurement conditions. The minimal measurement condition includes the active power injection of the root bus and a few bus voltage magnitudes.
Simulation
Numerical simulations were conducted on 33, 69, and 118-bus distribution networks to demonstrate the effectiveness of the proposed robust DRL approach.
Effectiveness of the Proposed Robust DRL
The proposed robust DRL approach was tested under three limited measurement conditions and compared with the standard DRL approach under ideal measurement conditions and a model-based optimization approach. The results showed that the robust DRL approach achieved performance close to the standard DRL approach, even under minimal measurement conditions.
The Effect of Partially Observable State and Surrogate Reward
The impact of partially observable states and surrogate rewards was tested under different measurement conditions. The results indicated that the partially observable state degraded the VVC performance slightly, but the surrogate rewards effectively optimized the power loss and voltage violation.
The Effect of Conservative Critic
The effectiveness of the conservative critic was demonstrated by comparing the proposed robust DRL with and without the conservative critic under limited measurement conditions. The conservative critic significantly reduced the voltage violation while slightly increasing the power loss.
Conclusion
This paper proposes a robust DRL approach for IB-VVC in ADNs with limited measurement deployments. The approach addresses the problems of partially observable states and unknown rewards using a conservative critic and surrogate rewards. The simulation results demonstrate the effectiveness of the proposed approach under different measurement conditions.
Illustrations
Figure 1: The overview of the proposed robust deep reinforcement learning approach.
Figure 2: The framework of robust deep reinforcement learning.
Figure 3: The testing results of the proposed robust DRL with partially observable state and surrogate reward (PS) under three measurement conditions, the standard DRL with complete state and complete reward (CC), and the model-based optimization (MB).
Figure 4: The VVC performance of without control and the robust DRL robust approach.
Figure 5: The optimization error in the final 20 episodes.
Figure 6: The optimization error DRL with and without the conservative critic in the final 20 episodes.
References
- Liu, Q., Guo, Y., & Xu, T. (2024). Robust Deep Reinforcement Learning for Inverter-based Volt-Var Control in Partially Observable Distribution Networks. Elsevier.
- Matpower. (n.d.). Retrieved from https://matpower.org
- Pandapower. (n.d.). Retrieved from https://pandapower.org
Note: The illustrations are placeholders and should be replaced with actual images from the paper.