Authors:
Paper:
https://arxiv.org/abs/2408.07945
Introduction
The Rubik’s Cube, a 3 × 3 × 3 single-player combination puzzle, has garnered significant interest within the reinforcement learning community. Despite its seemingly simple structure, the Rubik’s Cube presents a complex challenge due to its vast state space, consisting of approximately 4.325 × 10^19 possible states, and a small, unconstrained action space with only twelve possible actions. This complexity makes it difficult to find the shortest solution to a scrambled Rubik’s Cube using limited computational resources.
Previous research has introduced various methods to address this challenge. One notable method is DeepCubeA, which employs the A search algorithm and neural networks to find the shortest path to the solved state. Inspired by graph convolutional networks (GCNs), this paper proposes a new heuristic, weighted convolutional distance, for the A search algorithm to solve the Rubik’s Cube. This heuristic leverages the local graph structure of the cube, utilizing information from neighboring nodes and applying attention-like weights to enhance the search for the shortest path.
Basic Concepts of the Rubik’s Cube
Notations of the Rubik’s Cube
The Rubik’s Cube consists of six faces, each of which can be rotated either 90° clockwise or 90° counter-clockwise. These actions are denoted by uppercase letters for clockwise rotations and lowercase letters for counter-clockwise rotations. For example, “U” denotes rotating the up face 90° clockwise, while “f” denotes rotating the front face 90° counter-clockwise. Repeated actions are indicated with a superscript, such as “R2” for rotating the right face 180° clockwise.

Large State Space of the Rubik’s Cube
The Rubik’s Cube comprises 26 pieces, categorized into fixed pieces, corner pieces, and edge pieces. Fixed pieces are the central pieces of each face and do not influence the cube’s state. Corner pieces, located at the cube’s corners, have three face colors, while edge pieces, situated between corner pieces, have two face colors.
The number of valid permutations of the Rubik’s Cube is derived from the possible arrangements and orientations of these pieces. Considering the constraints on orientations and permutations, the total number of valid states is calculated as follows:
[ N = \frac{8! \times 3^8 \times 12! \times 2^{12}}{2 \times 3} ]
Graph Convolution on the Rubik’s Cube
Graph Representation of the Rubik’s Cube
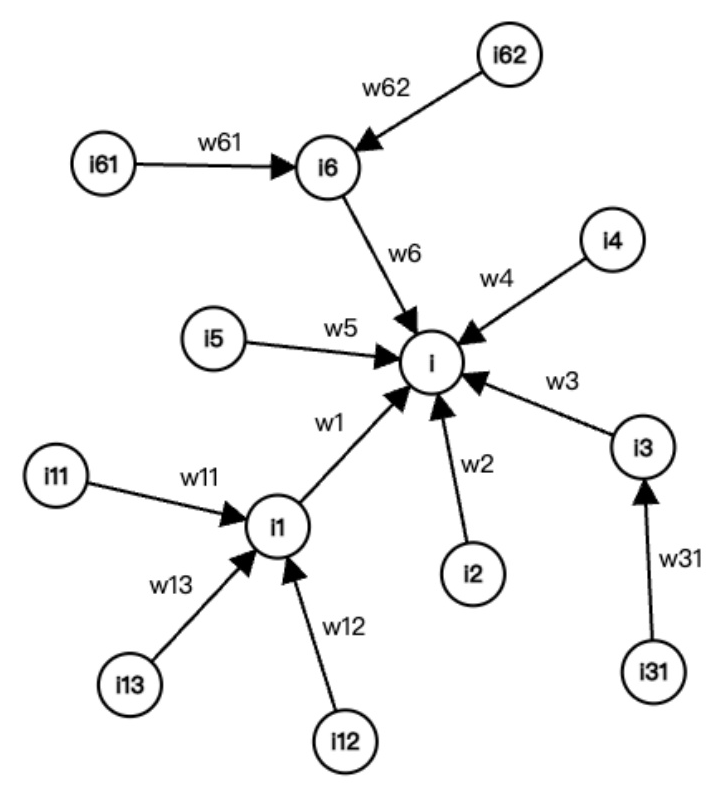
The state space of the Rubik’s Cube can be represented as a graph, where nodes correspond to cube states and edges represent actions. This representation allows the application of graph theory insights to the problem. The graph is directed, but for the purpose of this paper, an undirected representation is considered to focus on the distance from the solved state.
Representation of Nodes’ Property
Given the vast state space, storing every possible state and computing their distances from the solved state is computationally intensive. To address this, neural networks are employed to represent the value of the target property. Two neural networks are proposed: one to compute the distance from the current state to the solved state, and another to predict the next optimal move.
The distance of a state is defined as the smallest number of moves required to reach the solved state. The pre-trained model from DeepCubeA is used for distance representation, denoted as ( f_d ). Additionally, a multilayer perceptron ( f_p ) is trained to predict the probability of each possible action, providing attention-like weights for convolving the distance.
Weighted Convolutional Distance
Graph convolutional networks utilize message passing to predict graph properties by passing information between nodes and edges. Inspired by this mechanism, the weighted convolutional distance is designed to convolve a state’s distance from the solved state using action probabilities as weights. The basic formula for the weighted convolutional distance is:
[ d^{(1)}(s) = \mu f_d(s) + (1 – \mu) \sum_{A \in \text{Act}} p_{sA} f_d(s_A) ]
This formulation can be generalized for deeper convolutions:
[ d^{(k+1)}(s) = \mu d^{(k)}(s) + (1 – \mu) f_p(s)^T d^{(k)}_{\text{adj}}(s) ]
where ( d^{(k)}_{\text{adj}}(s) ) is a vector of the k-th weighted convolutional distances of the adjacent states of ( s ).
Path Search Algorithm
A* Search Algorithm for the Rubik’s Cube
The A* search algorithm is a popular heuristic for pathfinding in graphs. It classifies nodes into closed nodes (already explored) and frontier nodes (yet to be explored). The algorithm iteratively explores the node with the smallest cost estimation value, adds its neighboring nodes to the frontier list, and continues until the goal node is found.
The cost estimation function for A* search is:
[ f(n) = g(n) + h(n) ]
where ( g(n) ) is the number of actions from the initial state to the neighboring state ( n ), and ( h(n) ) is the m-layer weighted convolutional distance for some ( m \in \mathbb{N} ).
Pseudo Code
The following pseudo code outlines the A* search algorithm for solving the Rubik’s Cube:
plaintext
Algorithm 1 A* Search Algorithm for Solving the Rubik’s Cube
Input state si
s ← si
C ← {s}
F ← {adjacent states of s}
while s is unsolved do
n ← arg min n ∈ F f(n)
Add the action A taken from s' to n to the action list As' of s' ∈ C ∩ {adjacent states of n}
s ← n
C ← C ∪ {n}
F ← (F ∪ {adjacent states of n}) / S
end while
while As' is not empty do
s' ← si
Initiate the path string P
Choose the first action A in As'
Apply action A to s'
Record the action A to the P
if s' is solved then
Record the P in the path list Pl
end if
if the action list of new s' is empty then
Apply the inverse action A' to s' and delete the action A in As'
end if
end while
P' ← arg min P ∈ Pl |P|
Output P'
Result
Performance
The performance of the 1-layer and 2-layer weighted convolutional distance (WCD) heuristics was tested and compared with DeepCubeA. The evaluation parameters included average solution length, average time taken, and average number of searched nodes.
| Heuristic | Length | Time (s) | No. of Searched Nodes |
|—————-|——–|———-|———————–|
| DeepCubeA | 6.875 | 11.467 | 2938.885 |
| 1-layer WCD | 6.525 | 51.757 | 1097.345 |
| 2-layer WCD | 6.455 | 326.613 | 535.000 |
Analysis
The results indicate that the weighted convolutional distance heuristic with more convolution layers is more precise in finding a solution to the Rubik’s Cube. As the number of convolution layers increases, the average solution length and the number of searched nodes decrease, demonstrating the efficacy of this method. However, the average processing time significantly increases with deeper convolution layers due to the inability to handle the convolution process in matrix form and leverage GPUs.
Conclusion
The weighted convolutional distance heuristic provides a more precise search direction for the A* search algorithm compared to DeepCubeA, resulting in shorter solutions and fewer searched nodes. This reduces memory usage and allows for solving cubes further from the solved state. However, the current implementation is inefficient due to the lack of matrix form convolution and fast convolution techniques. Future work will focus on applying these techniques and generalizing the heuristic to other combinatorial puzzles.