Authors:
Yusong Deng、Min Wu、Lina Yu、Jingyi Liu、Shu Wei、Yanjie Li、Weijun Li
Paper:
https://arxiv.org/abs/2408.07719
Abstract
Symbolic regression aims to identify patterns in data and represent them through mathematical expressions. Traditional methods often treat variables and symbols as mere characters without considering their mathematical essence. This paper introduces the Operator Feature Neural Network (OF-Net), which employs operator representation for expressions and proposes an implicit feature encoding method for the intrinsic mathematical operational logic of operators. By substituting operator features for numeric loss, OF-Net predicts the combination of operators of target expressions. Evaluations on public datasets demonstrate superior recovery rates and high R² scores. The paper also discusses the merits and demerits of OF-Net and proposes optimization schemes.
Introduction
Deep learning and artificial intelligence have achieved significant success in various tasks, including computer vision and natural language processing. Symbolic regression, which involves extracting symbolic expressions from numerical data to map patterns, has seen foundational methods categorized into three primary directions:
- Symbolic Physics Learner (SPL): Utilizes Monte Carlo tree search to discover expressions.
- Deep Symbolic Regression (DSR): Employs reinforcement learning to guide neural networks in searching the solution space.
- Neural Symbolic Regression that Scales (NeSymReS): Leverages neural networks’ learning and fitting capabilities to generate predicted candidates end-to-end.
However, most approaches treat different operator symbols as characters of equal operational status, leading to significant numerical loss when predictions are slightly incorrect. This paper proposes OF-Net, which focuses on the mathematical operational logic of operators using implicit feature representation.
Related Work
DeepONets
Deep Operator Networks (DeepONets) consist of a trunk net and a branch net. The branch net maps the original function’s features to new features transformed by the operator, while the trunk net encodes positional features. This structure effectively approximates target functions and has been modified for specific issues in dynamic systems and partial differential equations.
Discrimination and Multimodal
Transitioning from symbolic expressions to operator architectures can be seen as a multi-target discrimination task. The transformer architecture, particularly BERT, has been widely recognized for feature extraction and processing. In symbolic regression, the set-transformer is commonly used as an encoder, capable of accepting input-output pairs and ensuring that the order of data points does not affect the outcome.
Methods
Directed Graph for Symbolic Expression Representation
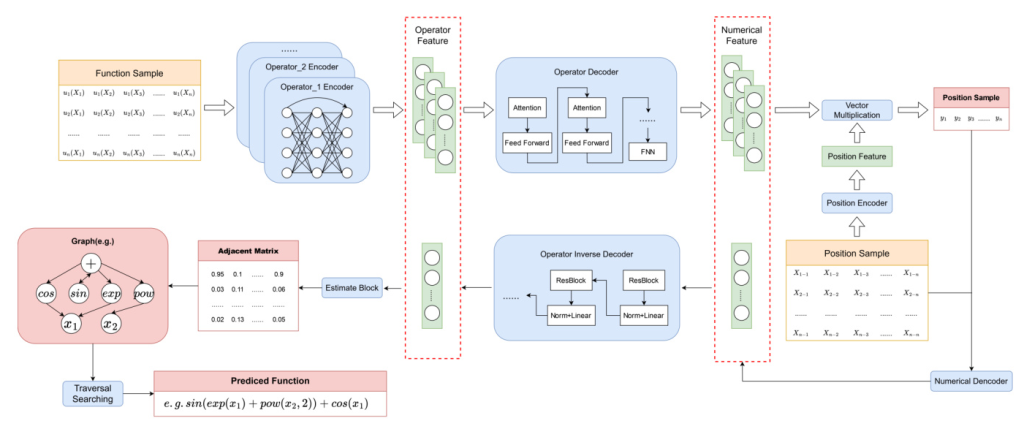
Most symbolic regression methods use tree representation, which faces issues such as multiple encodings for semantically equivalent trees and imprecise character features. OF-Net uses directed graphs where nodes are categorized into variable nodes and operator nodes. This representation reduces redundant possibilities and resolves issues encountered with tree representation.
The Network
The network structure is divided into forward fitting and backward inference. The forward network fits each operator’s computational process and captures operator features. The backward network derives the final predictive expression from the operator features. The judgment network, based on BERT, predicts the relationship between operators, and the search module constructs functions by searching paths in the operator adjacency matrix.
Searching
The search process, guided by an adjacency matrix, adopts a traversal method like breadth-first search within a constrained area. Restrictions are imposed on the nesting of operators to maintain the simplicity of expressions. Constant optimization is conducted after generating a list of candidate skeletons, using the BFGS method for optimization.
Experiments and Discussion
Conditions and Setup
The operator feature length is set at 500, numerical feature length at 200, with 200 function sampling points in the branch net and 1600 position sampling points in the trunk net. The network structure includes various blocks and layers, with hyper-parameters adjustable for scale and feature lengths.
Result
OF-Net achieved the highest recovery rate across the holistic dataset, with commendable R² outcomes. The method shows superior stability and extrapolative capabilities, particularly in univariate expressions. However, performance declines for bivariate data due to the complexity of operator structures and limitations in constant optimization.
Discussion
OF-Net’s performance varies between univariate and bivariate data. The method excels in univariate expressions but faces challenges with bivariate data due to training data limitations. Issues with operator prediction and constant optimization also impact performance. Future improvements include enriching the training dataset, revising the operator set, and proposing effective constant optimization algorithms.
Conclusion
OF-Net addresses the demerits of string prediction for tree representation in symbolic regression by using operator graphs and encoding mathematical operations into feature codes. The method achieves satisfactory performance with the highest recovery rate and excellent R² scores. Future work will focus on refining the dataset, operator set, constant optimization, and pre-processing for improved performance.