Authors:
Hendrik Alsmeier、Anton Savchenko、Rolf Findeisen
Paper:
https://arxiv.org/abs/2408.09781
Introduction
Model Predictive Control (MPC) has become a cornerstone in various industries, from autonomous driving to chemical plants, due to its flexibility and ability to handle constraints while optimizing performance. However, the computational demands of MPC can be prohibitive, especially for fast-evolving systems or those with extensive state dimensions. This paper introduces a novel approach to alleviate these computational burdens by integrating neural networks into the MPC framework, thereby enhancing efficiency without compromising safety or performance.
Related Work
Traditional MPC Approaches
MPC’s real-time feasibility can be compromised when dealing with complex systems or long prediction horizons. Traditional methods to address this include:
– Sub-optimal Solutions: Techniques like real-time iteration linearize the optimal control problem (OCP) to solve a quadratic problem, reducing computational load but potentially sacrificing optimality.
– Explicit MPC: Pre-computes control laws for linear systems with quadratic costs, but is limited by state dimensions and system linearity.
Machine Learning in MPC
Machine learning (ML) has been explored to approximate MPC control laws, reducing the need for online optimization. However, these approaches often lose explicit constraint satisfaction and optimality. Recent advancements aim to combine ML with traditional MPC, leveraging ML for parts of the control problem while retaining optimization for safety.
Research Methodology
Problem Setup
The study focuses on a discretized continuous-time nonlinear system represented by:
[ x(t_{i+1}) = f(x(t_i), u(t_i)) ]
where ( x(t_i) ) and ( u(t_i) ) are the system states and inputs at time ( t_i ), respectively. The MPC solves an OCP at each sampling point, applying the first optimal input to the system until the next sampling time.
Neural Networks
Neural networks (NNs) are employed to approximate necessary mappings due to their universal approximation capabilities. The NN structure consists of fully connected layers with hyperbolic tangent activation functions, transforming inputs to outputs through a series of affine transformations and nonlinear activations.
Experimental Design
Neural Horizon MPC
The proposed Neural Horizon MPC simplifies the OCP by approximating the state predictions over a reduced horizon using NNs. This approach replaces the tail of the optimal solution trajectory with a computationally efficient NN-based model, reducing the dependency on inputs and the number of function evaluations required during optimization.
Cost Estimation
An alternative approach involves directly approximating the cost function, mapping the state to the value function over the reduced horizon. However, this method showed discrepancies in performance compared to the state sequence approximation.
Recursive Feasibility and Constraint Satisfaction
The study ensures recursive feasibility and constraint satisfaction by generating training data that guarantees state constraints are met. This involves adapting the OCP to include error bounds and using a representative dataset for training the NNs.
Results and Analysis
Simulation Setup
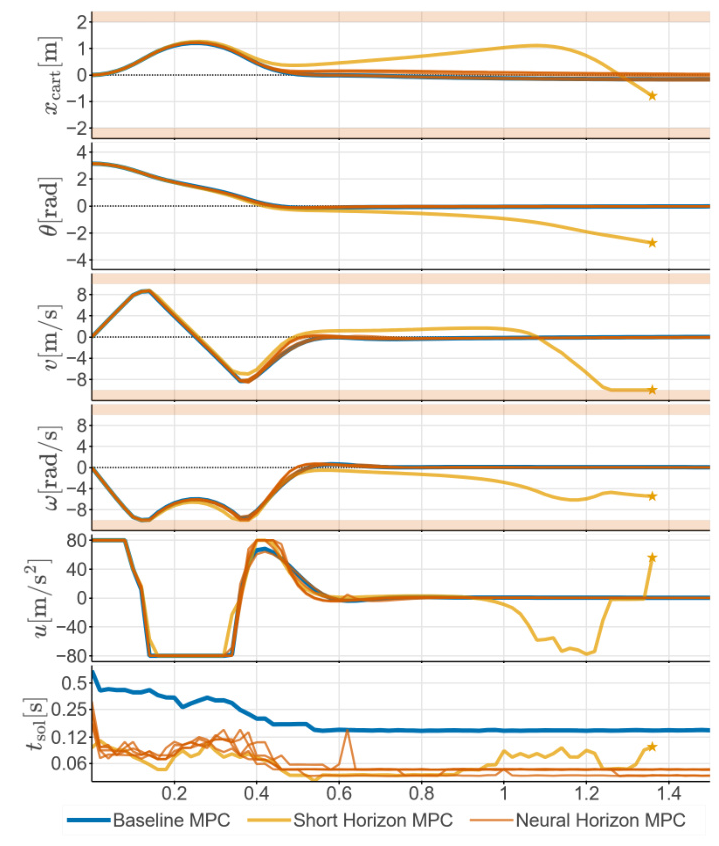
The approach is validated using an inverted pendulum on a cart model, discretized with a 20ms time step and integrated using a Runge-Kutta method. Various controllers are compared, including:
– Baseline MPC: Standard MPC with a quadratic cost function.
– Short Horizon MPC: Baseline MPC with a reduced horizon.
– Imitation Controller: NN approximating the MPC mapping.
– Neural Horizon MPC: Proposed approach with state sequence approximation.
– Cost-Estimation MPC: Direct cost estimation approach.
Performance Metrics
The controllers are evaluated based on their ability to stabilize the system, computational efficiency, and adherence to constraints. The Neural Horizon MPC demonstrated significant computational improvements while maintaining stability and constraint satisfaction.
Key Findings
- Neural Horizon MPC: Achieved near-optimal performance with reduced computational load, stabilizing the system effectively.
- Cost-Estimation MPC: Showed poor performance, indicating the complexity of directly approximating the cost function.
- Imitation Controller: Fastest computations but violated input constraints, highlighting the trade-off between speed and constraint adherence.
Overall Conclusion
The study presents a promising method to enhance MPC efficiency using neural networks. By approximating the horizon tail, the Neural Horizon MPC reduces computational demands while ensuring safety and performance. Future work will explore further optimizations and applications, including longer horizon approximations and alternative training data sources.
Illustrations
- Model Parameters:
- Inverted Pendulum System:
- State and Input Constraints:
- System Dynamics:
- Neural Network R2-Scores:
- MPC Horizon Length vs. Trajectory Cost:
- Controller Performance Comparison:
- Closed-Loop Metrics:
- Upswing of the Inverted Pendulum:
This innovative approach opens new avenues for applying MPC in resource-constrained environments, paving the way for more responsive and efficient control systems.