Authors:
Florian Grötschla、Joël Mathys、Christoffer Raun、Roger Wattenhofer
Paper:
https://arxiv.org/abs/2408.11042
Introduction
Machine learning has made significant strides in various domains, yet it still struggles with generalizing concepts and extrapolating to unseen inputs. For instance, while large language models can generate impressive text, they often fail at tasks requiring a deep understanding of algorithms, such as multiplying large numbers. This gap highlights the need for teaching machines “algorithmic thinking”—the ability to distill and apply algorithms across different situations.
Finite State Automata (FSA) represent one of the simplest forms of algorithms, transitioning between states based on predefined rules. When multiple FSAs are networked, they can achieve remarkable computational power, as exemplified by the Turing-complete Game of Life. Building on this concept, the paper introduces GraphFSA, a novel framework designed to learn FSAs on graph-structured data. GraphFSA aims to address the limitations of existing machine learning models in representing algorithmic decisions as discrete state transitions.
Related Work
Finite State Automaton (FSA)
FSAs are computational models used to describe systems operating on a finite number of states. They are widely used in fields like computer science, linguistics, and electrical engineering for tasks such as pattern recognition, parsing, and protocol specification. Recent research has explored combining FSAs with neural networks to enhance performance and generalization.
Cellular Automaton (CA)
Cellular Automata are discrete computational models consisting of a grid of cells, each in a discrete state that evolves based on the states of neighboring cells. Recent advancements include Neural Cellular Automata (NCA) and Graph Cellular Automata (GCA), which operate on graph structures with diverse neighborhood transition rules.
Graph Neural Networks (GNNs)
GNNs have gained significant attention for their ability to process graph-structured data. Various architectures, such as Graph Convolutional Networks and Graph Attention Networks, have been developed. A crucial area of GNN research is understanding their theoretical capabilities, particularly their expressiveness and interpretability.
Algorithmic Learning
Algorithmic learning aims to learn underlying algorithmic principles that allow generalization to unseen and larger instances. This involves models capable of extrapolation, particularly in graph algorithms, where the goal is to scale to more complex and larger graphs than those used during training.
Research Methodology
The GraphFSA Framework
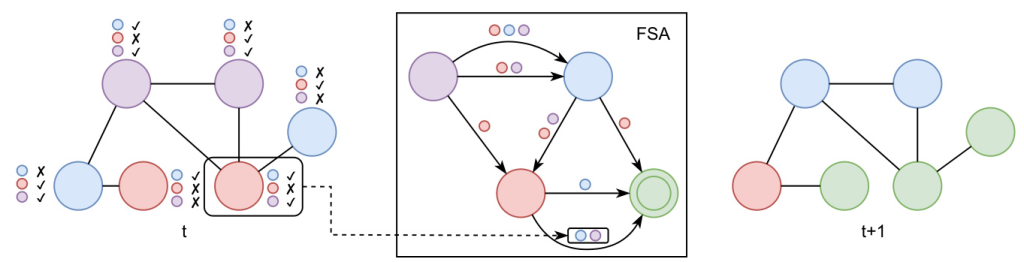
GraphFSA is designed to execute FSAs on graph-structured data. Each node in the graph runs the same FSA, which consists of a set of states and transition values. The transition values are computed through the aggregation of neighboring node states. The FSA is executed synchronously on all nodes for a fixed number of steps, resulting in each node reaching an output state.
Formal Definition
GraphFSA consists of a tuple (M, Z, A, T), where M is the set of states, Z is the set of aggregated values, A is the aggregation function, and T is the transition function. The aggregation function maps the multiset of neighboring states to an aggregated value, which, along with the current state, determines the next state transition.
Aggregation Functions
The aggregation function plays a crucial role in determining the transition values. The paper focuses on two types of aggregation: counting aggregation and positional aggregation. Counting aggregation counts the occurrences of each state in the neighborhood, while positional aggregation considers the spatial relationship between nodes.
Scalability
GraphFSA demonstrates good scalability for larger graphs, operating in linear time relative to the number of nodes and edges. However, scalability concerning the number of states is influenced by the chosen aggregation method.
Experimental Design
GRAB: The GraphFSA Dataset Generator
GRAB is a flexible dataset generator designed to evaluate learned state automatons. It generates synthetic problem instances with known ground truth, allowing for systematic benchmarking of GraphFSA models across different graph sizes and distributions.
Training Methodology
The paper proposes Diff-FSA, a specific approach to train models within the GraphFSA framework. Diff-FSA models the transition matrix as a probability distribution over possible next states, maintaining differentiability during training. The model is trained using input-output pairs, with an additional loss term to ensure iteration stability.
Baseline Models
The paper compares GraphFSA with baseline models, including Graph Neural Cellular Automata (GNCA) and recurrent message-passing GNNs. The goal is to demonstrate the value of discrete state spaces, particularly in generalizing to longer rollouts and larger graphs.
Results and Analysis
Classical Cellular Automata Problems
The paper evaluates GraphFSA on classic cellular automata problems, such as 1D and 2D automata, including Wireworld and Game of Life. The results demonstrate that GraphFSA can successfully learn the underlying automaton rules and generalize to larger grids.
Evaluation with GRAB
Using GRAB, the paper benchmarks GraphFSA on diverse datasets, including tree graphs and synthetic state automata. The results show that GraphFSA performs well across different scenarios, with strong generalization capabilities.
Graph Algorithms
The paper further evaluates GraphFSA on more challenging graph algorithm problems, such as distance computation and pathfinding. The results indicate that GraphFSA can learn correct solutions and provide interpretable representations of the learned mechanics.
Overall Conclusion
GraphFSA presents a novel framework for algorithmic learning on graphs, leveraging discrete state spaces to simulate decision-making processes. The framework demonstrates strong generalization capabilities and provides interpretable representations of learned algorithms. Future work could explore methods to map continuous input values to discrete states and investigate more finite aggregations to enhance model expressivity.
In summary, GraphFSA offers a promising approach to representing and learning graph algorithms, addressing the limitations of existing models in capturing discrete state transitions and providing explainable solutions.