Authors:
Rishabh Agrawal、Nathan Dahlin、Rahul Jain、Ashutosh Nayyar
Paper:
https://arxiv.org/abs/2408.09125
Introduction
Imitation learning (IL) has emerged as a powerful tool for robotic tasks where direct programming or defining optimal control costs is challenging. Traditional IL methods often rely on environmental interactions during learning, supplementary datasets, or knowledge of transition dynamics. However, these requirements are not always feasible in real-world scenarios, such as autonomous driving or healthcare, where safety and cost concerns limit direct interactions. This study introduces a novel approach to IL that operates under strictly batch conditions, leveraging the Markov balance equation and conditional density estimation to improve performance without additional data or interactions.
Related Work
Offline Inverse Reinforcement Learning (IRL)
Offline IRL aims to infer a reward function and recover the expert policy from a static dataset without environmental interactions. Methods like LSTD-µ, DSFN, and RCAL have been developed to address this, but they often assume complete knowledge of reward features, which is impractical for complex problems. Recent methods like IQ-Learn and CLARE incorporate conservatism in reward estimation but struggle with covariate shift and reward extrapolation errors.
Offline Imitation Learning (IL)
Energy-based models like EDM capture the expert’s state occupancy measure but face limitations in continuous action domains. DICE methods, such as ValueDICE and SoftDICE, perform stationary distribution matching but suffer from biased gradient estimates and require additional demonstration data. ODICE introduces orthogonal-gradient updates to address conflicting gradient directions but still faces challenges in strictly offline settings.
Research Methodology
The Imitation Learning Problem
The IL problem is framed within an infinite horizon discounted Markov decision process (MDP) defined by states, actions, transition functions, and policies. The objective is to develop a policy that minimizes the divergence between the expert’s and the imitator’s policies using a loss function. This study introduces a novel approach that leverages the Markov balance equation to guide learning without relying on reward model estimation or stationary distribution matching.
Normalizing Flows for Density Estimation
Conditional density estimation is crucial for the proposed IL approach. Normalizing flows (NFs) are employed due to their ability to model complex probability distributions through a sequence of invertible and differentiable transformations. This allows for precise density estimation, making NFs ideal for tasks requiring accurate probability evaluation.
Experimental Design
Markov Balance-based Imitation Learning (MBIL)
The MBIL algorithm combines policy-based and dynamics-based loss functions to enforce the Markov balance constraint. The optimization problem is formulated to minimize the discrepancy between the demonstrator’s and learner’s policies and the balance equation under the learner’s policy. The algorithm uses normalizing flows for transition density estimation and integrates dynamics loss with policy loss for effective learning.
Transition Density Estimation
Transition densities are estimated using conditional normalizing flows, which outperform other density estimation techniques in high-dimensional settings. The conditional density estimation setup involves a neural network processing the conditioning input and feeding it into coupling blocks for transformation.
Results and Analysis
Classic Control Tasks
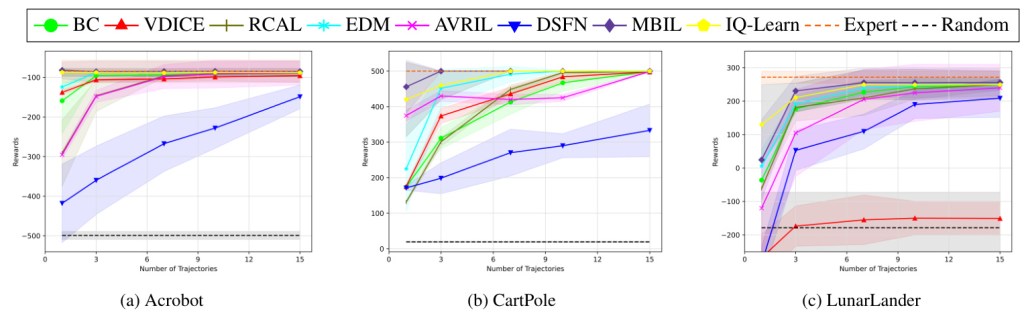
The MBIL algorithm was evaluated on Classic Control tasks like Acrobot, CartPole, and LunarLander. The results demonstrate that MBIL consistently outperforms baseline algorithms, achieving near-expert performance with limited data. The algorithm’s ability to handle distribution shifts and maintain robust performance highlights its effectiveness in strictly batch settings.
MuJoCo Tasks
In MuJoCo tasks, MBIL achieved near-expert performance with a single demonstration trajectory. The algorithm outperformed strong baselines like BC, SoftDICE, and ODICE, maintaining robust performance throughout the learning process. The integration of dynamics loss with policy loss proved crucial for effective learning in these tasks.
Ablation Study
An ablation study on the Walker2d task investigated the impact of policy loss and dynamics loss on performance. The results indicate that a combination of both losses, with a higher weight on policy loss, enables near-expert performance with minimal data.
Overall Conclusion
This study presents a novel Markov balance-based imitation learning algorithm that operates under strictly batch conditions without relying on reward model estimation or stationary distribution matching. The proposed method leverages conditional normalizing flows for density estimation and integrates dynamics loss with policy loss for effective learning. Experimental results demonstrate that MBIL outperforms state-of-the-art algorithms across various Classic Control and MuJoCo environments, handling distribution shifts more effectively. Future research could explore deriving sample complexity bounds and extending the approach to handle suboptimal data cases.