Authors:
Chunyang Jiang、Chi-min Chan、Wei Xue、Qifeng Liu、Yike Guo
Paper:
https://arxiv.org/abs/2408.09849
Introduction
Large Language Models (LLMs) have demonstrated exceptional capabilities across a wide range of natural language processing (NLP) tasks. However, fine-tuning these models using high-quality datasets under external supervision is often prohibitively expensive. To address this, self-improvement approaches for LLMs have been developed, where the models are trained on self-generated data. Despite the potential of this approach, the variability in data quality poses a significant challenge. This paper introduces a novel metric called Distribution Shift (DS) weight, inspired by Importance Weighting methods, to filter out self-generated samples with high distribution shift extent (DSE). The proposed framework, Importance Weighting-based Self-Improvement (IWSI), integrates DS weight with self-consistency to enhance the self-improvement process of LLMs.
Related Work
LLM Self-Improvement
Improving the reasoning abilities of LLMs typically requires fine-tuning on large amounts of high-quality supervised data. However, the availability of such data is limited, leading to the exploration of self-improvement methods. These methods involve generating data using the LLM itself and then fine-tuning the model on this self-generated data. The primary challenge here is the variability in data quality, which necessitates effective data filtering strategies. Previous works have employed various filtering techniques, such as majority voting for self-consistency and entropy-based filtering to exclude high-uncertainty data points.
Importance Weighting
Importance Weighting (IW) is a well-established approach to address distribution shift problems. It involves estimating importance weights based on the distribution ratio between test and training data and using these weights to build an unbiased training loss. Traditional IW methods have been effective in linear models but face challenges in deep learning scenarios. Recent advancements, such as Dynamic Importance Weighting (DIW), propose end-to-end solutions using deep networks to predict importance weights iteratively.
Research Methodology
Overview of IWSI
The IWSI framework consists of several key components:
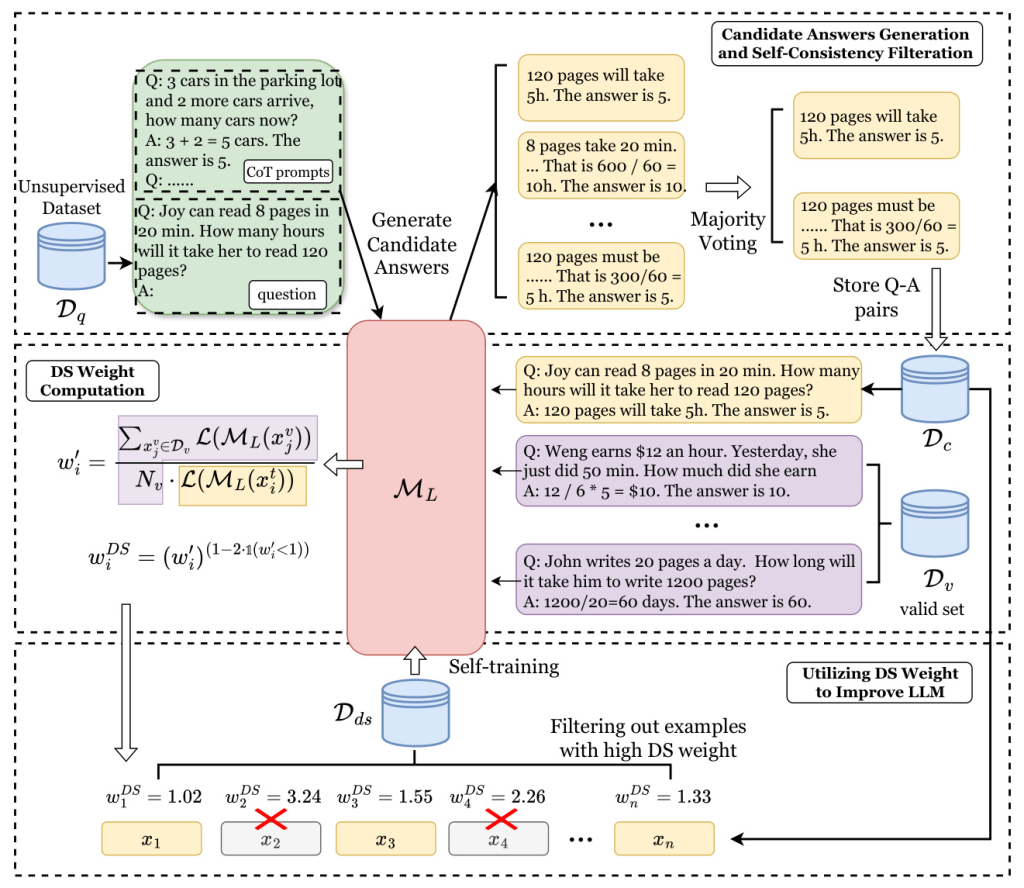
- Candidate Answers Generation and Self-Consistency Filtration: The pre-trained LLM generates multiple candidate answers and reasoning thoughts for each question in an unsupervised dataset. Majority voting is used to select the most consistent answer and corresponding thoughts, resulting in a consistency-filtered dataset.
- DS Weight Computation: DS weight is computed for each data point in the consistency-filtered dataset using a tiny valid set. This weight measures the distribution shift extent (DSE) of self-generated samples.
- Filtering and Fine-Tuning: The dataset is further filtered based on DS weight, retaining samples with the lowest DS weight. The model is then fine-tuned on this filtered dataset.
Candidate Answers Generation and Self-Consistency Filtration
Given an unsupervised dataset, the pre-trained LLM generates multiple candidate answers and reasoning thoughts for each question using Chain-of-Thought (CoT) prompts. Majority voting is employed to select the most consistent answer and corresponding thoughts, forming the consistency-filtered dataset.
DS Weight Computation
DS weight is computed using a valid set and the pre-trained LLM. The weight estimation process involves calculating the importance weights based on the distribution shift between the training samples and the valid set. The DS weight is then used to rank the samples, with higher weights indicating greater distribution shift.
Utilizing DS Weight to Improve LLM
The dataset is filtered by retaining samples with the lowest DS weight, ensuring that samples with high distribution shift are excluded. The model is then fine-tuned on this filtered dataset, enhancing its reasoning abilities.
Experimental Design
Datasets
Experiments were conducted on six datasets across three types of tasks: arithmetic reasoning (gsm8k, SVAMP), natural language inference (ANLI-A1, ANLI-A2), and commonsense reasoning (OpenBookQA, StrategyQA). Only the questions were used to generate candidate answers, and a tiny valid set was created for each dataset.
Baselines
The performance of IWSI was compared with several baseline self-improvement methods, including LMSI, Entropy-filter, Self-filter, and RM-filter. These baselines employ different filtering strategies to improve the quality of self-generated data.
Implementation Details
The experiments were conducted using the Llama3-8B model. The model generated 15 candidate answers for each question, and the training process was performed on eight RTX-4090 GPUs. The learning rate was set to 3e-4, and LoRA was used for fine-tuning.
Results and Analysis
Main Results
The results showed that IWSI consistently outperformed the baseline self-improvement methods across all datasets. The incorporation of DS weight significantly enhanced the effectiveness of LLM self-improvement, particularly in arithmetic reasoning tasks.
Hyperparameter Study
The impact of varying the filtering threshold was investigated, revealing that an optimal threshold exists for each task. Generally, a threshold around 80% was found to be appropriate.
Valid Set Analysis
The composition of the valid set plays a crucial role in the stability of DS weight computation. The results indicated that the impact of different valid set compositions on accuracy was minimal, demonstrating the robustness of the IWSI framework.
Orthogonality Analysis
The relationship between answer correctness and DS weight was explored, revealing a degree of independence between these factors. The analysis suggested that DS weight is nearly orthogonal to other factors, such as answer uncertainty.
Perception of DSE
A case study on the gsm8k dataset provided insights into the characteristics of samples with high DSE. These samples were categorized into redundant, jumping, and spurious samples, highlighting the importance of filtering out such samples to improve model performance.
Overall Conclusion
This paper introduced a novel metric, DS weight, to approximate the distribution shift extent of self-generated data in LLMs. The proposed IWSI framework effectively integrates DS weight with self-consistency to filter out high DSE samples, significantly enhancing the self-improvement process of LLMs. The empirical results demonstrated the efficacy of this approach, suggesting a new direction for future research in LLM self-improvement.