Authors:
Paper:
https://arxiv.org/abs/2408.08336
Graph Representations of 3D Data for Machine Learning
Abstract
This paper provides an overview of combinatorial methods to represent 3D data, such as graphs and meshes, from the perspective of their suitability for analysis using machine learning algorithms. It highlights the advantages and disadvantages of various representations and discusses methods for generating and switching between these representations. The paper also presents two concrete applications in life science and industry, emphasizing the practical challenges and potential solutions.
Introduction
3D data is prevalent in various scientific and industrial domains, including bioimaging, molecular chemistry, and 3D modeling. While 3D representations offer a more accurate depiction of real-world objects compared to 2D projections, they come with significant computational challenges. The extra dimension and the inherent sparsity of 3D data make it difficult to apply learning algorithms that scale effectively. This paper explores whether these challenges can be mitigated by using lighter representations of 3D data, such as graphs, meshes, point clouds, and simplicial complexes, along with corresponding deep learning algorithms. The findings suggest that in many real-world situations, these lighter representations can be beneficial.
3D Data
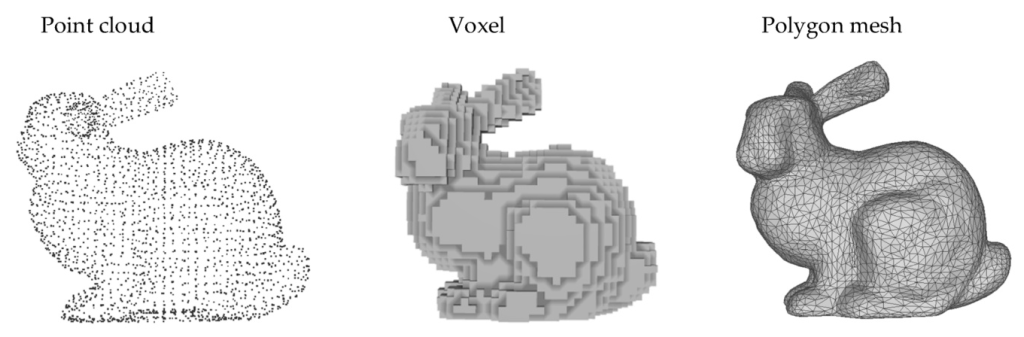
Volumetric
The primary challenge with 3D data compared to 2D data is the computational complexity of the algorithms required for analysis. The most common representation of 3D data is by voxels, which are the 3D equivalent of pixels. This representation results in a dense grid of 3D cubes, each storing information such as RGB color or intensity. The number of voxels grows exponentially with the dimension, leading to severe computational requirements. Additionally, 3D data is often sparse, with the actual object of interest occupying only a small portion of the volume. This sparsity, combined with the high computational cost, makes the analysis of 3D data challenging.
Mesh
A mesh is a tessellation of a 3D object’s surface using triangles or other polygons. It effectively describes geometry and addresses the sparsity problem by only storing the positions of vertices and the connections between them. Meshes do not have a global coordinate system but resemble a local coordinate system around each vertex. This allows the use of techniques for processing 2D images, appropriately adjusted for 3D data. However, meshes are constrained to representing surfaces of 3D manifolds, which can be limiting for highly non-smooth or non-manifold data.
Point Cloud
A point cloud is a collection of points in 3D space, described by their coordinates and additional features such as RGB color or intensity. Point clouds offer flexibility and some structure of Euclidean data. However, they often lack geometric information, as there are no apparent relations between the points. Point clouds can be very large, but subsampling can address this issue, allowing different granularity for different parts of the object.
Graphs
Graphs are a versatile representation for 3D data, balancing expressiveness and simplicity. They can be defined abstractly by specifying vertices and edges, often carrying spatial and geometric information. Graphs can represent various structures, such as skeletal graphs for human poses or knowledge graphs for social networks. Graph Neural Networks (GNNs) are well-suited for analyzing graph data, offering scalability, ease of engineering, and flexibility in enriching or transforming the graph.
The ‘2-step Process’ in Graph Analysis
To leverage GNNs and other graph-related tools, 3D data must first be converted into a graph format. This involves generating a graph from the original representation, followed by analyzing the graph itself. Standard methods for graph generation include converting meshes to graphs by taking the 1-skeleton, converting voxels to graphs by connecting neighboring voxels, and converting point clouds to graphs based on vertex proximity.
Graph Generation Methods
The paper investigates skeletonization methods, which produce a 1-dimensional skeleton of a 3D shape, capturing global geometric information. These methods include signed distance function thinning, Medial Axis Transform, and machine learning-inspired approaches like SN-graph.
Analysis Methods
Graph Neural Networks (GNNs) are the default choice for graph data analysis. GNNs apply filters at the vertex level and aggregate information from neighbors to update vertex states. They offer flexibility in designing graph networks and can incorporate standard neural network components. Simpler approaches, such as vertex embeddings or using graph features for classical models, can also be effective.
Applications in Concrete Cases
Mitochondrial Networks in Muscle Cells
Bioimaging and preclinical research often involve large, sparse, and scarce 3D data. This section presents a case study on analyzing mitochondrial networks in muscle cells using graph representations.
Data
The data consists of confocal fluorescent microscopy images of muscle cells, with one channel showing mitochondrial networks. The images are manually labeled on a scale from 1 to 10 by an expert annotator.
Task
The task is to predict the healthiness of mitochondrial networks, posed as either a binary classification (healthy/unhealthy) or a regression on a scale of 1 to 10. Healthiness is associated with conditions such as primary carnitine deficiency, obesity, physical inactivity, and type 2 diabetes.
Method
Given the intuition behind the healthiness of cells, a graph representation is used to encode the images, capturing the connectedness and geometric shape of the grid. The images are cut into patches, and graphs are generated using a skeletonization algorithm. A Graph Attention Network (GAT) is used for classification and regression, with vertex and edge attributes including geometric features and image intensity.
AI for 3D Design Generation and Analysis
This section presents findings from a pilot project with RD8 Technology, focusing on analyzing 3D design drawings for manufacturing.
Data
The data consists of parametric 3D geometries, which are challenging to analyze using 3D convolutional neural networks due to varying scales and high resolution. Instead, the data is represented as polygonal meshes and then converted to graphs.
Task
The task is to calculate the contact areas between interconnected parts in a 3D design. This involves predicting the contact areas based on a target mask provided by RD8’s software.
Method
The parts are represented as triangular meshes and converted to graphs. The task becomes a binary semantic segmentation of vertices, predicting whether each vertex is part of a contact area. A Graph Attention Network (GAT) is used for this task, with additional edges and vertex normal vectors added to the graph to capture proximity and orientation.
Conclusion
The paper demonstrates that graph representations of 3D data can effectively address the computational challenges associated with 3D data analysis. By leveraging combinatorial methods and deep learning algorithms, it is possible to achieve accurate and efficient analysis in various real-world applications. The findings suggest that practitioners of machine learning can benefit from adopting these methods in their work with 3D data.