Authors:
Antonio Almudévar、Alfonso Ortega、Luis Vicente、Antonio Miguel、Eduardo Lleida
Paper:
https://arxiv.org/abs/2408.07016
Introduction
Representation learning aims to discover and extract factors of variation from data. A representation is considered disentangled if it separates these factors in a way that is understandable to humans. Traditional definitions and metrics for disentanglement assume that factors of variation are independent, which is often not the case in real-world scenarios. This paper proposes a new definition of disentanglement based on information theory, valid even when factors of variation are not independent. The authors also relate this definition to the Information Bottleneck Method and propose a method to measure disentanglement under these conditions.
Related Work
Definition and Properties of Disentanglement
Disentangled representations separate different factors of variation in data. Early evaluations relied on visual inspection, but more precise definitions and metrics are needed. One widely accepted definition states that a disentangled representation changes one factor of variation while being invariant to others. However, this definition and others have limitations, especially when factors of variation are not independent.
Metrics for Measuring Disentanglement
Metrics for measuring disentanglement fall into three categories:
- Intervention-based Metrics: Create subsets with common factors of variation and compare their representations.
- Information-based Metrics: Estimate mutual information between factors of variation and representation variables.
- Predictor-based Metrics: Train regressors or classifiers to predict factors of variation from representation variables.
Methods to Obtain Disentangled Representations
Most initial methods for achieving disentangled representations were unsupervised, often modifying Variational Autoencoders (VAEs) or using Generative Adversarial Networks (GANs). However, unsupervised disentanglement is challenging without inductive biases. Supervised methods, which use labels to indicate factors of variation, have been proposed as an alternative.
Defining Disentanglement for non-Independent Factors of Variation
Problem Statement
In representation learning, raw data ( x ) is explained by factors of variation ( y ) and nuisances ( n ). Factors of variation are conditionally independent given ( x ). A representation ( z ) is described by ( p(z|x) ), and the goal is to separate factors of variation into ( z ).
Properties of Disentanglement
The paper redefines the properties of disentanglement from an information theory perspective:
- Modularity: A variable ( z_j ) is modular if it captures at most one factor of variation ( y_i ), considering dependencies between factors.
- Compactness: A variable ( z_j ) is compact if it is the only one capturing a factor of variation ( y_i ), considering dependencies.
- Explicitness: A representation is explicit if it contains all information about its factors of variation.
Connection to Information Bottleneck
The Information Bottleneck method aims to balance accuracy and complexity in representations. A representation is sufficient if it maximizes information about the task and minimal if it minimizes information about the input. The paper shows that satisfying sufficiency and minimality guarantees disentanglement.
Measuring Disentanglement for non-Independent Factors of Variation
The authors propose methods to measure modularity, compactness, and explicitness, considering dependencies between factors of variation.
Modularity
To measure modularity, the authors train regressors to predict ( z_j ) from ( y_i ) and ( y ), then compute the difference in predictions. The procedure is detailed in Algorithm 1.
Compactness
Compactness is measured by training regressors to predict ( y_i ) from ( z_j ) and ( z ), then computing their difference. The procedure is detailed in Algorithm 2.
Explicitness
Explicitness is measured by training a regressor to predict ( y_i ) from ( z ) and comparing the prediction to the actual ( y_i ).
Experiment I: Cosine Dependence
The authors create controlled scenarios with known relationships between factors of variation and representation variables. They compare their proposed metrics with others in the literature.
Modularity
The results show that traditional metrics fail to detect modularity when factors of variation are dependent, while the proposed metric does not have this problem.
Compactness
The proposed metric maintains its value even when factors of variation are dependent, unlike traditional metrics.
Explicitness
The proposed metric correlates well with traditional metrics but also captures the difficulty of obtaining factors of variation from the representation.
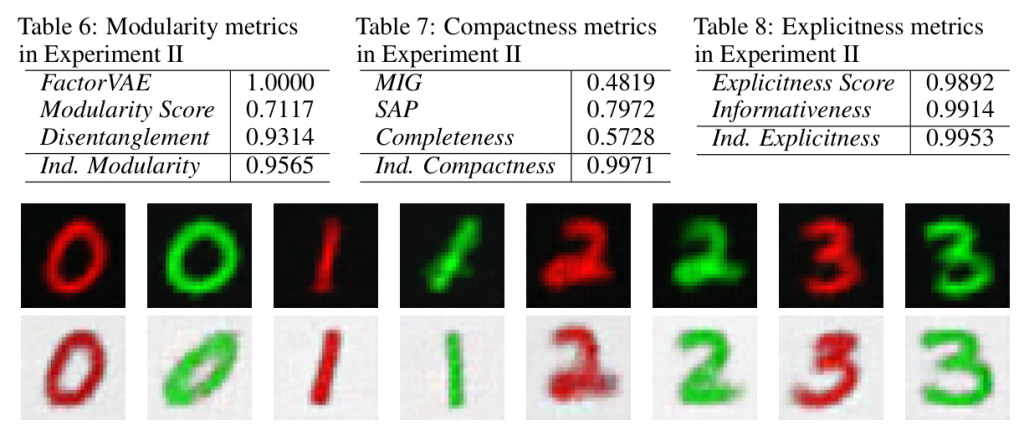
Experiment II: Conditionally Colored MNIST
The authors design a dataset with dependent factors of variation and train a VAE to achieve disentanglement. They demonstrate that traditional metrics fail to detect disentanglement, while their proposed metrics do not.
Modularity
The proposed metric correctly identifies modularity, while traditional metrics do not.
Compactness
The proposed metric correctly identifies compactness, while traditional metrics do not.
Explicitness
All metrics agree that the representation captures all factors of variation.
Conclusion
The paper presents a new definition of disentanglement that considers dependencies between factors of variation. The authors propose methods to measure disentanglement under these conditions and demonstrate their effectiveness through experiments. Their approach overcomes the limitations of traditional metrics and provides a more accurate assessment of disentanglement in real-world scenarios.