Authors:
Zhiqiang Wang、Xinyue Yu、Qianli Huang、Yongguang Gong
Paper:
https://arxiv.org/abs/2408.08909
Introduction
In the era of big data, privacy concerns have become paramount, especially with the advent of federated learning (FL). Introduced by Google in 2016, federated learning allows multiple clients to collaboratively train a machine learning model without sharing their raw data. This decentralized approach mitigates privacy risks and reduces communication complexity. However, even though raw data is not exchanged, the computed results can still leak sensitive information. Differential privacy (DP) is a common technique used to address these privacy concerns in federated learning. However, traditional DP methods with fixed privacy budgets often compromise model accuracy. This paper proposes an adaptive differential privacy method based on federated learning, aiming to balance privacy protection and model accuracy by dynamically adjusting the privacy budget.
Related Work
Differential Privacy in Federated Learning
Since 2017, various methods have been proposed to enhance privacy in federated learning using differential privacy:
- User-Level Differential Privacy: Geyer et al. (2017) introduced algorithms that average client models and use randomization to protect individual contributions. However, this method’s performance is highly dependent on the number of clients.
- Long Short-Term Memory (LSTM): McMahan et al. (2018) improved user-level privacy by implementing LSTM, but required pre-designed scaling factors, posing practical challenges.
- Bayesian Differential Privacy: Triastcyn et al. (2019) proposed DP-FedAvg, which provided differential privacy guarantees but required significant computational resources.
- Adaptive Privacy-Preserving Federated Learning (APFL): Liu et al. (2020) introduced a framework that adaptively injected noise based on localized differential privacy, but incurred additional costs.
- Model Perturbation: Yang et al. (2021) proposed adding random noise during model parameter transmission to defend against reconstruction and membership inference attacks.
- Two-Layer Privacy Protection: Ouadrhiri et al. (2022) reduced dataset dimensionality and applied differential privacy to the compressed dataset, achieving good accuracy but dependent on dataset compression.
- Gradient Compression Framework: Chen et al. (2022) introduced a framework with adaptive privacy budget allocation, balancing security, accuracy, and communication efficiency.
- Adaptive Privacy Budget Strategy: Zhang (2022) adjusted the privacy budget based on cosine similarity but lacked consideration for accuracy and loss.
- Functional Mechanisms: Cao et al. (2023) replaced perturbed gradients with perturbed objective functions, but gradients still contained privacy information.
- Adaptive Differential Privacy Federated Learning: Tang (2023) used a scoring function to reduce noise but did not discuss adjustment coefficients.
- Adaptive Clipping: Wang et al. (2023) proposed a framework that adaptively selected gradient clipping thresholds, but uniformly allocated privacy budgets, leading to unnecessary waste.
Research Methodology
Methodology Overview
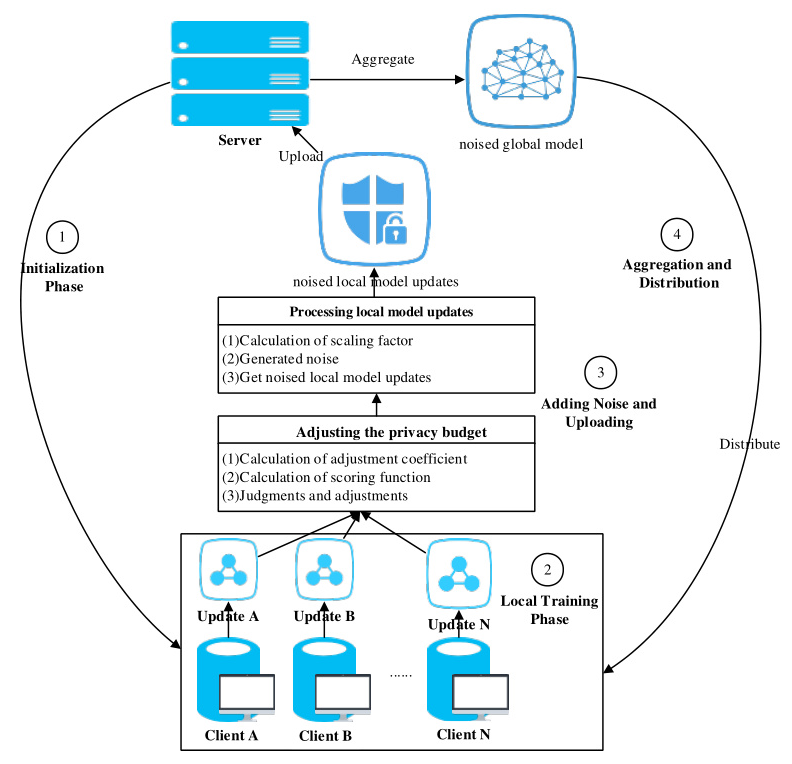
The proposed adaptive differential privacy method, termed cosAFed, consists of four stages: initialization, local training, adding noise and uploading, and aggregation and distribution. The process is illustrated in Figure 1.
Adjusting the Privacy Budget
The core of the proposed method is the dynamic adjustment of the privacy budget. The adjustment involves three steps:
- Calculation of Adjustment Coefficient: Based on the cosine similarity between the local and global models, the number of datasets, and the number of clients.
- Calculation of Scoring Function: Considers accuracy, loss, and training rounds.
- Judgments and Adjustments: Adjusts the privacy budget based on the calculated coefficients and scores.
The detailed algorithm is presented in Algorithm 2.
Process of Local Model Updates
The local model updates involve three steps:
- Calculation of Scaling Factor: Based on cosine similarity.
- Generated Noise: Using Laplace distribution.
- Noised Local Model Updates: Adding noise to the local model updates before uploading.
Experimental Design
Experimental Environment
The experiments simulate a federated learning environment with one server and 100 clients, using the MNIST dataset and a logistic regression model. The experimental setup is detailed in Table 1.
Experimental Parameters
The experiments are divided into Equal and Random groups based on different data partitioning methods. The specific parameters are shown in Table 2.
Results and Analysis
Accuracy
The training results for the Equal and Random groups with different numbers of selected clients are shown in Figures 2 and 3. Both groups exhibit an upward trend in accuracy and a downward trend in loss, indicating model convergence.
Increasing the number of selected clients generally leads to more stable accuracy curves and higher best accuracy (best_acc), as shown in Figures 4 and 5. However, in some cases, the added noise may slightly reduce accuracy.
Privacy Budget
The privacy budget results for different initial budgets and numbers of selected clients are shown in Figures 6 and 7. The privacy budget reverts to the initial value after being reduced, ensuring data availability and model accuracy.
Comparison with Other Methods
The proposed cosAFed method is compared with LAPFed, ADPFL, and cosFed. The results, shown in Table 3 and Figures 8 and 9, indicate that cosAFed requires the least total privacy budget while maintaining comparable accuracy.
Overall Conclusion
The proposed adaptive differential privacy method based on federated learning dynamically adjusts the privacy budget according to multiple factors, enhancing data protection while ensuring model accuracy. Experimental results show that cosAFed reduces the privacy budget by about 16% compared to other methods, with minimal impact on accuracy. Future work will explore more suitable calculation methods and other implementation mechanisms, such as the Gaussian mechanism, to further validate the method’s feasibility.