Authors:
Baekryun Seong、Jieung Kim、Sang-Ki Ko
Paper:
https://arxiv.org/abs/2408.10900
Introduction
Artificial Intelligence (AI) research has recently been dominated by large language models (LLMs), which have demonstrated significant improvements in performance with increased parameters. However, this scaling comes with a substantial increase in power consumption, leading to environmental concerns such as carbon emissions and climate change. Spiking Neural Networks (SNNs) offer a promising alternative due to their event-driven nature, mimicking the human brain and significantly reducing power consumption compared to traditional artificial neural networks (ANNs).
Despite their potential, SNNs face challenges in terms of reliability and robustness, particularly against adversarial attacks. Current methods for verifying the stability and properties of SNNs are time-consuming and lack scalability. This paper introduces a novel approach using temporal encoding to enhance the efficiency of formal verification of SNNs, making it feasible to verify SNNs at scales previously deemed impractical.
Related Work
Formal Verification of Neural Networks
Formal verification of neural networks is crucial for ensuring their robustness, especially in safety-critical applications. There are two primary methods for verification: abstraction-based and constraint-based. Abstraction-based methods approximate neural networks using abstract interpretation theory, while constraint-based methods use satisfiability modulo theories (SMT) solvers to verify properties.
Previous works have extended the simplex method for neural networks with ReLU activation functions and introduced frameworks like Marabou for piecewise-linear activation functions. However, these methods are not directly applicable to SNNs due to their discrete and temporal nature.
Mathematical Modeling of SNNs
SNNs differ significantly from ANNs due to their event-driven and time-varying characteristics. Researchers have proposed formalizations of SNNs using timed automata and SMT-based encoding for adversarial robustness verification. However, these methods have limited scalability and are computationally expensive.
Information Encoding in SNNs
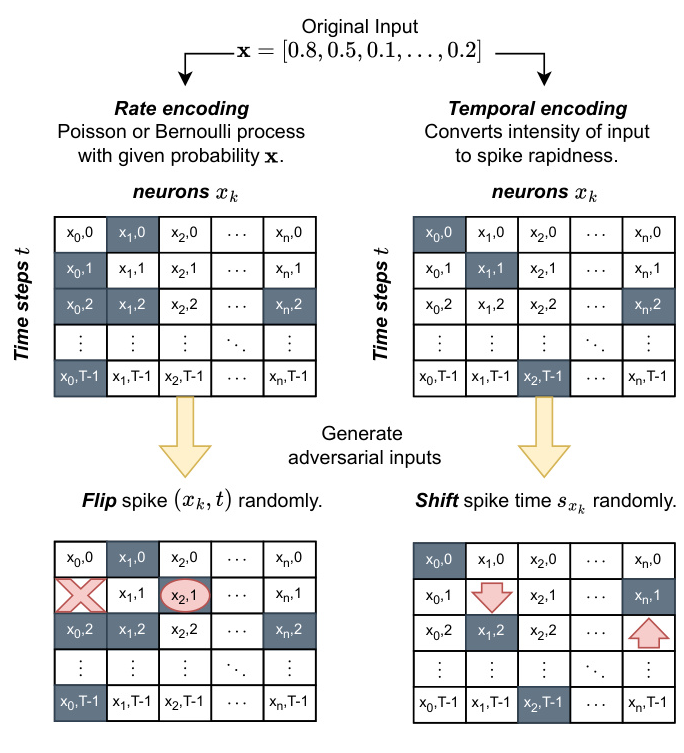
SNNs can encode input data using rate encoding, temporal encoding, or delta modulation. Rate encoding interprets input size as the probability of spiking, while temporal encoding forces each input neuron to spike once, with larger inputs spiking faster. Temporal encoding is more power-efficient but harder to train.
Adversarial Robustness in SNNs
Adversarial robustness is critical for practical applications of neural networks. Various methods have been proposed to enhance the robustness of SNNs, including robust training algorithms and conversion techniques from ANNs to SNNs.
Research Methodology
SMT Encoding of Temporal Encoded SNN
The proposed method encodes the mathematical behavior and adversarial robustness conditions of SNNs using quantifier-free linear real arithmetic formulas. This encoding allows for sound and complete verification of SNNs.
Theoretical Analysis
The paper provides a theoretical comparison of the proposed temporal encoding with previous SMT encodings based on rate encoding. The analysis demonstrates an exponential reduction in the perturbation space, making the verification process more efficient.
Direct Counterexample Search (DCS)
To address the inefficiency of SMT solvers, the paper proposes a Direct Counterexample Search (DCS) algorithm. This algorithm directly generates the perturbation set and checks for adversarial counterexamples, significantly reducing verification time.
Experimental Design
Experimental Setup
Experiments were conducted using the MNIST and FashionMNIST datasets. The verification process involved models with varying numbers of hidden neurons and time steps. The experiments aimed to balance practicality and ease of verification.
Verification Time Analysis
The experiments compared verification times for different numbers of hidden neurons and time steps. The results showed that temporal encoding significantly reduced verification times compared to rate encoding. The DCS algorithm further improved verification efficiency.
Results and Analysis
Verification Time with Different Numbers of Hidden Neurons
Temporal encoding demonstrated significantly lower verification times compared to rate encoding, even with an increasing number of hidden neurons. This result aligns with the theoretical prediction that perturbation space does not depend on the number of hidden neurons.
Verification Time with Different Time Steps
Temporal encoding performed well even with a higher number of time steps, contrary to the theoretical prediction. The DCS algorithm further reduced verification times, making the process more efficient.
Comparison of Verification Methods
The comparison of verification methods showed a substantial gap between temporal encoding and rate encoding, with the DCS algorithm providing the most efficient verification times.
Overall Conclusion
The paper presents a novel approach to the formal verification of SNNs using temporal encoding and the DCS algorithm. The key contributions include an exponential reduction in perturbation space and improved verification efficiency. While the study achieved significant progress, further research is needed to address the training difficulty of temporal SNNs and to experiment with more complex datasets and network architectures.
Illustrations
-
Figure 1: The mechanism of SNN. The Spike train of the previous layer, which consists of 0 and 1, is multiplied with weights and integrated together. The integrated value is added to potential, which decays with time.
! -
Figure 2: Two ways to encode inputs in SNNs.
! -
Figure 3: MNIST Examples of the original input image (left) and the image with temporal perturbation (right) where ∆= 4.
! -
Figure 4: Verification runtime with different numbers of time steps (left) and different numbers of hidden neurons (right) at MNIST and FashionMNIST dataset.
! -
Figure 5: DCS Verification runtime with different numbers of time steps (left) and different numbers of hidden neurons (right) at MNIST dataset, with different ∆s.
! -
Table 1: Experimental results of robustness verification on two models with different numbers of hidden neurons with ∆= 1. Values are given as mean ± standard deviation.
!