Authors:
Damiano Azzolini、Elisabetta Gentili、Fabrizio Riguzzi
Paper:
https://arxiv.org/abs/2408.08732
Introduction
Statistical Relational Artificial Intelligence (StarAI) is a subfield of AI that focuses on describing complex probabilistic domains using interpretable languages. Examples of such languages include Markov Logic Networks, Probabilistic Logic Programs, and Probabilistic Answer Set Programs (PASP). This paper addresses the task of parameter learning within PASP, which involves tuning the probabilities of facts in a probabilistic logic program to maximize the likelihood of observed interpretations.
The authors propose two algorithms for parameter learning in PASP:
1. An algorithm that uses an off-the-shelf constrained optimization solver.
2. An algorithm based on the Expectation Maximization (EM) algorithm.
Empirical results demonstrate that these proposed algorithms often outperform existing approaches in terms of solution quality and execution time.
Background
Answer Set Programming
An answer set program consists of normal rules of the form:
[ h \leftarrow b_0, \ldots, b_m, \text{not } c_0, \ldots, \text{not } c_n ]
where ( h ), the ( b_i )’s, and the ( c_i )’s are atoms. The semantics of an answer set program is based on the concept of a stable model, often called an answer set.
Probabilistic Answer Set Programming
Probabilistic Answer Set Programs (PASP) extend answer set programs with probabilistic facts of the form ( p :: a ), where ( p ) is the probability associated with the atom ( a ). The Credal Semantics (CS) is used to define the probability of a query in PASP, which involves computing lower and upper bounds for the probability.
Example
Consider a simple graph reachability problem encoded in PASP:
prolog
0.2::edge(1,2).
0.3::edge(2,4).
0.9::edge(1,3).
path(X,Y) :- connected(X,Z), path(Z,Y).
path(X,Y) :- connected(X,Y).
connected(X,Y) :- edge(X,Y), not nconnected(X,Y).
nconnected(X,Y) :- edge(X,Y), not connected(X,Y).
The probability of the query path(1, 4) can be computed by considering all possible worlds and their probabilities.
Parameter Learning in Probabilistic Answer Set Programs
Parameter learning in PASP involves finding the probability assignment to probabilistic facts that maximizes the likelihood of observed interpretations. This task can be formulated as an optimization problem where the goal is to maximize the log-likelihood of the interpretations.
Algorithms for Parameter Learning
Extracting Equations from a NNF
The upper probability of a query can be represented as a nonlinear symbolic equation. This equation can be extracted from a Negation Normal Form (NNF) representation of the query.
Solving Parameter Learning with Constrained Optimization
The first proposed algorithm casts the parameter learning task as a constrained nonlinear optimization problem. The steps involved are:
1. Extract the equation for the probability of each interpretation from the NNF.
2. Simplify the equation.
3. Set up and solve the constrained optimization problem using an off-the-shelf solver.
Solving Parameter Learning with Expectation Maximization
The second proposed algorithm uses the Expectation Maximization (EM) algorithm. The steps involved are:
1. Extract equations for the probabilities of queries.
2. Iteratively perform the expectation and maximization steps until convergence.
Related Work
Several tools and techniques exist for parameter learning in probabilistic logic programs, such as PRISM, EMBLEM, and ProbLog2. However, few tools consider PASP and allow multiple models per world. The proposed algorithms are compared against PASTA, a solver that uses projected answer set enumeration.
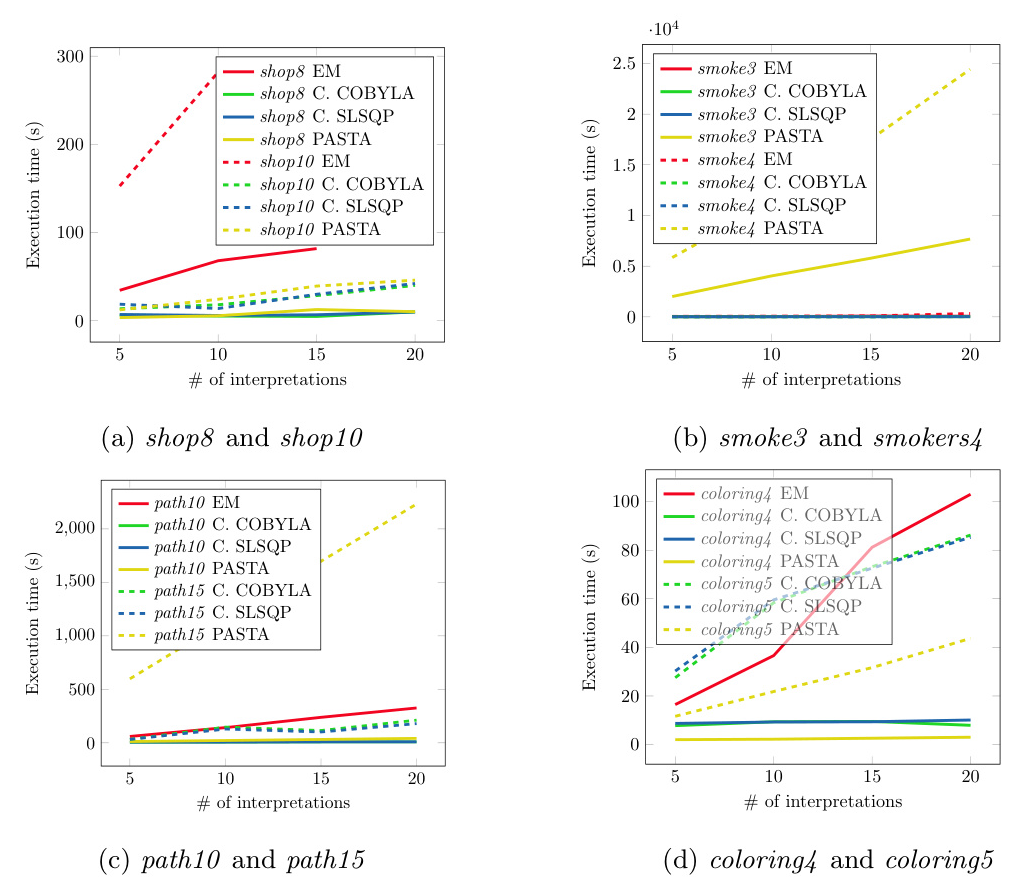
Experiments
The experiments were conducted on a computer with 16 GB of RAM and a time limit of 8 hours. The goals of the experiments were to:
1. Compare the execution times of the algorithms.
2. Evaluate the quality of the solutions in terms of log-likelihood.
3. Assess the impact of different initial probability values on execution time.
4. Compare the proposed algorithms against PASTA.
Datasets Descriptions
Four datasets were used in the experiments:
1. Coloring: Models the graph coloring problem.
2. Path: Models a path reachability problem.
3. Shop: Models shopping behavior with constraints on product purchases.
4. Smoke: Models a network where people are influenced by the smoking behavior of their friends.
Results
The results show that the algorithms based on constrained optimization (COBYLA and SLSQP) are faster and more accurate than the EM-based algorithm and PASTA. The initial probability values have little influence on the execution time for SLSQP but have a more significant impact on COBYLA.
Conclusions
The paper proposes two algorithms for parameter learning in PASP, one based on constrained optimization and the other on Expectation Maximization. Empirical results show that the constrained optimization algorithms are more accurate and faster than the EM-based algorithm and PASTA. Future work includes considering parameter learning for other semantics and studying the complexity of the task.
This blog post provides a detailed overview of the paper “Symbolic Parameter Learning in Probabilistic Answer Set Programming,” explaining the key concepts, proposed algorithms, related work, experimental setup, and results. The illustrations included help to visualize the concepts and results discussed.