Authors:

Marianela Morales、Alberto Pozanco、Giuseppe Canonaco、Sriram Gopalakrishnan、Daniel Borrajo、Manuela Veloso

Paper:

https://arxiv.org/abs/2408.10889

Learning Action Costs from Input Plans: A Comprehensive Analysis

Introduction

In the realm of classical planning, the primary objective is to devise a sequence of deterministic actions that transition an initial state to a goal state. Traditionally, the focus has been on learning the dynamics of actions—how actions change the state—while assuming that the cost associated with each action is known. However, in many real-world applications, the cost of actions is either unknown or only approximately known. This paper introduces a novel problem: learning the costs of actions such that a set of input plans are optimal under the resulting planning model. The proposed solution, LACFIPk, aims to learn these costs from unlabeled input plans, providing both theoretical and empirical evidence of its effectiveness.

Related Work

Learning Action Models

Most existing research in automated planning focuses on learning the dynamics of actions from input plans. These works aim to generate valid plans by understanding how actions change the state. However, they often overlook the importance of learning action costs, which are crucial for ranking and optimizing plans. Notable exceptions include NLOCM and LVCP, which learn both action dynamics and costs but require each plan to be annotated with its total cost.

Inverse Reinforcement Learning

Inverse Reinforcement Learning (IRL) involves inferring the reward function of an agent based on observed behavior. While IRL shares similarities with learning action costs, it typically operates within the framework of Markov Decision Processes (MDPs) and assumes a single reward function for all observations. In contrast, the problem addressed in this paper involves multiple goals and does not require such assumptions.

Research Methodology

Problem Definition

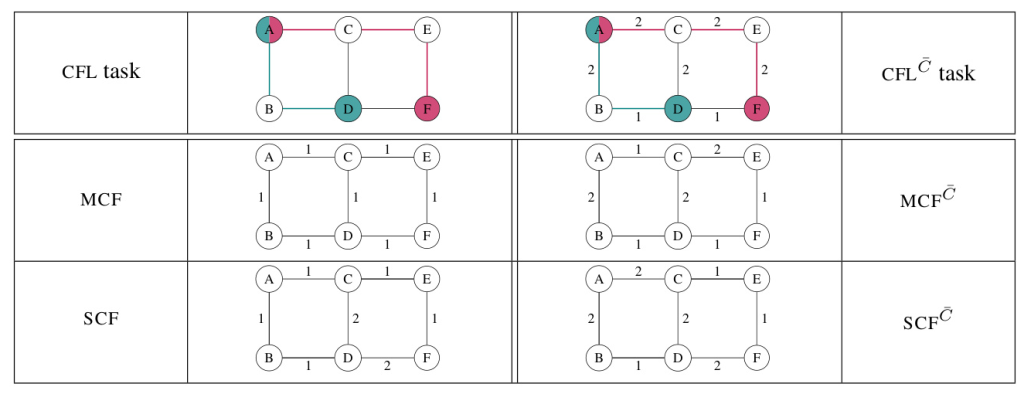
The problem of learning action costs is formally defined as a Cost Function Learning Task (CFL), where the goal is to find a common cost function for a sequence of planning tasks and their corresponding plans. The objective is to align the action costs with the input plans to generate new plans that better reflect observed behavior.

Solution Concepts

The paper introduces several solution concepts:
– Ideal Cost Function (ICF): A cost function under which all input plans are optimal.
– Maximal Cost Function (MCF): A cost function that maximizes the number of input plans that are optimal.
– Strict Cost Function (SCF): A cost function under which the input plans are the only optimal plans.
– Cost Function Refinement Task (CFL ¯ C): Refining an existing approximate cost function using observed plans.

Experimental Design

Benchmark Domains

Experiments were conducted in four planning domains: BARMAN, OPENSTACKS, TRANSPORT, and GRID. For each domain, 50 different problems were generated by varying the initial and goal states. A pool of 5,000 tuples (planning tasks and their corresponding plans) was created for each domain.

Evaluation Metrics

The performance of LACFIPk was evaluated based on the ratio of plans made optimal. The execution time of the algorithm was also analyzed to assess its scalability.

Results and Analysis

Performance Analysis

LACFIPk consistently outperformed the baseline algorithm, with its performance improving as the number of alternative plans (k) increased. The ratio of plans turned optimal tended to saturate with lower k values, indicating that good results could be achieved without computing many alternatives. However, as the size of the planning tasks grew, LACFIPk’s scalability was challenged, particularly in more complex domains like BARMAN and TRANSPORT.

Execution Time Analysis

The execution time of LACFIPk increased with the size of the CFL tasks and the number of alternative plans. While the baseline algorithm returned cost functions in less than 10 seconds, LACFIPk’s execution time varied significantly, with higher k values leading to longer computation times.

Overall Conclusion

This paper introduces a novel approach to learning action costs from input plans, addressing a critical gap in the field of automated planning. The proposed algorithm, LACFIPk, demonstrates the ability to learn cost functions that align with observed behavior, generating plans that better reflect real-world preferences. While the algorithm shows promise, future work will focus on improving its scalability and extending its applicability to handle suboptimal plans and plans with additional annotations.

References

• Aineto, Celorrio, and Onaindia (2019)
• Arora et al. (2018)
• Behnke and Bercher (2024)
• Choi and Kim (2012)
• Cresswell, McCluskey, and West (2013)
• Forrest and Lougee-Heimer (2005)
• Garrido (2023)
• Garrido and Gragera (2024)
• Gregory and Lindsay (2016)
• Helmert (2006)
• Kambhampati (2007)
• Lanchas et al. (2007)
• Michini and How (2012)
• Nebel, Dimopoulos, and Koehler (1997)
• Ng, Russell et al. (2000)
• Pozanco et al. (2023)
• Salerno, Fuentetaja, and Seipp (2023)
• Seipp, Torralba, and Hoffmann (2022)
• Speck, Mattmüller, and Nebel (2020)
• Yang, Wu, and Jiang (2007)