Multi-View Neural Differential Equations for Continuous-Time Stream Data in Long-Term Traffic Forecasting

Authors:

Paper:

Introduction

Long-term traffic flow forecasting is essential for intelligent transportation systems, enabling traffic managers to make informed decisions well in advance. However, accurately predicting traffic flow over extended periods is challenging due to the complex spatio-temporal correlations and dynamic patterns present in continuous-time stream data. Traditional Neural Differential Equations (NDEs) have shown promise in modeling continuous-time traffic dynamics but fall short in long-term forecasting due to their inability to capture delayed traffic patterns, dynamic spatial dependencies, and abrupt trend shifts.

To address these limitations, the authors propose a novel architecture called Multi-View Neural Differential Equations (MNDE). This model captures current states, delayed states, and trends in different state variables (views) by learning latent multiple representations within NDEs. Extensive experiments on real-world traffic datasets demonstrate that MNDE outperforms state-of-the-art models in long-term forecasting accuracy and robustness against noisy or missing inputs.

Preliminaries and Problem Statement

Preliminaries

Flow Rate Measurements: Traffic flow at various locations is measured using sensors, resulting in a flow-rate measurement matrix. This matrix is interpolated into continuous time functions using the natural cubic spline method.

Neural Differential Equation (NDE): NDEs, including Neural Ordinary Differential Equations (NODE) and Neural Controlled Differential Equations (NCDE), are used to model continuous-time dynamics. These methods train neural networks to approximate gradient functions, capturing the evolution of latent variables over time.

Problem Statement

The goal is to design a deep learning network, MNDE, that takes past traffic measurements over a set number of intervals and forecasts future flow rates over a longer period. The objective is to minimize the error between the predicted and actual flow rates.

Related Works on Traffic Forecasting

Statistics and Machine Learning Approaches

Traditional methods like ARIMA, SARIMA, and KNN focus on temporal dependencies but often neglect spatial factors, limiting their effectiveness in capturing complex traffic patterns.

Deep Learning Approaches

Deep learning models, such as DCRNN, STGCN, GraphWaveNet, and others, have been developed to capture spatio-temporal dependencies. However, these models often struggle with long-term forecasting due to their limited ability to capture dynamic patterns and dependencies.

Neural Differential Equation Methods

NDEs optimize neural networks using differential equations, allowing for continuous depth and high-capacity function approximation. Recent models like STGODE and STGNCDE have applied NDEs to traffic forecasting, but they still fall short in capturing delayed and abrupt traffic patterns.

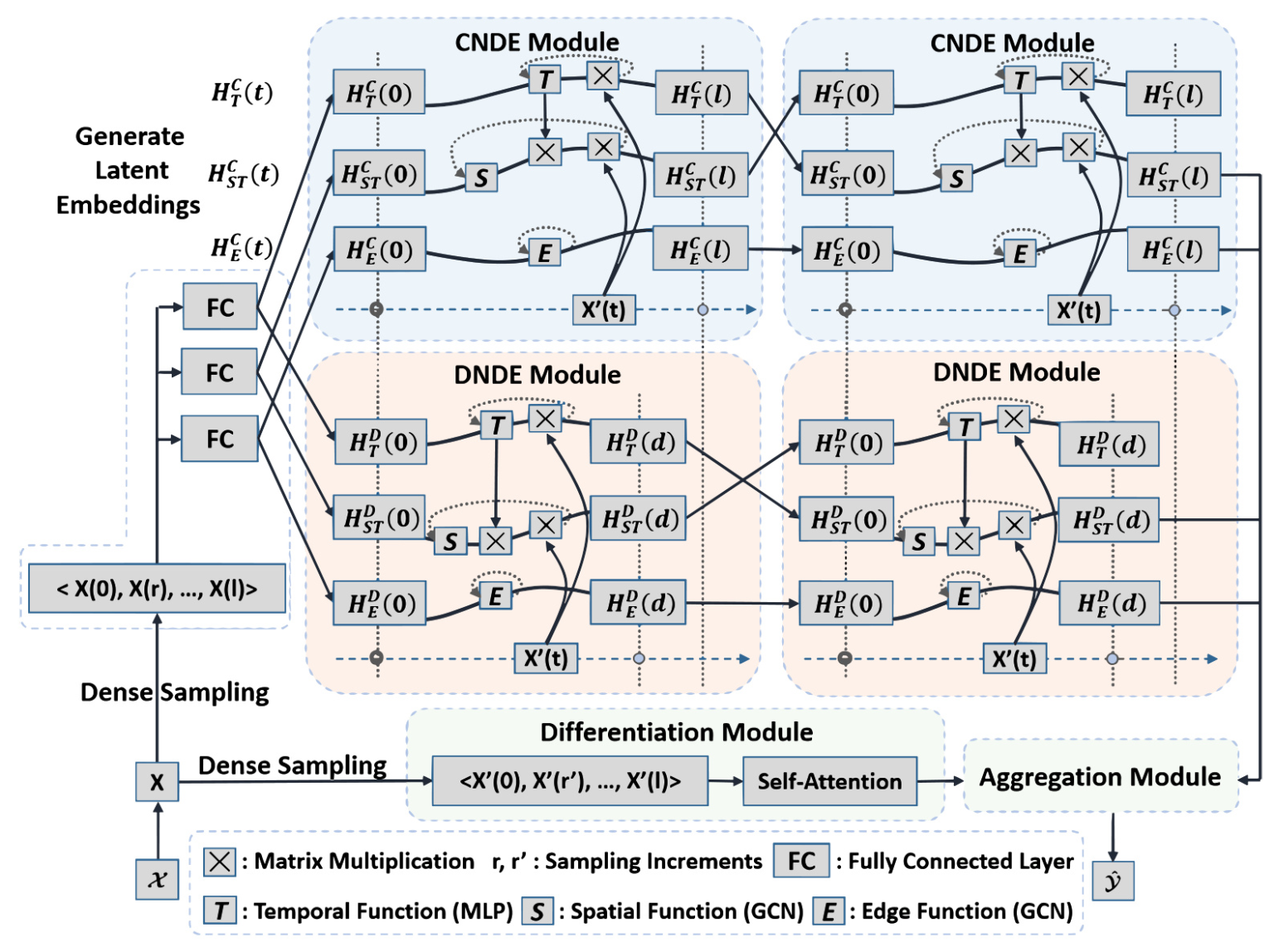
Proposed Approach

The MNDE framework consists of several modules designed to capture different aspects of traffic dynamics:

Temporal Interpolation and Latent Embeddings

Discrete flow-rate measurements are interpolated into continuous time functions and densely sampled. These samples are fed into fully connected layers to generate embeddings for temporal dynamics, spatio-temporal dynamics, and dynamic edge interactions.

Current Neural Differential Equations (CNDE) Module

The CNDE module includes three NDEs for temporal dynamics, spatio-temporal dynamics, and dynamic edge patterns. Each NDE captures different aspects of the traffic flow, with the temporal function incorporating temporal information, the spatial function capturing spatial dependencies, and the edge function modeling dynamic edge interactions.

Delayed Neural Differential Equations (DNDE) Module

The DNDE module extends the CNDE module by incorporating delayed factors in temporal integration, capturing delayed temporal dynamics, spatio-temporal dynamics, and edge interactions. This module addresses the delayed propagation of traffic conditions.

Differentiation Module

This module captures abrupt shift patterns in traffic flow by conducting self-attention on temporal gradients. It focuses on fine-grained analysis to capture nuanced fluctuations and interactions.

Aggregation Module

The final latent embeddings from the CNDE, DNDE, and differentiation modules are aggregated to make the long-term flow rate forecast. This aggregation technique allows for the selection of critical forecasting features and non-linear aggregation.

Experiments and Numerical Results

Settings and Datasets

The authors use five public traffic flow datasets (PEMS03, PEMS04, PEMS08, PEMS-BAY, and METR-LA) for evaluation. The datasets are pre-processed using z-score normalization and split into training, validation, and testing subsets. The experiments are conducted on a server with high computational resources.

Model Performance

The MNDE model demonstrates superior performance compared to state-of-the-art models across multiple datasets and forecasting horizons. It significantly improves accuracy, especially in long-term forecasting scenarios.

Ablation Study

Ablation experiments show that the DNDE module and the differentiation module contribute the most to reducing forecast errors. The edge dynamics and the looping of the CNDE module also improve accuracy, highlighting the importance of capturing delayed propagation and local traffic trends.

Robustness Study

The robustness of MNDE is evaluated by introducing missing data and noise into the input measurements. The model exhibits strong robustness, with performance degrading modestly even with high levels of missing data and noise.

Different Length of Input Data

The performance of MNDE is compared with other models using varying lengths of input data. MNDE consistently outperforms other models, demonstrating its ability to capture traffic dynamics effectively.

Delayed Pattern Visualization

The impact of the DNDE and CNDE modules is visualized, showing the temporal shift in traffic dynamics and confirming the importance of delayed dynamics in improving forecasting performance.

Results Under Different Flow Rate Ranges

The forecasting error of MNDE and STGNCDE is compared across different flow rate ranges. MNDE performs better in every range, demonstrating its effectiveness in capturing traffic patterns across varying conditions.

Robustness with Zeros

An additional robustness study is conducted by injecting noise into the input data, replacing original values with zeros. MNDE outperforms baseline models even with high levels of noise, highlighting its robustness.

Prediction Variance

The variance in MNDE’s performance across different random seeds is minimal, and it consistently outperforms other models across different datasets.

Efficiency and Scalability

The trade-off between RMSE performance and inference time is analyzed. While MNDE has a larger inference time, it delivers superior RMSE performance, making it suitable for use cases where accuracy is critical. The model’s inference time scales with dataset size, demonstrating its scalability.

Conclusion

The MNDE framework addresses several challenges in long-term traffic forecasting by modeling delayed propagation, capturing spatial dependencies, and handling local abrupt shifts in traffic trends. Extensive experiments demonstrate its superior performance compared to state-of-the-art models. The proposed approach offers a robust and accurate solution for long-term traffic flow forecasting, making it a valuable tool for intelligent transportation systems.

Acknowledgement

The authors acknowledge the support from the National Science Foundation and the National Institute of Health for their research.

Illustrations:

Overview of the MNDE framework
Basic statistics of the datasets used in the experiments
Performance comparison of models on PEMS03 dataset
Performance comparison of models on PEMS04 and PEMS08 datasets
Robustness comparison of models on PEMS08 dataset
Comparison of traffic flow forecasting between MNDE and STGNCDE on PEMS04 dataset
Ablation study results on PEMS08 dataset
Forecasting error under different flow rate ranges on PEMS08 dataset
Performance comparison of models with different lengths of input data on PEMS04 dataset
Flow rate distribution on PEMS08 dataset
Embedding visualization of CNDE and DNDE modules
Inference time comparison of MNDE across datasets of varying sizes
Robustness comparison of models with noise on PEMS08 dataset
RMSE and inference time trade-off for various methods on PEMS08 dataset
Performance comparison on PEMS-BAY dataset