Authors:
Ziming Liu、Pingchuan Ma、Yixuan Wang、Wojciech Matusik、Max Tegmark
Paper:
https://arxiv.org/abs/2408.10205
Introduction
In recent years, the intersection of artificial intelligence (AI) and science has led to significant advancements in various fields, such as protein folding prediction, automated theorem proving, and weather forecasting. However, a major challenge remains: the inherent incompatibility between AI’s connectionism and science’s symbolism. To address this, the paper “KAN 2.0: Kolmogorov-Arnold Networks Meet Science” proposes a framework that synergizes Kolmogorov-Arnold Networks (KANs) with scientific discovery. This framework aims to bridge the gap between AI and science by incorporating scientific knowledge into KANs and extracting scientific insights from them.

Related Work
Kolmogorov-Arnold Networks (KANs)
KANs are inspired by the Kolmogorov-Arnold representation theorem (KART), which states that any continuous high-dimensional function can be decomposed into a finite composition of univariate continuous functions and additions. Unlike traditional multi-layer perceptrons (MLPs), KANs feature learnable activation functions on edges, allowing for the decomposition of high-dimensional functions into one-dimensional functions. This property enhances interpretability by enabling symbolic regression of these 1D functions.
Machine Learning for Physical Laws
Previous research has shown that machine learning can be used to learn various types of physical laws, including equations of motion, conservation laws, symmetries, and Lagrangian and Hamiltonian mechanics. However, making neural networks interpretable often requires domain-specific knowledge, limiting their generality. KANs aim to evolve into universal foundation models for physical discoveries.
Mechanistic Interpretability
Mechanistic interpretability seeks to understand how neural networks operate at a fundamental level. Some research focuses on designing models that are inherently interpretable or proposing training methods that explicitly promote interpretability. KANs fall into this category, as they decompose high-dimensional functions into a collection of 1D functions, which are significantly easier to interpret.
Research Methodology
MultKAN: Augmenting KANs with Multiplications
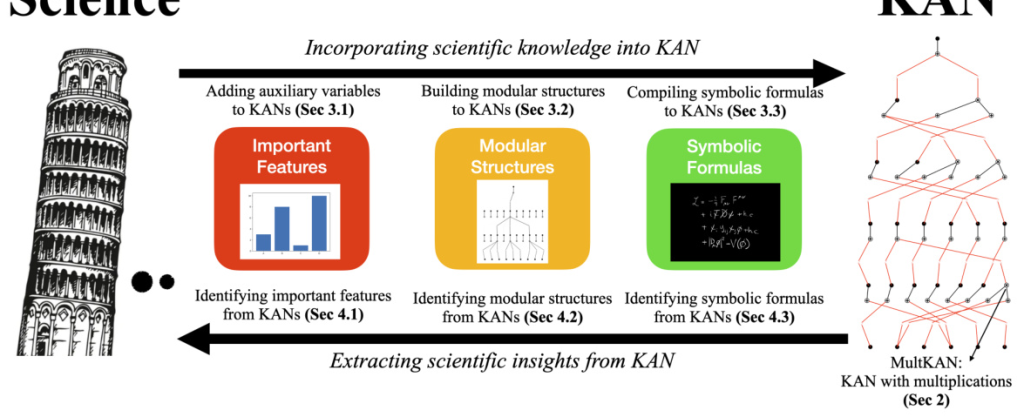
The paper introduces MultKAN, an extension of KANs that includes multiplication nodes. This enhancement allows KANs to reveal multiplicative structures in data more clearly, improving both interpretability and capacity. The MultKAN framework is mathematically defined and illustrated, showing how it can learn to use multiplication nodes effectively.
Incorporating Scientific Knowledge into KANs
The paper explores three types of inductive biases that can be integrated into KANs:
- Important Features: Adding auxiliary input variables to increase the expressive power of the neural network.
- Modular Structures: Enforcing modularity by introducing the module method, which preserves intra-cluster connections while removing inter-cluster connections.
- Symbolic Formulas: Compiling symbolic equations into KANs and fine-tuning these KANs using data.
Extracting Scientific Knowledge from KANs
The paper proposes methods to extract scientific knowledge from KANs at three levels:
- Important Features: Introducing an attribution score to better reflect the importance of variables.
- Modular Structures: Uncovering modular structures by examining anatomical and functional modularity.
- Symbolic Formulas: Using symbolic regression to extract symbolic formulas from KANs.
Experimental Design
Identifying Important Features
The paper introduces an attribution score to identify important variables in a regression model. This score is computed iteratively from the output layer to the input layer, providing a more accurate reflection of variable importance than the L1 norm.
Identifying Modular Structures
The paper explores anatomical and functional modularity in neural networks. Anatomical modularity is induced through neuron swapping, while functional modularity is detected by examining separability, generalized separability, and generalized symmetry.
Compiling Symbolic Formulas
The kanpiler (KAN compiler) converts symbolic formulas into KANs. This process involves parsing the symbolic formula into a tree structure, modifying the tree to align with the KAN graph structure, and combining variables in the first layer.
Results and Analysis
Discovering Conserved Quantities
The paper demonstrates the use of KANs to discover conserved quantities in a 2D harmonic oscillator. The KANs successfully identify the three conserved quantities: energy along the x direction, energy along the y direction, and angular momentum.
Discovering Lagrangians
KANs are used to learn Lagrangians for a single pendulum and a relativistic mass in a uniform field. The results show that KANs can effectively learn the correct Lagrangian functions, with symbolic regression successfully identifying the underlying formulas.
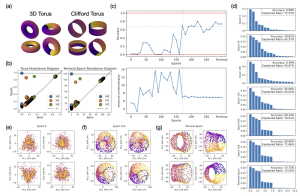
Discovering Hidden Symmetry
The paper revisits the problem of discovering the hidden symmetry of the Schwarzschild black hole using KANs. The results show that KANs can achieve extreme precision by refining the grid, demonstrating their potential for high-precision scientific discovery.
Learning Constitutive Laws
KANs are used to predict the pressure tensor from the strain tensor in Neo-Hookean materials. The results show that KANs can accurately predict the constitutive laws, with symbolic regression identifying the correct formulas.
Overall Conclusion
The paper “KAN 2.0: Kolmogorov-Arnold Networks Meet Science” presents a comprehensive framework for integrating KANs with scientific discovery. By incorporating scientific knowledge into KANs and extracting scientific insights from them, the framework bridges the gap between AI’s connectionism and science’s symbolism. The proposed methods and tools demonstrate the potential of KANs for various scientific tasks, including discovering conserved quantities, Lagrangians, hidden symmetries, and constitutive laws. The paper highlights the importance of interpretability and interactivity in AI tools, paving the way for future research in AI-driven scientific discovery.