Authors:
Rujia Shen、Boran Wang、Chao Zhao、Yi Guan、Jingchi Jiang
Paper:
https://arxiv.org/abs/2408.08023
Introduction
Causal discovery from time-series data is essential for understanding the relationships among variables over time. This understanding is crucial for various scientific disciplines, such as medicine and economics. Traditional methods for causal discovery from non-time-series data are not directly applicable to time-series data due to the need for serialized samples and a larger number of observed time steps.
To address these challenges, the authors propose a novel gradient-based causal discovery approach called STIC (Short-Term Invariance-based Convolutional causal discovery). STIC leverages convolutional neural networks (CNNs) to uncover causal relationships by focusing on short-term time and mechanism invariance within each observation window. This approach enhances sample efficiency and accuracy in causal discovery from time-series data.
Background
Symbol Summarization
The paper provides a table summarizing the symbols and their definitions used throughout the study. This table helps in understanding the mathematical notations and concepts discussed in the subsequent sections.
Problem Definition
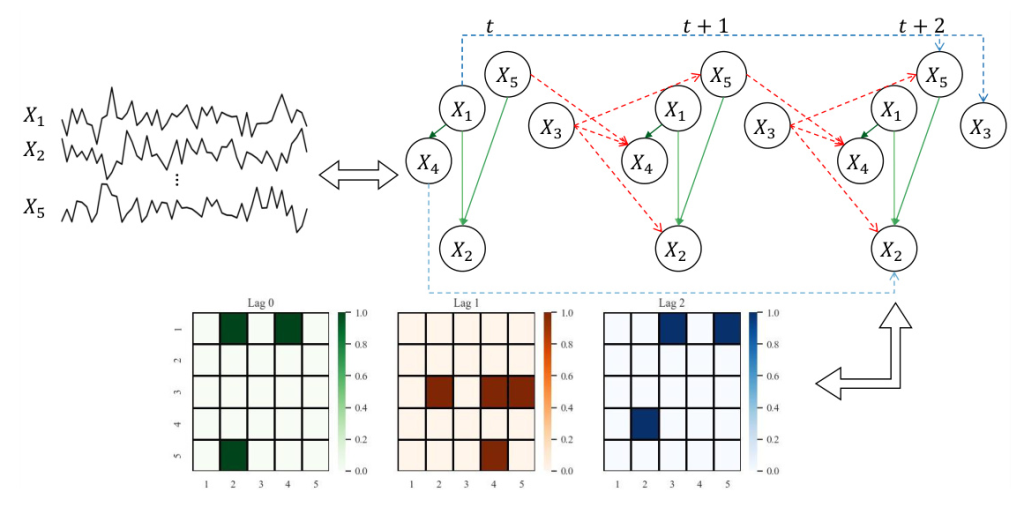
The objective of causal discovery from time-series data is to uncover the underlying window causal graph, which represents both intra-slice (contemporaneous) and inter-slice (time-lagged) causality. The window causal graph is defined as a finite Directed Acyclic Graph (DAG) with nodes representing observed variables and edges representing causal relationships with time lags.
Short-Term Causal Invariance
The authors introduce two forms of short-term invariance: time invariance and mechanism invariance. These invariances are fundamental assumptions in causal discovery from time-series data.
- Short-Term Time Invariance: The parent-child relationships between variables remain consistent over short periods.
- Short-Term Mechanism Invariance: The conditional probability distributions of causal effects between variables remain constant over short periods.
Necessity of Convolution
The authors establish the equivalence between convolution operations and the underlying generative mechanism of time-series data. This theoretical grounding justifies the use of convolutional neural networks in the STIC framework for causal discovery.
Granger Causality
Granger causality is an autoregressive approach to causal discovery that assesses if one time series can predict another. This method is used as a baseline for comparison with the proposed STIC approach.
Method
The STIC framework consists of four main components: Window Representation, Time-Invariance Block, Mechanism-Invariance Block, and Parallel Blocks for Joint Training.
Window Representation
The observed dataset is transformed into a window representation format using a sliding window approach. This transformation helps in capturing both contemporaneous and time-lagged causal relationships within each window.
Time-Invariance Block
The time-invariance block captures the causal relationships among variables by leveraging a convolutional neural network structure. This block extracts shared information from the window representation to obtain the estimated window causal matrix.
Mechanism-Invariance Block
The mechanism-invariance block identifies the numerical transform functions in the window causal graph. It uses another convolutional kernel to transform the window observations and predict the future values of the target variables.
Parallel Blocks for Joint Training
The outputs from the time-invariance and mechanism-invariance blocks are combined to predict the observed dataset. The model is optimized using the Mean Squared Error (MSE) loss between the predicted and actual values.
Experiment Results
The authors conduct experiments on both synthetic and benchmark datasets to evaluate the performance of STIC. The results demonstrate that STIC outperforms baseline methods in terms of F1 score and precision, particularly when dealing with limited observed time steps.
Baselines
The study compares STIC with six state-of-the-art causal discovery methods: PCMCI, PCMCI+, DYNOTEARS, TCDF, CUTS, and CUTS+. These methods represent different approaches to causal discovery, including constraint-based, score-based, and Granger-based methods.
Experiments on Synthetic Datasets
The authors generate synthetic datasets with linear and non-linear relationships to evaluate the performance of STIC. The results show that STIC achieves higher F1 scores and precision compared to the baselines, especially in scenarios with limited observed time steps.
Experiments on Benchmark Datasets
The authors use the FMRI benchmark dataset to explore brain blood flow patterns. The results indicate that STIC achieves the highest average F1 scores and precision compared to the baselines, demonstrating its practical value in real-world applications.
Ablation Study
The ablation study investigates the impact of different hyper-parameters on the performance of STIC. The results show that the learning rate has little effect on the model’s performance, while the predefined maximum time lag and threshold significantly influence the F1 score and precision.
Discussion
Effectiveness of STIC
The study highlights the effectiveness of STIC in discovering causal relationships from time-series data. The use of short-term invariance and convolutional neural networks enhances sample efficiency and accuracy in causal discovery.
Exceptional Performance
The incorporation of window representation, time-invariance block, and mechanism-invariance block contributes to the high F1 scores and precision achieved by STIC. These components enable the model to learn accurate causal structures and complex non-linear transformations.
Conclusion, Limitations, and Future Works
The paper introduces STIC, a novel method for causal discovery from time-series data. The experimental results demonstrate the efficiency and stability of STIC, particularly in scenarios with limited observed time steps. However, the study acknowledges certain limitations, such as the assumption of additive noise and the manual predefined maximum lag. Future research should aim to develop more comprehensive approaches capable of handling various types of noise and explore advanced blocks to enhance the performance of STIC.
Acknowledgments
The study was supported by grants from the National Key Research and Development Program of China and the National Natural Science Foundation of China.