Authors:
Dona Arabi、Jafar Bakhshaliyev、Ayse Coskuner、Kiran Madhusudhanan、Kami Serdar Uckardes
Paper:
https://arxiv.org/abs/2408.10951
Introduction
Time series forecasting (TSF) is a critical task in various domains such as finance, healthcare, and manufacturing. Accurate predictions can significantly impact decision-making processes. However, the scarcity of real-world data often hampers the performance of machine learning models. Data augmentation, which involves generating synthetic data to expand the training dataset, is a common solution. Traditional augmentation methods, however, often fail to maintain the temporal coherence necessary for TSF. This study introduces two novel augmentation techniques, Wavelet Masking (WaveMask) and Wavelet Mixing (WaveMix), leveraging the discrete wavelet transform (DWT) to preserve temporal dependencies while adjusting frequency elements in time series data.
Related Work
Basic Augmentation Methods
Basic augmentation techniques such as scaling, flipping, window cropping, Gaussian noise injection, and dynamic time warping are commonly used in time series analysis. However, these methods often disrupt the temporal coherence of the data, making them unsuitable for TSF.
Decomposition-Based Augmentation Methods
Decomposition-based approaches, like RobustSTL and STL, break down time series data into trend, seasonality, and residual components. These components are then transformed and recombined to generate new data. The STAug method, which uses Empirical Mode Decomposition (EMD), is one such approach but is memory-intensive and inefficient for large datasets.
Frequency-Domain Augmentation Methods
Frequency-domain methods, such as FrAug, manipulate frequency components using the Fourier transform. While effective, these methods focus solely on frequency components, neglecting time resolution. The wavelet transform, with its variable window sizes, offers a more balanced approach by providing high frequency resolution for small frequency values and low time resolution for large frequency values.
Research Methodology
Problem Formulation
The study focuses on multivariate time series forecasting. Given a time series sequence (X = (x_1, …, x_T) \in \mathbb{R}^{T \times K}), the goal is to forecast future values based on observed data up to timestamp (t < T). The objective is to learn a model (f) that forecasts future values (F = (x_{t+1}, …, x_T) \in \mathbb{R}^{(T-t) \times K}).
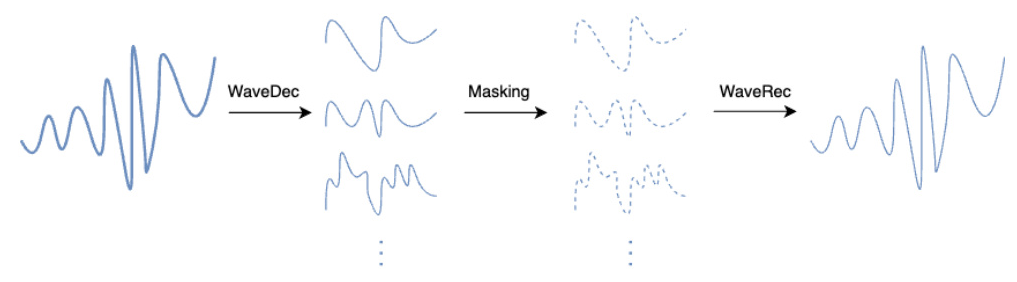
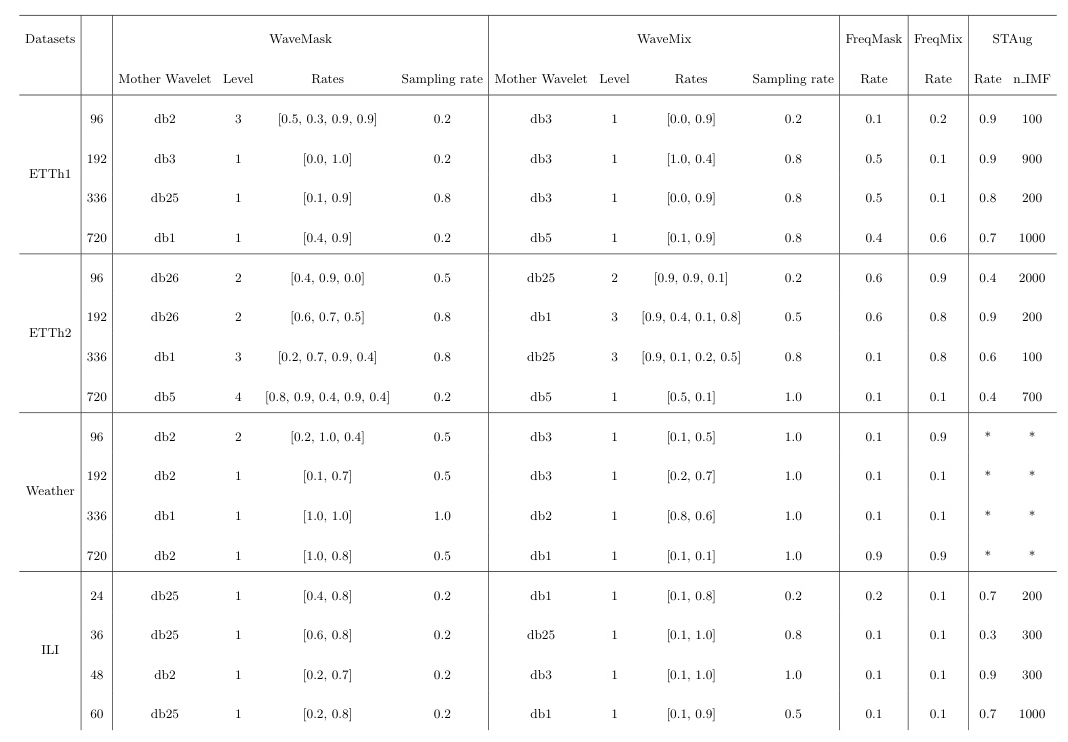
Wavelet Masking (WaveMask)
WaveMask creates synthetic data by selectively eliminating specific wavelet coefficients at each decomposition level, introducing variability in the augmented data. The process involves:
1. Concatenating the look-back window and target horizon.
2. Performing multilevel DWT to decompose the signal.
3. Masking wavelet coefficients based on predefined rates.
4. Reconstructing the signal using the inverse DWT.
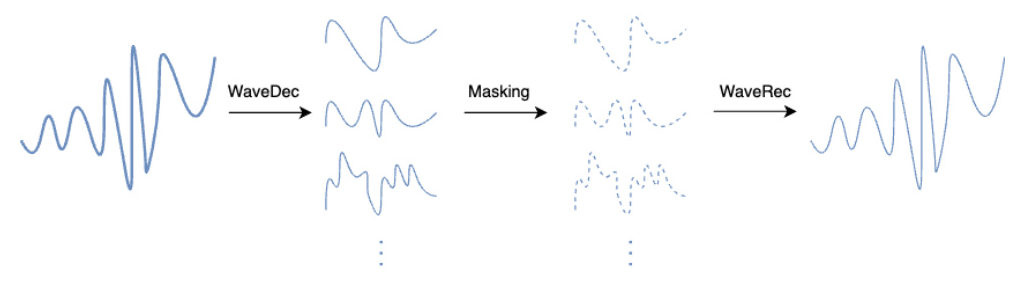
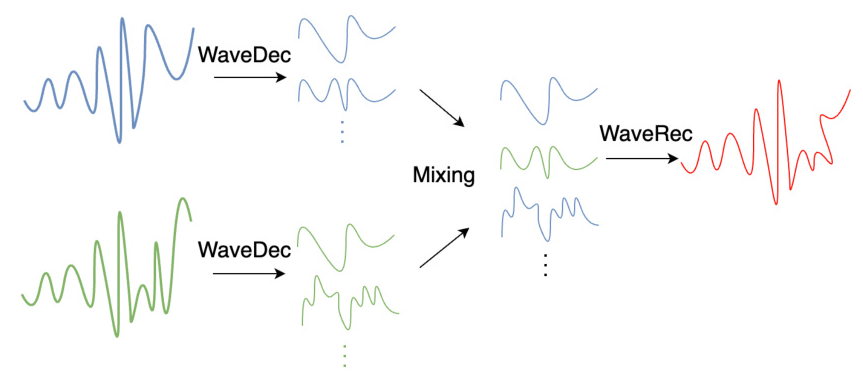
Wavelet Mixing (WaveMix)
WaveMix extends WaveMask by mixing wavelet coefficients from two different input signals. The process involves:
1. Concatenating look-back windows with corresponding target horizons for two input pairs.
2. Performing multilevel DWT for both input pairs.
3. Generating binary masks to select coefficients from each input signal.
4. Reconstructing the signal using the mixed coefficients.
Experimental Design
Datasets, Baselines, and Experimental Setup
The methods were evaluated using four datasets: ETTh1, ETTh2, Weather, and ILI. The datasets represent diverse TSF tasks across different domains. The experiments used a 24-length look-back window and forecasting horizons of 24, 36, 48, and 60 for ILI, and a 336-length look-back window with forecasting horizons of 96, 192, 336, and 720 for the other datasets. The datasets were split into train, validation, and test sets in a 6:2:2 ratio.
Evaluation Metrics
The performance was evaluated using Mean Squared Error (MSE) and Mean Absolute Error (MAE). The DLinear model was used, and parameters were fine-tuned through Random Search, while baseline methods employed Grid Search.

Results and Analysis
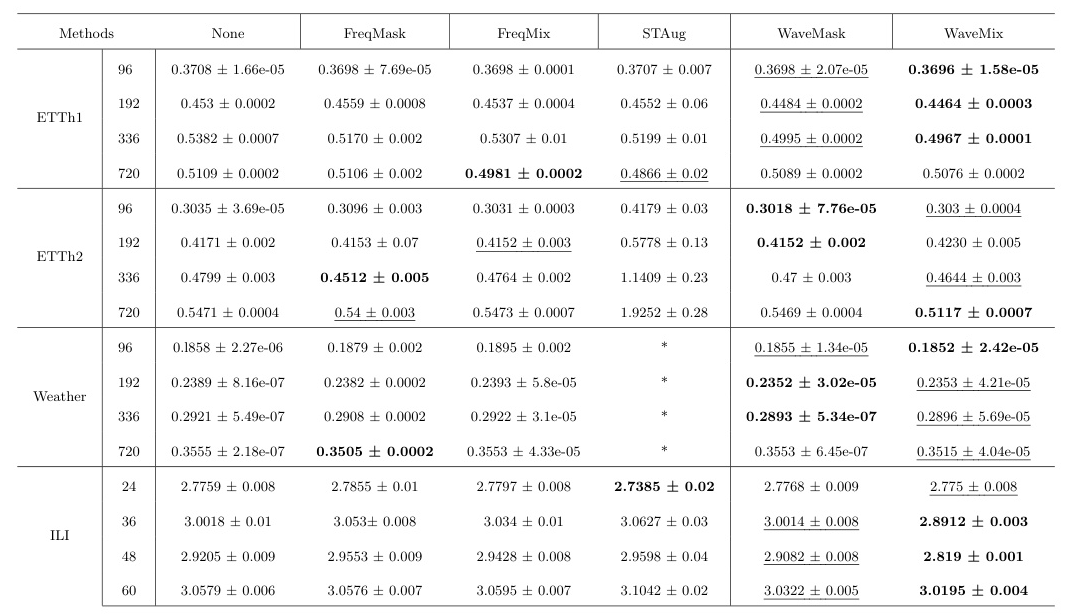
Main Results
WaveMask and WaveMix outperformed baseline methods in 12 out of 16 forecasting tasks. The methods demonstrated superior performance in terms of MSE and MAE, particularly in the ETTh1, ETTh2, and Weather datasets. The STAug method faced memory issues with the Weather dataset, highlighting its inefficiency for large datasets.
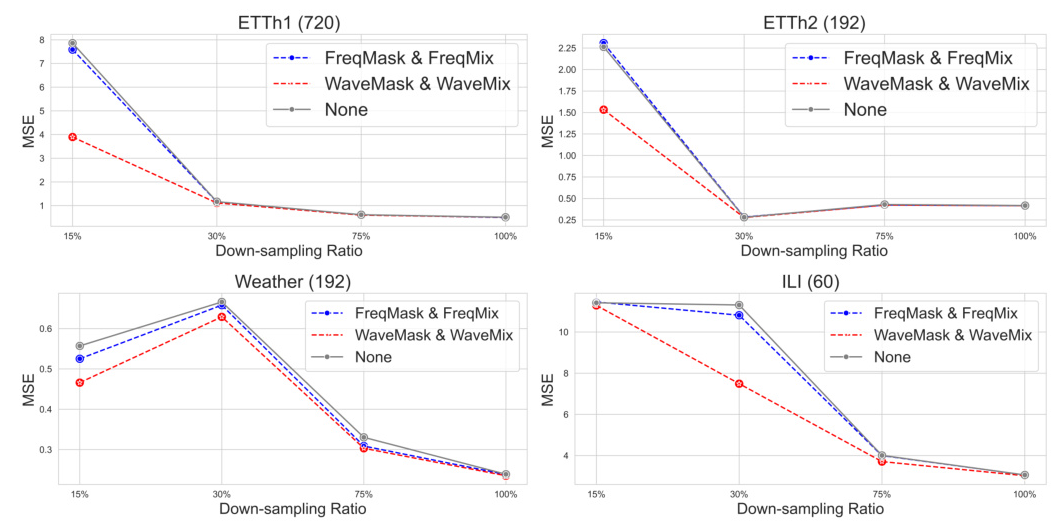
Ablation Study
The ablation study evaluated cold-start forecasting using downsampled training datasets. WaveMask and WaveMix consistently delivered superior results, especially at lower downsampling rates (15%). The study suggests that hyperparameter optimization could further enhance the performance of these methods.
Overall Conclusion
WaveMask and WaveMix are effective and straightforward augmentation techniques for TSF, outperforming traditional methods that focus solely on the frequency domain. These methods maintain temporal coherence while introducing variability, making them suitable for diverse TSF tasks. Future research could explore more sophisticated search techniques for hyperparameter optimization and the application of these methods to other models like TSMixer.
In conclusion, WaveMask and WaveMix offer promising solutions for enhancing TSF models, particularly in scenarios with limited real-world data. Their ability to preserve temporal dependencies while adjusting frequency elements sets them apart from traditional augmentation methods.
Code:
https://github.com/jafarbakhshaliyev/wave-augs