Authors:
Subrat Prasad Panda、Blaise Genest、Arvind Easwaran、Ponnuthurai Nagaratnam Suganthan
Paper:
https://arxiv.org/abs/2408.09135
Vanilla Gradient Descent for Oblique Decision Trees: A Detailed Exploration
Introduction
Decision Trees (DTs) are a cornerstone of machine learning, particularly valued for their performance on tabular data. Despite their popularity, learning accurate DTs, especially oblique DTs, is a complex and time-consuming task. Traditional DTs often suffer from overfitting and poor generalization in regression tasks. Recent advancements have aimed to make DTs differentiable, enabling the use of gradient descent algorithms for training. This paper introduces DTSemNet, a novel architecture that encodes oblique DTs as Neural Networks (NNs), allowing for efficient training using standard vanilla gradient descent.
Related Work
Non-Gradient-Based DT Training
Traditional methods for training DTs include:
– Greedy Optimization: Techniques like Classification and Regression Trees (CART) grow trees using split criteria.
– Non-Greedy Optimization: Methods like Tree Alternating Optimization (TAO) optimize decision nodes under a global objective.
– Global Searches: Approaches like Mixed Integer Programs (MIP) and Evolutionary Algorithms (EA) search over various DT structures.
– Gradient Descent: Recent methods make DTs differentiable, allowing gradient descent for training.
Gradient-Based DT Training
Most gradient-based approaches approximate DTs as soft-DTs using functions like Sigmoid, which results in probabilistic decisions. Hard DTs can be derived from soft DTs but often at the cost of accuracy. Methods like Dense Gradient Trees (DGT) and Interpretable Continuous Control Trees (ICCT) use approximations during backpropagation, which can hinder training efficiency.
Research Methodology
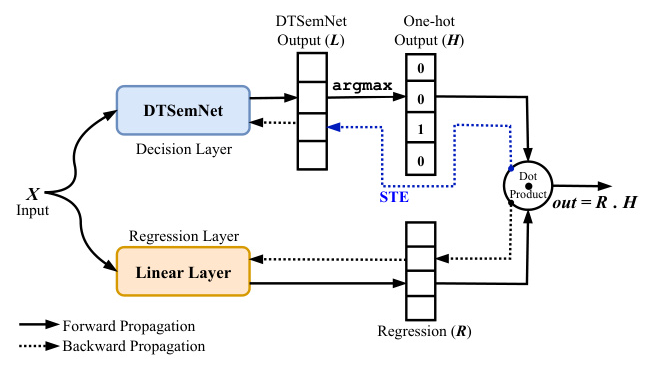
DTSemNet Architecture
DTSemNet encodes oblique DTs as NNs using ReLU activation functions and linear operations, making it fully differentiable. The architecture ensures that the decisions in the DT correspond one-to-one with the trainable weights in the NN. This encoding allows for efficient training using standard gradient descent without the need for approximations.
Key Features:
- Input Layer: Consists of inputs for the feature space and a bias term.
- First Hidden Layer: Contains nodes corresponding to the internal nodes of the DT, with linear activation functions.
- Second Hidden Layer: Includes nodes representing true or false decisions, with ReLU activation functions.
- Output Layer: Comprises nodes corresponding to the leaves of the DT, with linear activation functions.
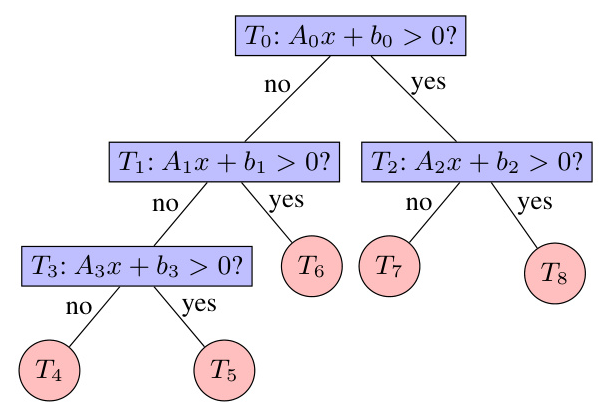
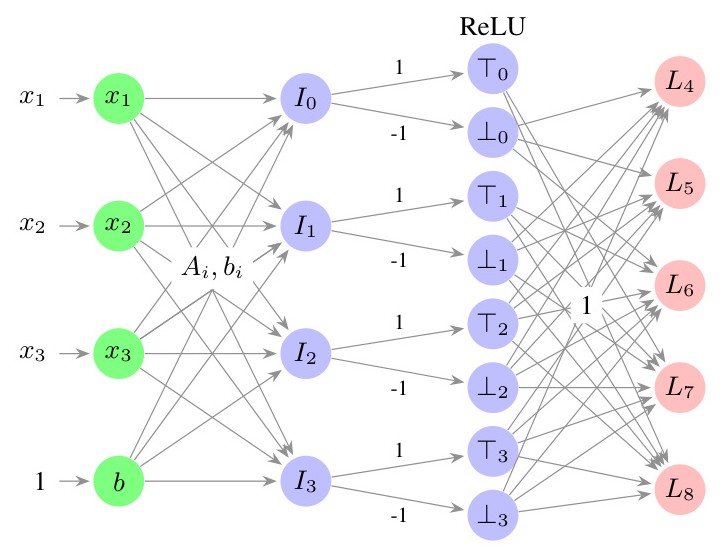
Theorem 1: Semantic Equivalence
Theorem 1 proves that DTSemNet is semantically equivalent to a DT. For any input, the output class produced by DTSemNet is the same as that produced by the DT.
Experimental Design
Classification Tasks
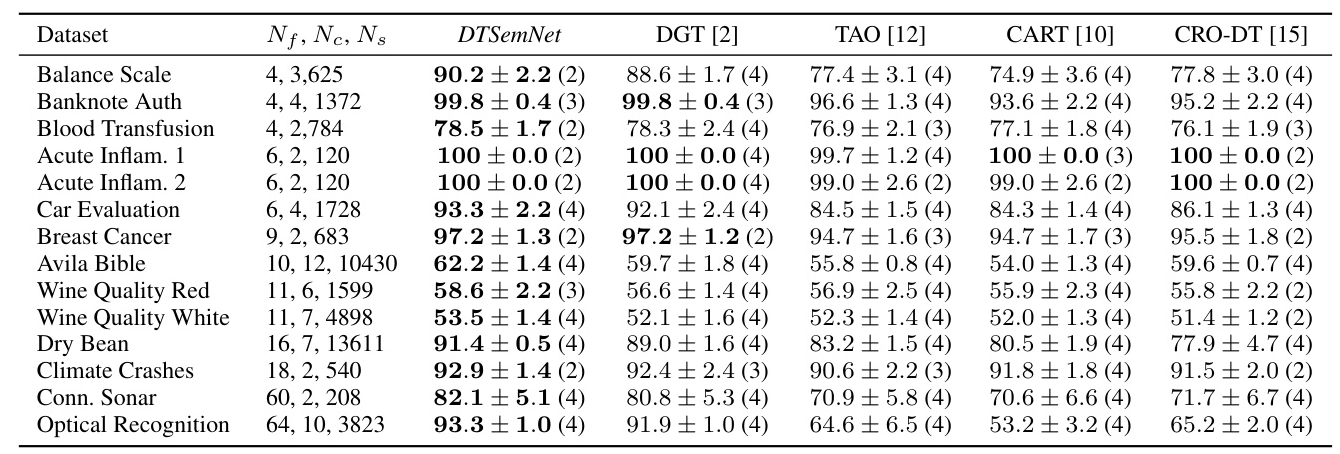
The experiments involve various classification benchmarks, comparing DTSemNet with state-of-the-art methods like DGT, TAO, CRO-DT, and CART. The datasets include tabular data and a small-sized image dataset (MNIST).
Regression Tasks
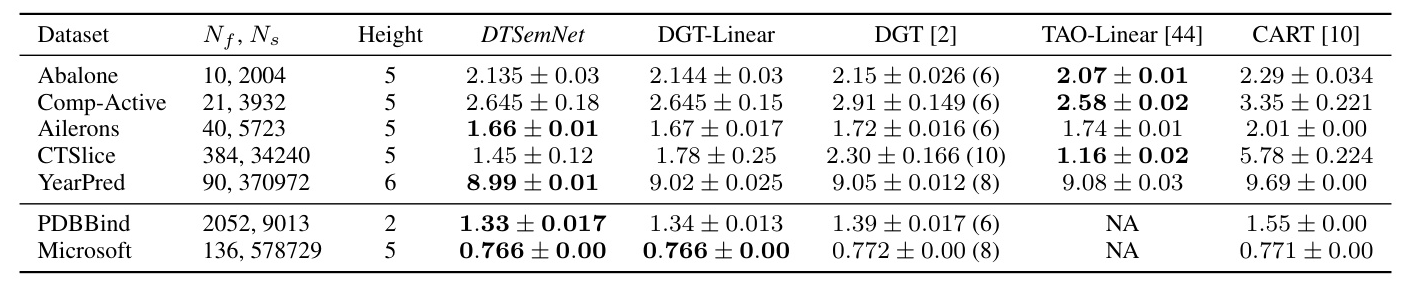
For regression tasks, DTSemNet is extended to include a regression layer at the leaves. The performance is compared with DGT, TAO-linear, and CART on several regression benchmarks.
Reinforcement Learning (RL) Tasks
DTSemNet is also evaluated in RL environments with both discrete and continuous action spaces. The architecture is integrated into RL pipelines like PPO, and its performance is compared with NN policies and other DT-based methods.
Results and Analysis
Classification Performance
DTSemNet consistently outperforms other methods in classification tasks, achieving the highest accuracy across all datasets. The architecture’s efficiency is particularly evident in benchmarks with a larger number of features.
Regression Performance
In regression tasks, DTSemNet-regression performs competitively, often achieving the best or second-best results. The use of a single STE approximation for regression tasks helps maintain high efficiency.
RL Performance
In RL tasks, DTSemNet matches or exceeds the performance of NN policies, especially in environments with a limited number of features. The architecture’s ability to handle oblique trees makes it more expressive and accurate than axis-aligned DTs.

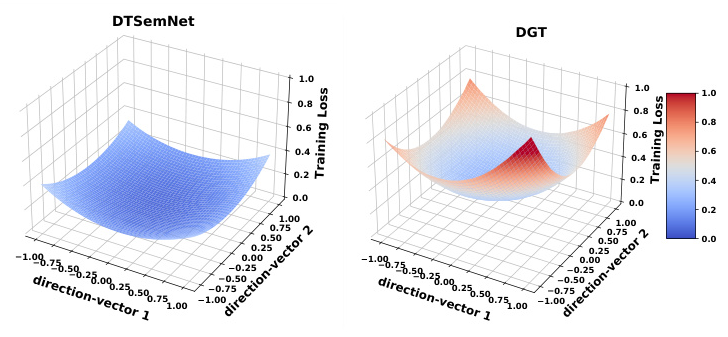
Loss Landscape Analysis
The loss landscape analysis shows that DTSemNet has a flatter loss landscape compared to DGT, indicating better generalization capabilities.
Overall Conclusion
DTSemNet introduces a novel way to encode oblique DTs as NNs, enabling efficient training using vanilla gradient descent. The architecture proves to be more accurate and faster than competing methods in both classification and regression tasks. In RL environments, DTSemNet generates highly efficient DT policies, outperforming other DT-based methods.
Limitations and Future Work
While DTSemNet excels in tasks with limited features, it is less suitable for high-dimensional inputs like images. Future work will focus on developing a regression architecture without STE approximations and introducing differentiable methods for tree pruning and adaptive growth.
This detailed exploration of DTSemNet highlights its innovative approach to training oblique DTs using gradient descent, offering significant improvements in accuracy and efficiency across various benchmarks. The architecture’s versatility in both supervised learning and RL tasks makes it a valuable contribution to the field of machine learning.