Authors:
Björn Schembera、Frank Wübbeling、Hendrik Kleikamp、Burkhard Schmidt、Aurela Shehu、Marco Reidelbach、Christine Biedinger、Jochen Fiedler、Thomas Koprucki、Dorothea Iglezakis、Dominik Göddeke
Paper:
https://arxiv.org/abs/2408.10003
Introduction
In the realm of scientific research, data and knowledge-driven approaches have emerged as the fourth pillar of science. The proliferation of computer simulations, big measurement data in physics, and statistical data in social sciences underscores the importance of processing and generating data for scientific reasoning. Sharing and citing research data is increasingly recognized as a crucial aspect of the scientific process, necessitating adherence to the FAIR principles (Findable, Accessible, Interoperable, Reusable) to avoid dark data and ensure reproducibility.
In fields utilizing mathematical methods, research data manifests in various forms, extending beyond classical mathematical artifacts like proofs and formulae to include vast amounts of data generated through numerical methods. To achieve a comprehensive epistemic understanding, it is imperative to document all models and solution algorithms. This documentation not only facilitates reproducibility but also aids in identifying alternate, competing, or complementary models and solution schemes.
Building on the conceptual foundations for semantic knowledge representation of mathematical models and algorithms, this paper presents a matured version of a joint ontology and a knowledge graph (KG) with over 2000 elements, ready for production service.
Related Work
The development and use of ontologies in mathematics are still in their nascent stages. Preliminary work includes taxonomic classifications of mathematical artifacts and educational approaches. However, these ontologies primarily focus on educational and taxonomic purposes and do not encompass many mathematical objects relevant to our work.
Subject-specific ontologies exist for mathematical models in domains like plasma physics, biology, and neural networks. Our approach aims to create a general, modular ontology for mathematical models and numerical algorithms, capable of connecting with other ontologies and knowledge frameworks in the context of Linked Open Data.
The Algorithms Metadata Vocabulary and the MEX Algorithm Ontology provide detailed knowledge about algorithms from a computer science perspective. However, our focus is solely on mathematical algorithms. The work is driven by the Mathematical Research Data Initiative (MaRDI) within the National German Research Data Infrastructure (NFDI), aiming to build a linked data infrastructure and semantic technology.
Research Methodology
Merging MathModDB and MathAlgoDB
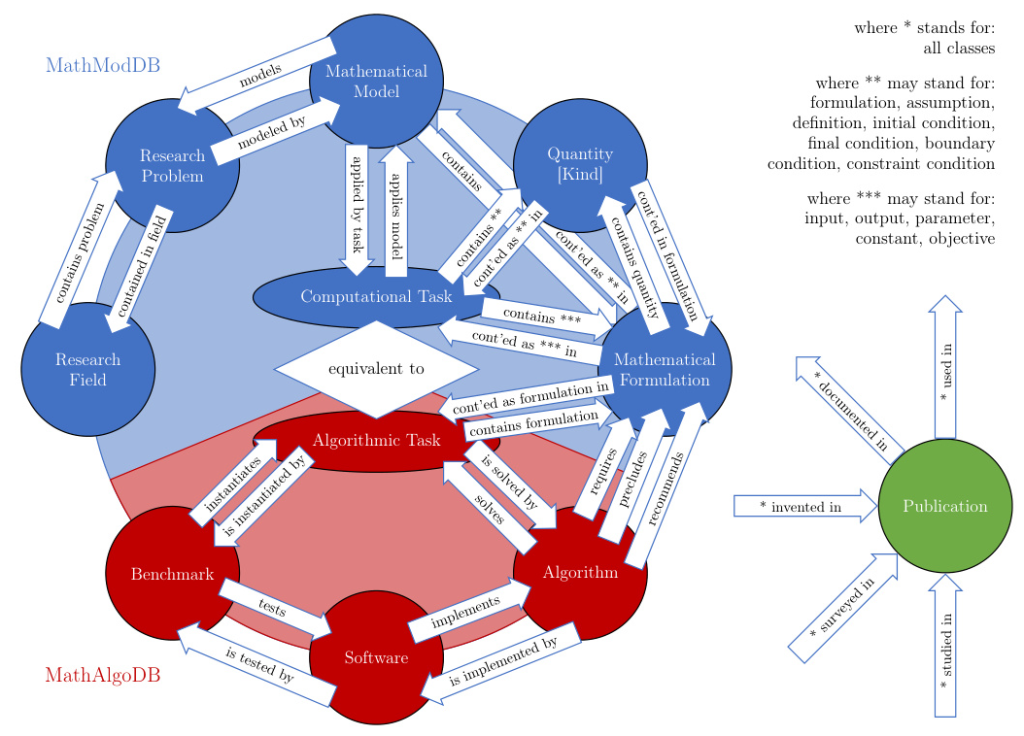
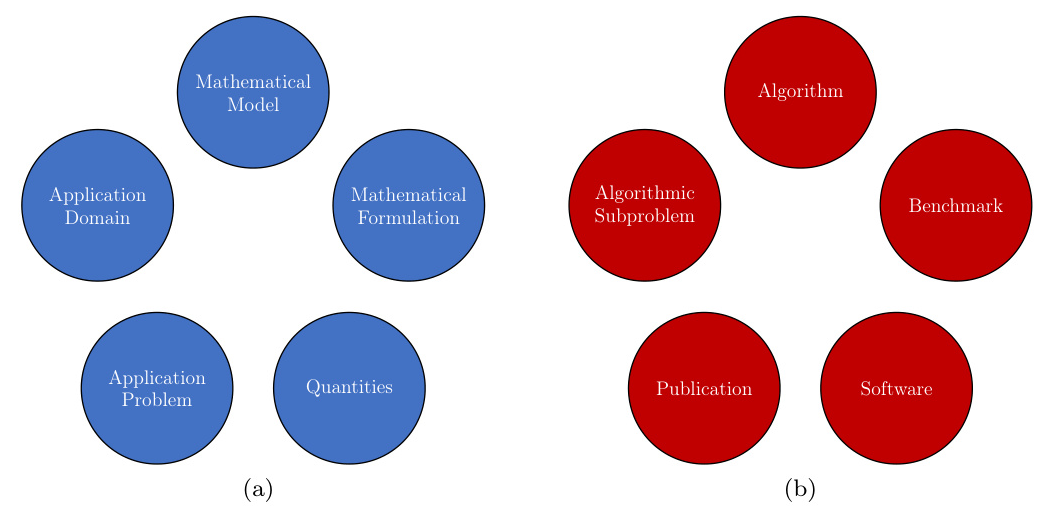
The previously introduced ontologies for mathematical models (MathModDB) and algorithms (MathAlgoDB) were reviewed and extended. The essential classes of these ontologies are depicted in Figure 1.
Previous Ontology Structures and Their Shortcomings
The original ontologies had inconsistencies with standard nomenclature and required major adjustments. The connection between mathematical modeling and algorithmic subproblems was challenging, necessitating the addition of mathematical problems to MathAlgoDB as Algorithmic Problems.
Computational Tasks as the Missing Link
To unify the two ontologies, a Computational Task class was introduced, representing the semantic information content closely related to an algorithmic problem class. This class bridges the gap between mathematical models and algorithms.
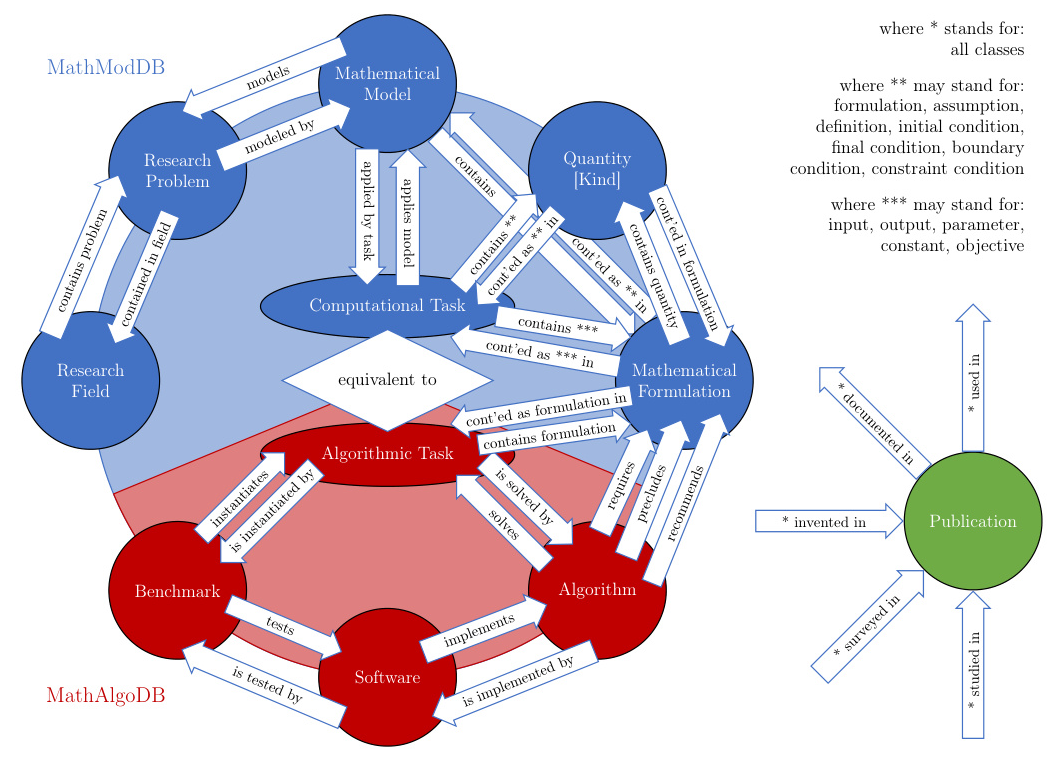
Quantities in Semantic Knowledge Representation
Quantities play a crucial role in mathematical expressions, giving models their semantic meaning. The Quantity Kind class was introduced to distinguish basic quantities from specific use case quantities, enhancing clarity and precision.
Metadata Enrichment for Mathematical Models and Algorithms
The ontologies were revised to integrate external information sources and controlled vocabularies, driving the enrichment of the KG with metadata. This includes linking individuals to identifiers from QUDT, DFG, MSC, and PhySH classification systems. Subject-specific metadata, such as natural language descriptions and mathematical expressions in LaTeX or MathML, can also be integrated.
Experimental Design
Living Knowledge Graph of Models & Algorithms
As of mid-August 2024, over 120 mathematical models and 200 algorithms have been added to the KG, covering various research fields. The data corpus consists of manually maintained, curated information to ensure high data quality.
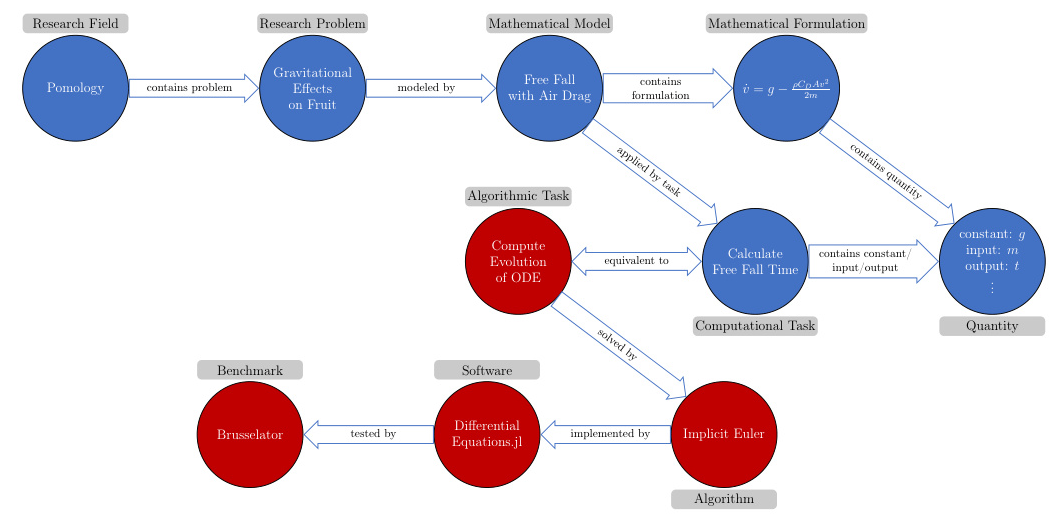
Use Case: From Falling Apples to Moving Planets
An illustrative example is the story of Sir Isaac Newton formulating his theory of gravitation by observing a falling apple. This example is implemented in the MathModDB KG, including models for free fall with and without air drag. The corresponding computational tasks and suitable numerical solvers for ordinary differential equations are also included.
Use Case: Romanization of Northern Tunisia
Another example is the study of Romanization spreading in Northern Tunisia using a susceptible-infected (SI) model. The model describes the change in the number of susceptible and infected cities over time, with computational tasks for determining spreading curves and optimal parameters.
Data Flows in the Knowledge Graph
Templates were developed to facilitate the process for researchers to add mathematical models to the MathModDB, ensuring the models are FAIR. The MathAlgoDB KG can be accessed via a web interface for retrieving information and adding new data.
Results and Analysis
The joint ontology and KG have successfully integrated over 250 models and algorithms, primarily from applied and numerical mathematics. The examples demonstrate the ontology’s capability to semantically represent essential parts of modeling and simulation. The SPARQL query provided in the paper can be used to find applicable algorithms for specific research problems.

Overall Conclusion
The paper presents extensions and a conceptual redesign of ontologies for mathematical models and algorithms, resulting in a living knowledge graph. The extensions include harmonization efforts, the introduction of a Computational Task class, incorporation of controlled vocabularies, and metadata enrichment for both models and algorithms. The KG now semantically represents essential parts of modeling and simulation in various mathematized branches of science.
Future work will focus on adapting the joint ontology to other areas of mathematics, addressing limitations like the handling of discretization, and developing strategies for partially automating the data ingestion process. The KG will be incorporated into the MaRDI portal, enabling the assignment of persistent IDs for models and algorithms.
This blog post provides a detailed overview of the paper “Towards a Knowledge Graph for Models and Algorithms in Applied Mathematics,” highlighting the background, related work, research methodology, experimental design, results, and overall conclusion. The illustrations from the paper are included to enhance understanding.