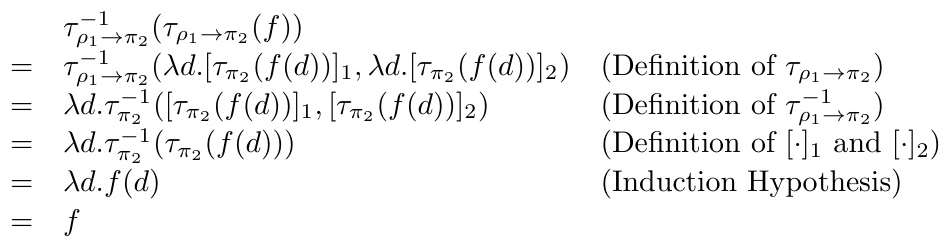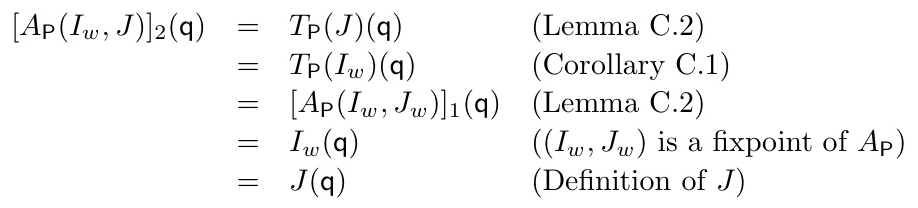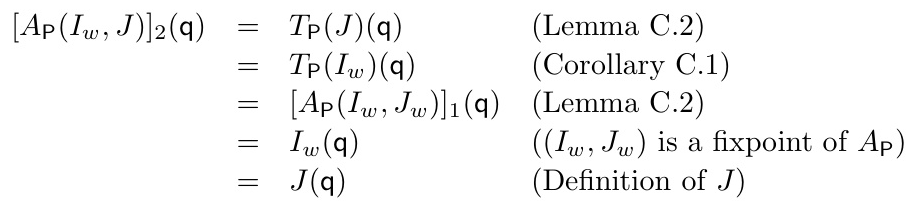Authors:
Bart Bogaerts、Angelos Charalambidis、Giannos Chatziagapis、Babis Kostopoulos、Samuele Pollaci、Panos Rondogiannis
Paper:
https://arxiv.org/abs/2408.10563
Introduction
Higher-order logic programming languages have been shown to possess powerful expressive capabilities and elegant semantic properties. These languages extend classical first-order logic programming, allowing for more complex abstractions and manipulations. However, defining a stable model semantics for higher-order logic programs that generalizes the seminal work of Gelfond and Lifschitz (1988) has been a challenging task. This paper proposes a stable model semantics for higher-order logic programs using Approximation Fixpoint Theory (AFT), a formalism that has successfully unified semantics across various non-monotonic formalisms.
Related Work
Extensions of Logic Programming
Several extensions of standard logic programming have been proposed to enhance its expressive power. For instance, logic programming with aggregates and higher-order logic programs have been studied using AFT. Previous works have also explored the well-founded semantics for higher-order logic programs and the stable-unstable semantics for second-order quantification over answer sets.
Approximation Fixpoint Theory (AFT)
AFT has been applied to various fields, including abstract argumentation, active integrity constraints, stream reasoning, and constraint languages for the semantic web. It provides a lattice-theoretic framework to define new semantics and study their properties without reinventing the wheel.
Research Methodology
Higher-Order Logic Programming Language (HOL)
The proposed language, HOL, is based on a simple type system with two base types: o (Boolean domain) and ι (domain of data objects). Composite types are partitioned into predicate and argument types. The syntax of HOL includes predicate variables, predicate constants, individual variables, individual constants, and various logical operators.
Immediate Consequence Operator
The immediate consequence operator for HOL programs generalizes the classical TP operator for first-order logic programs. It evaluates the bodies of rules and defines the semantics of expressions and bodies in a two-valued setting.
Experimental Design
Motivating Example: Max-Clique Problem
The max-clique problem is used to illustrate the higher-order logic programming language. The problem is defined using predicates to represent vertices and edges of a graph, and higher-order predicates to define cliques and maximal cliques. The solution demonstrates the power of abstraction and reuse in higher-order logic programming.
“`prolog
% Pick a set of vertices (emulate choice rule)
pick X ← v X, ∼(npick X).
npick X ← v X, ∼(pick X).
% Define what it means for a set of vertices to be a clique
hasNonEdge P ← P X, P Y, ∼(X ≈ Y), ∼(e X Y).
clique P ← subset P v, ∼(hasNonEdge P).
% Define what it means to be a max-clique:
maxclique P ← maximal subset clique P.
% The selected set should be a max-clique
f ← ∼f, ∼(maxclique pick).
“`
Syntax and Semantics of HOL
The syntax of HOL includes rules and programs, with rules consisting of a head and a body. The semantics of HOL is defined using Herbrand interpretations and states, with a partial order on the elements of each type.
Results and Analysis
Two-Valued and Three-Valued Semantics
The two-valued semantics of HOL is extended to a three-valued setting to handle circularities through negation. Three-valued relations are defined at all orders of the type hierarchy, and the semantics of expressions and bodies are evaluated in this three-valued truth space.
Approximation Fixpoint Theory (AFT)
AFT is used to define the stable model semantics for higher-order logic programs. The immediate consequence operator is approximated with a ⪯-monotone function, and various semantics (supported model, Kripke-Kleene, well-founded) are derived from this approximation.
Properties of the Stable Model Semantics
The proposed stable model semantics generalizes classical stable models and preserves their desirable properties, such as minimality and uniqueness for stratified programs. The semantics is shown to be an extension of classical stable models and three-valued stable models.
Overall Conclusion
The proposed stable model semantics for higher-order logic programs provides a powerful and versatile formalism that generalizes classical stable models. Using Approximation Fixpoint Theory, the semantics retains desirable properties and offers alternative semantics for higher-order logic programs. The examples and properties discussed in the paper demonstrate the potential of higher-order logic programming under the stable model semantics to form the basis of novel Answer Set Programming (ASP) systems.