Authors:Manuel R. Torres、Parisa Zehtab、Michael Cashmore、Daniele Magazzeni、Manuela Veloso
ArXiv:https://arxiv.org/abs/2408.13208
Introduction
Background
One of the most amazing implementations of AI in so many areas such as scheduling, resources allocation, robotics and autonomous vehicles is automated decision-making. Traditionally, these decision-making processes are designed to maximize an overall benefit (or minimize a cost). But as AI systems are more and more embedded into society, it becomes essential to ensure that those system function correctly.
Problem Statement
While decision-making fairness is a well-studied area, existing approaches mostly consider static one-time decisions. In this paper, we take a new perspective and develop the notion of temporal fairness to account for fairness in time. This approach is powerful because it can remedy historical unfairness and leverage future predictions in order to produce fairer outcomes over long timescales.
Related Work
Existing Fairness Formulations
AI fairness has been studied under different fields such as robotics, healthcare, telecommunications and resource allocation. Common formulations of fairness explicitly enforce that outcomes are made equal over time. Nonetheless, these approaches may not consider a history of injustices from previous decisions.
Long-term Fairness
Fairness over longer time scales (in particular, in the contexts of machine learning and sequential decision-making) has started to receive research attention recently. These papers all have something to say about the effect of a history of decisions; that is, an abundant series approach offers fairness over time.
Fairness in Scheduling and Resource Allocation
In real-time systems, fairness in scheduling and resource allocation has been studied extensively. Such studies are generally designed to ensure a just distribution of tasks or resources and often do not account for past inequities.
Research Methodology
Optimization Problem (OP)
The problem formulation starts with a general optimization problem (OP) of maximizing some quality metric Q subject to constraints C. This formulation does not incorporate fairness, which could lead to arbitrary solutions.
Fair Optimization Problem (FOP)
After using fairness in Prune the Trade-off Problem (PTP) for balanced pruning to a desirable solution quality and model peak capacity, Fair Optimization Problem (FOP) identifies different fairness measure function already existed that specializes on how they generate their core similarities. We seek to identify the solution whose quality (Q )is maximized, as well its fairness indicator (F).
Historical Fair Optimization Problem (HFOP)
HFOP extends FOP by incorporating a historical fairness measure (F_H) that takes into account the fairness of past solutions. This approach aims to account for historically accumulated unfairness.
Discounted Historical Fair Optimization Problem (DHFOP)
DHFOP introduces a discount factor (\gamma) to the historical fairness measure, allowing more recent decisions to have a greater impact on the fairness assessment. This approach models the “forgetting rate phenomenon” where recent events are considered more important than events in the distant past.
Multi-Step Discounted Historical Fair Optimization Problem (MSDHFOP)
MSDHFOP further extends DHFOP by incorporating future predictions. This approach allows planning over multiple time steps while accounting for historical unfairness and future constraints.
Experimental Design
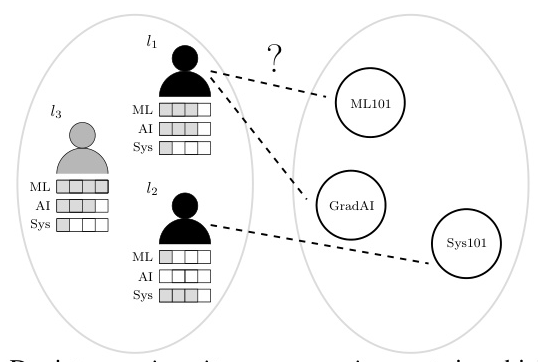
Course Assignment Problem (CAP)
CAP consists of assigning lecturers to their courses based on their expertise. Quality metrics reward assignments with skilled lecturers, while various fairness metrics are used to assess the fairness of assignments.
Vehicle Routing Problem (VRP)
In the VRP, vehicles must travel to a set of points while minimizing the total distance traveled. The fairness metric ensures a balanced distribution of travel distances among the vehicles.
Task Allocation Problem (TAP)
TAP consists of assigning tasks to agents to minimize the total cost. Fairness metrics ensure that the cost is evenly distributed among agents.
Nurse Scheduling Problem (NSP)
NSP involves scheduling nurse shifts while taking into account historical unfairness and future constraints. The impact of different historical and discounting factors is evaluated.
Results and Analysis
Quality vs. Fairness Trade-off
The study evaluates the trade-off between quality and fairness by varying the parameter (\beta). Higher values of (\beta) result in lower solution quality but higher fairness and historical fairness.
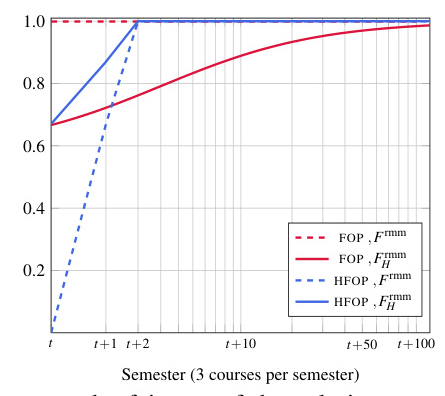
Planning with Future Forecasts
The advantages of MSDHFOP are demonstrated by comparing it with HFOP. MSDHFOP can exploit future constraints, thereby improving overall quality and fairness.
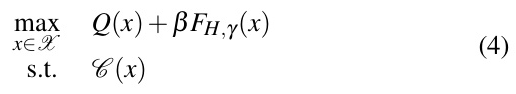
Increasing Complexity and Benchmarking
The study evaluates the impact of fairness on runtime. Although FOP and HFOP require more computational time than OP, the increase is not prohibitive.
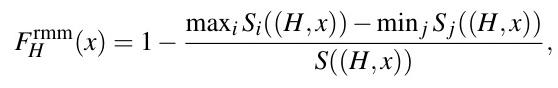
Larger Scale Experimentation
The framework is applied to a larger TAP instance, demonstrating its scalability and effectiveness in ensuring fairness.
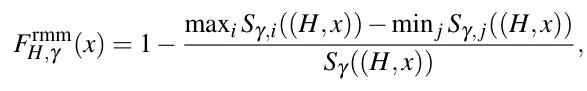
Overall Conclusion
Summary
This study introduces the concept of temporal fairness in the decision-making process, addresses historical unfairness and incorporates future predictions. The proposed formulations—FOP, HFOP, DHFOP, and MSDHFOP—provide a comprehensive framework to ensure fair results over time.
Future Work
Future research can explore scenarios with different temporal fairness metrics, as well as the use of multiple concurrent fairness metrics. In addition, further research is needed on the application of temporal fairness in other fields and real-world situations.
Disclaimer
This research was conducted by the JPMorgan Chase AI Research Group and does not constitute investment advice or recommendations for any financial products or services.
By incorporating temporal fairness into the decision-making process, this research takes an important step towards more ethical and fair AI systems. The proposed approach provides a powerful framework for addressing historical injustices and planning for fairer future outcomes.
