Authors:
Paper:
https://arxiv.org/abs/2408.08550
String Diagram of Optimal Transports: A Detailed Interpretive Blog
Introduction
Optimal transport (OT) is a classical problem in operations research, initially formulated by Kantrovich in 1942. It involves computing the minimum transportation cost between two discrete distributions. This problem has applications in various fields, including artificial intelligence and hierarchical reinforcement learning. In real-world scenarios, models often have hierarchical structures, such as buildings consisting of rooms or maps consisting of streets. String diagrams, a graphical language, can naturally capture these hierarchical structures using two algebraic compositions: sequential composition (#) and parallel composition (⊗).
In this paper, the authors propose a hierarchical framework for optimal transports (OTs) using string diagrams. They address a safety problem that requires proving or disproving that the minimum transportation cost in a given string diagram of OTs is above a specified threshold. By reducing the safety problem on a string diagram of OTs to a monolithic OT, the authors introduce a novel algorithm that demonstrates efficiency and performance advantages through experiments.
Overview
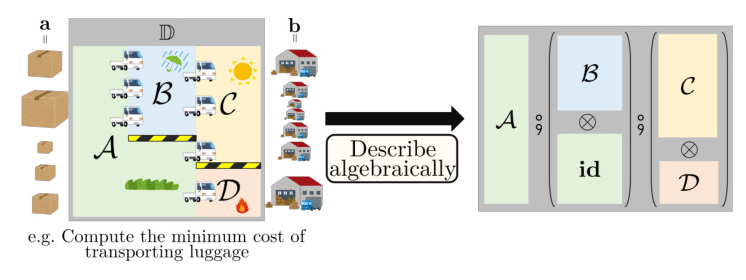
The paper begins with an overview of the target problem and the proposed approach. The setting involves four connected regions (A, B, C, D) with interfaces denoted by arrows. The goal is to compute the minimum transportation cost from a given distribution to a specified destination. The target problem is to prove or disprove that the minimum transportation cost is not less than a given threshold λ.
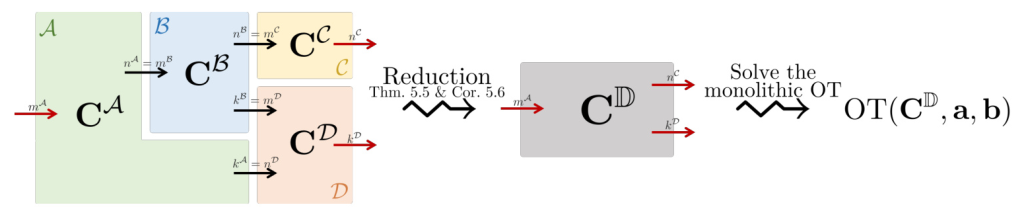
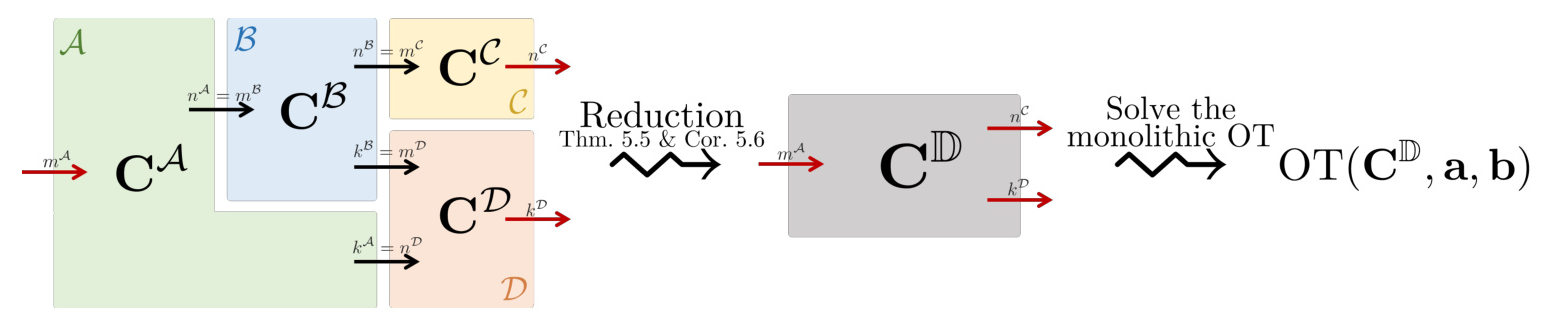
The approach involves describing the diagram as compositions of components, called string diagrams of OTs. The authors introduce a novel reduction from a string diagram of OTs to a monolithic OT, leveraging the algebraic structure of cost matrices. This reduction allows the use of existing algorithms for OTs to solve the safety problem efficiently.
Compositions of Optimal Transports
The authors introduce two compositions of OTs: sequential composition (#) and parallel composition (⊗).
Sequentially Composed OT
Given two open OTs (oOTs) A and B, and two distributions a and b, the sequentially composed OT is defined by minimizing the transportation cost while satisfying consistency conditions with the distributions and connections.
Parallelly Composed OT
Given two oOTs A and B, and two distributions a and b, the parallelly composed OT is defined by minimizing the transportation cost independently for each oOT, with consistency conditions for the distributions.
Duality
The dual problems of sequentially and parallelly composed OTs reveal an algebraic structure in OTs.
Dual Problem of Sequentially Composed OTs
The dual problem of a sequentially composed OT involves maximizing a function subject to constraints that are equivalent to the dual problem of the OT with a composed cost matrix.
Dual Problem of Parallelly Composed OT
The dual problem of a parallelly composed OT involves maximizing a function subject to constraints that have a compositional interpretation. The parallel composition of cost matrices imposes penalties to prevent jumping between oOTs.
Aligned String Diagram of OTs
The authors introduce aligned string diagrams of OTs, a subclass of string diagrams of OTs. An aligned string diagram is a formula of oOTs with consistent compositions. The OT on an aligned string diagram is defined by minimizing the transportation cost subject to consistency conditions.
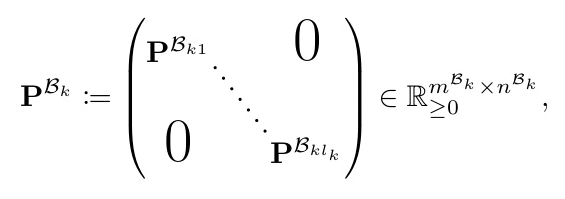
Dual Problem of Aligned String Diagram of OTs
The dual problem of an OT on an aligned string diagram involves maximizing a function subject to constraints defined by the composed cost matrix. The cost matrices form a symmetric strict monoidal category, allowing the definition of general string diagrams of OTs.
Algorithm
The authors present an algorithm for the safety problem on an aligned string diagram. The algorithm computes the minimum transportation cost by recursively composing cost matrices and solving the monolithic OT.
Beyond Aligned String Diagram
The authors extend the framework to general string diagrams of OTs, allowing more complex structures. They define the OT on string diagrams without assuming alignment and provide a reduction to sequential normal form.
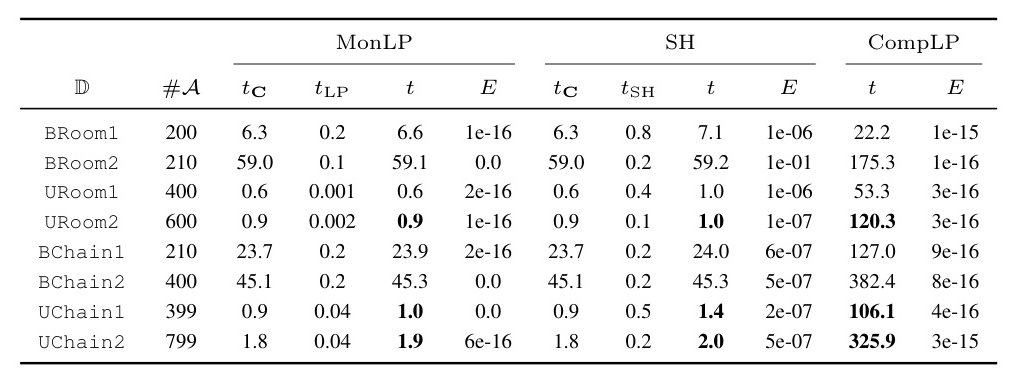
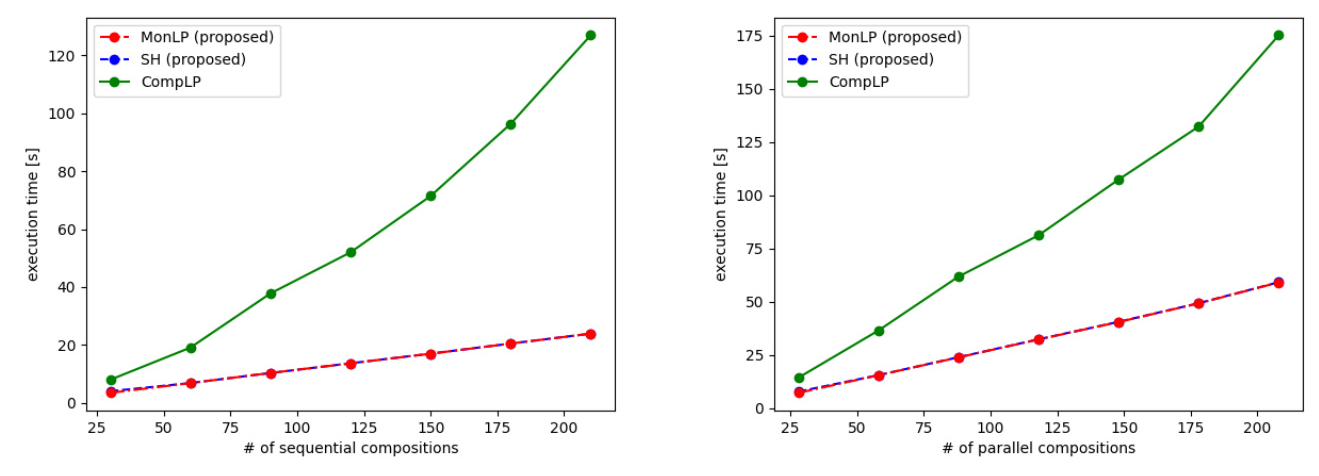
Experiments
The authors demonstrate the efficiency of their approach through experiments on four benchmarks: BRooms, URooms, BChains, and UChains. These benchmarks reflect common hierarchical structures found in real-world problems.
Discussion
The experiments show that the proposed monolithic approaches (MonLP and SH) outperform the naive LP approach (CompLP) in terms of speed and precision. The bottleneck is the computation of cost matrices, suggesting that efficient representations and computations for matrices over the min-tropical semiring could improve performance. The complexity of compositional structures affects the performance of the algorithms, with MonLP and SH showing clear advantages for more complex structures.
Related Work
The paper discusses related work in optimal transport with structures, string diagrams, and hierarchical reinforcement learning. The authors highlight the challenges in high-dimensional distributions and multi-marginal OT, and the use of hierarchical structures in reinforcement learning and verification of systems.
Conclusion
The authors introduce string diagrams as a hierarchical framework for OTs and provide a new algorithm that exploits the algebraic structure of cost matrices. The experiments demonstrate the algorithm’s performance advantages over naive linear programming. Future work includes developing hierarchical planning algorithms on string diagrams of OTs and extending the Sinkhorn algorithm to string diagrams of OTs.