Authors:
Clinton Enwerem、Erfaun Noorani、John S. Baras、Brian M. Sadler
Paper:
https://arxiv.org/abs/2408.08668
Introduction
In the realm of high-risk industries such as autonomous delivery and supply chain management, Stochastic Shortest-Path (SSP) problems are prevalent. These problems require robust planning algorithms to ensure successful task completion while mitigating hazardous outcomes. Traditional chance-constrained incremental sampling techniques for solving SSP problems tend to be overly conservative and often do not account for the likelihood of undesirable tail events. This paper introduces a risk-aware approach inspired by the Rapidly-Exploring Random Trees (RRT*) planning algorithm, which selects nodes along path segments with minimal Conditional Value-at-Risk (CVaR). This approach aims to optimize the path by considering the CVaR at each sampling iteration, leading to an optimal path in the limit of the sample size.
Background & Problem Formulation
Finding Shortest Paths in Planar Regions with Obstacles
The problem of finding shortest paths in a two-dimensional space with convex obstacles is defined. The configuration space (C-space) of the robot is represented by a non-empty compact set (X \subset \mathbb{R}^2), with its obstacle-free subset denoted as (X_{free}). The tree (T) representing (X_{free}) consists of nodes (V_T) and edges (E_T).
Path Definition
A path (p) is defined as a finite sequence of edges connecting the start node (x_{start}) to the goal node (x_{goal}), with each path segment lying entirely in (X_{free}). The length of each path segment is quantified by a non-negative real number (L_k).
SSP Problem
The SSP problem involves finding a path of minimum expected length that connects (x_{start}) and (x_{goal}), considering the uncertainty in path segment lengths. The problem is formally expressed as a mathematical program:
[
\begin{aligned}
& \min_{p \in P} \mathbb{E}[L] \
& \text{s.t.} \quad x_0 = x_{start}, \, x_N = x_{goal}, \, N \leq N_{max}, \
& \quad x_k \in X_{free}, \, L_k = \ell(p[k]), \, \forall k \in \mathbb{Z}{0,N{max}-1},
\end{aligned}
]
where (L) denotes the total path length, and the expectation is computed with respect to the underlying uncertainty distribution.
Uncertainty Quantification & Risk Notion
The inherent stochasticity in the SSP problem arises from various sources, such as localization inaccuracy and dynamic obstacles. The length of each path segment (L_k) is modeled as a Gaussian distribution with mean (c) and variance (\sigma^2_{C_k}). The risk at each stage is assessed using the (\alpha)-level CVaR, which quantifies the expected worst-case realization of (L_k).
Computing CVaR(_\alpha)((L_k))
The CVaR(\alpha) of a random variable (Y) is defined as the expected value of (Y) conditioned on (Y) being above the (\alpha)-quantile (VaR(\alpha)). For a normally distributed (L_k), the CVaR(_\alpha) is computed as:
[
\text{CVaR}\alpha(L_k) = \frac{1}{1 – \alpha} \int\alpha^1 (c + \varsigma(\alpha) \sigma_{C_k}) \, dL_k,
]
where (\varsigma(\alpha) = \sqrt{2} \, \text{erf}^{-1}(2\alpha – 1)).
Robust SSP Planning via Risk-Sensitive RRT*
SSP Planning with CVaR Criteria
The modified SSP problem aims to minimize the worst-case path length (L_{worst}), defined as the expected sum of the lengths of all path segments under the maximum noise variance. The problem is expressed as:
[
\begin{aligned}
& \min_{p \in P} J_{\text{CVaR}}(x_{start}, \alpha) := \sum_{k=0}^{N-1} \text{CVaR}\alpha(L_k) \
& \text{s.t.} \quad x_0 = x{start}, \, x_N = x_{goal}, \, N \leq N_{max}, \
& \quad x_k \in X_{free}, \, L_k = \ell(p[k]), \, \forall k \in \mathbb{Z}{0,N{max}-1}.
\end{aligned}
]
Probabilistic Guarantee on the Optimal (L_{worst}) Value
A probabilistic bound on the optimal worst-case path length (L_{worst}^*) is derived using the Kullback–Leibler (KL) divergence. The bound provides a formal confirmation of the probabilistic robustness of the risk-sensitive approach.
The RA-RRT* Planning Algorithm
The RA-RRT algorithm adapts the RRT algorithm to the stochastic setting by selecting nodes at each sampling iteration to minimize the empirically-computed CVaR(\alpha). The algorithm involves sampling a random node (x{rand}), finding the nearest node (x_{nearest}), and steering towards (x_{rand}) to obtain a new node (x_{new}). The algorithm then computes the VaR(\alpha) and CVaR(\alpha) for each path segment and selects the node with the minimum CVaR(_\alpha). The tree is updated accordingly, ensuring collision-free paths.
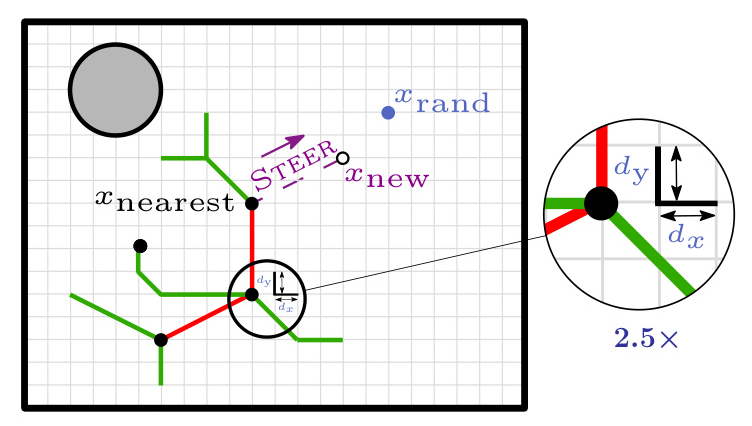
Algorithmic Complexity of the RA-RRT* Algorithm
The RA-RRT algorithm maintains linear query time and space complexity, similar to the RRT algorithm. However, the processing time complexity is log-linear due to the additional steps of computing VaR(\alpha) and CVaR(\alpha).

Numerical Simulations
Planning Environment
The planning environment is represented by a planar grid with sufficient discretization. The robot can steer towards uniformly-sampled nodes within a prescribed threshold, ensuring collision-free transitions.
Results & Discussions
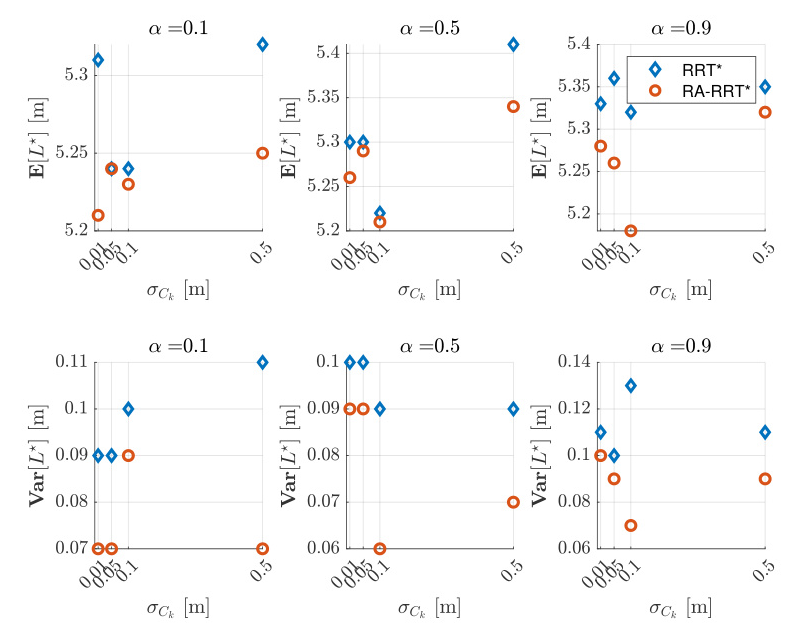
The simulation results demonstrate that the RA-RRT algorithm yields paths with lengths that are significantly less sensitive to variations in the noise parameter, providing robustness to environmental uncertainty. The RA-RRT algorithm also shows reduced planner failure rates compared to the RRT* algorithm.
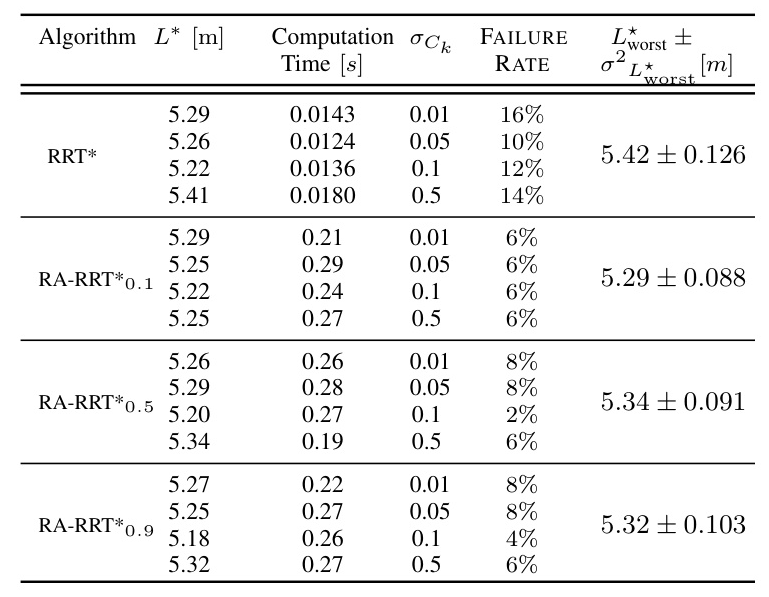
Worst-Case SSP Planning Performance
The RA-RRT algorithm exhibits smaller variability in mean path length and reduced variance compared to the RRT baseline. The algorithm also shows a lower failure rate and shorter worst-case path lengths under increasing noise.
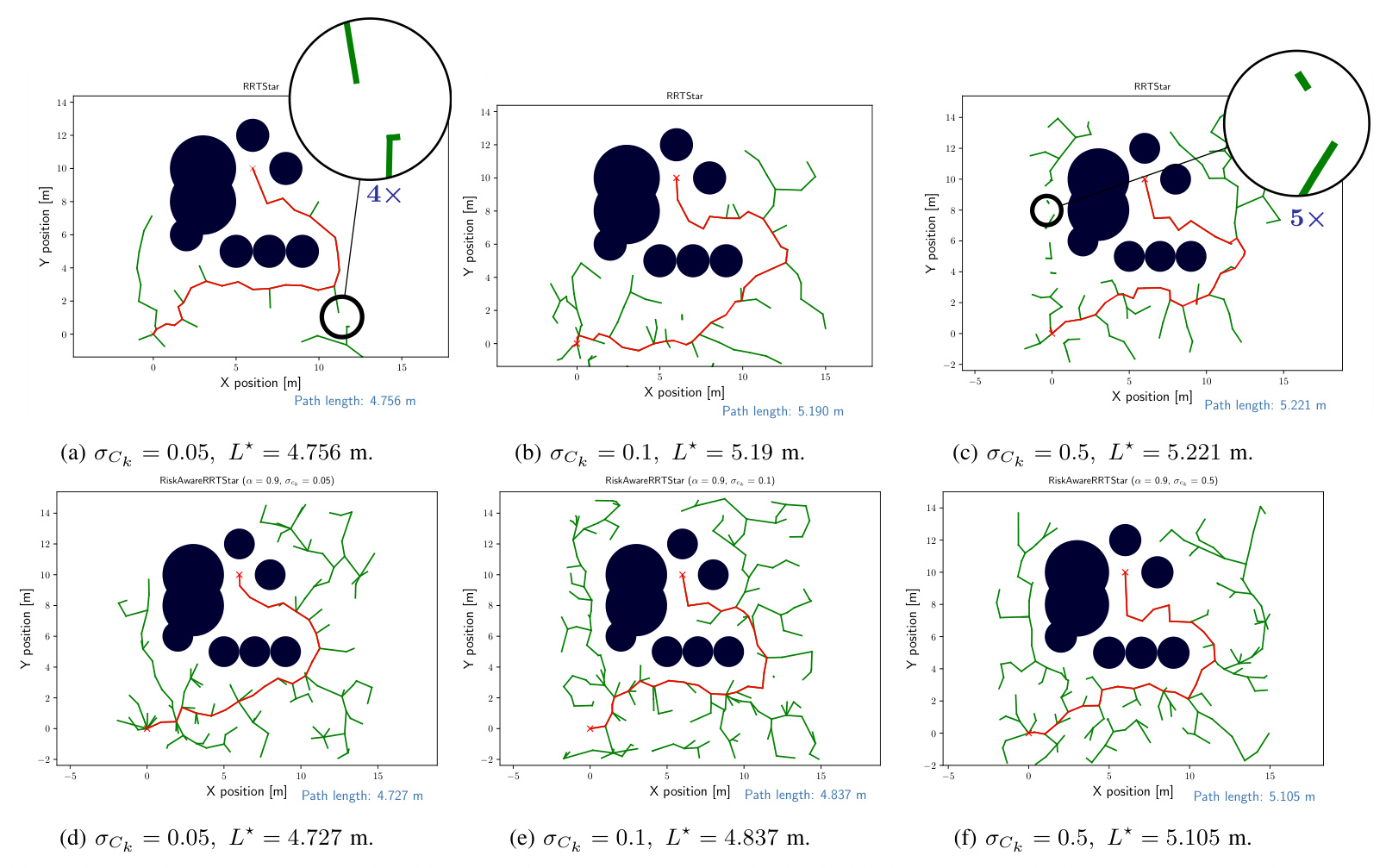
Assessing the Cost of Risk-Sensitive SSP Planning
The RA-RRT* algorithm incurs slightly higher computation time but is less sensitive to noise variations, resulting in shorter path lengths and reduced failure rates.
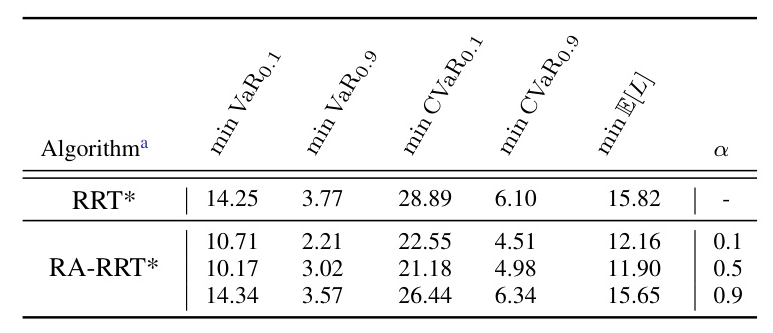
Performance at the Extremities of Uncertainty
At low noise levels, the RA-RRT algorithm performs similarly to the RRT algorithm. At high noise levels, the RA-RRT algorithm shows less severe performance degradation compared to the RRT algorithm.
Concluding Remarks
The RA-RRT algorithm provides a probabilistically-robust solution to SSP problems by incorporating risk-sensitive optimization. The algorithm maintains comparable query time and memory space complexity to the RRT algorithm while significantly reducing planner failure rates and providing robustness to environmental uncertainty. Future work will explore extensions to dynamic and noisy environments and non-Gaussian noise models.

