Authors:
Matthew Morris、David J. Tena Cucala、Bernardo Cuenca Grau、Ian Horrocks
Paper:
https://arxiv.org/abs/2408.10261
Introduction
Knowledge graphs (KGs) are structured knowledge bases where nodes and edges represent entities and their relationships, respectively. They are widely used in various applications, but often suffer from incompleteness. To address this, the field of KG completion has emerged, aiming to predict missing facts in KGs. Graph neural networks (GNNs), particularly Relational Graph Convolutional Networks (R-GCNs), have shown promise in this area. However, the explainability of their predictions remains a challenge. This study investigates whether R-GCNs can learn sound rules that explain their predictions and proposes methods to extract and verify such rules.
Related Work
Knowledge Graph Completion
KG completion is typically approached as a classification problem, where the goal is to predict whether a candidate fact holds in the completion of an incomplete KG. Various methods have been proposed, including embedding-based approaches, tensor products, recurrent neural networks, and differentiable reasoning. Among these, GNNs, especially R-GCNs, have gained significant attention.
Explainability in GNNs
The lack of explainability in GNNs has led to efforts to explain their predictions using logic-based formalisms like Datalog. Previous works have focused on extracting Datalog rules from certain subclasses of GNNs, ensuring that the rules are sound and complete with respect to the model. However, these methods often impose restrictions on model weights and aggregation functions, limiting their applicability to popular models like R-GCNs.
Research Methodology
Sum-GNNs
This study focuses on sum-GNNs, a variant of GNNs that use sum aggregation without restrictions on model weights. The goal is to identify output channels that exhibit monotonic behavior, allowing for the extraction of sound Datalog rules. The study also aims to identify unbounded channels for which no sound Datalog rule exists, indicating non-monotonic behavior.
Soundness and Completeness
A Datalog rule is sound for a sum-GNN if every fact derived by the rule is also predicted by the GNN. Conversely, a rule is complete if every fact predicted by the GNN is derived by the rule. The study provides methods to verify the soundness of Datalog rules for sum-GNNs.
Experimental Design
Datasets
The experiments use benchmark datasets (WN18RRv1, FB237v1, NELLv1) and datasets created using the LogInfer framework, which augments datasets with consequences of Datalog rules. The datasets are split into training, validation, and test sets, with negative examples generated using predicate corruption.
Training Paradigms
The study trains sum-GNNs with ReLU activation functions and biases, using binary cross-entropy loss and the Adam optimizer. Two variations to the training paradigm are proposed to encourage the learning of sound rules:
1. MGCN: Clamps all negative weights to zero during training, ensuring monotonic behavior.
2. R-X: Iteratively clamps weights below a certain threshold to zero, balancing model accuracy and the number of sound rules.
Results and Analysis
Monotonic LogInfer Datasets
The results show that R-GCNs, when trained in the standard way, do not learn any sound rules, even with near-perfect accuracy on monotonic datasets. In contrast, MGCNs, which enforce monotonic behavior, learn many sound rules and achieve high accuracy on test sets.
Benchmark Datasets
On benchmark datasets, R-GCNs achieve higher AUPRC on validation sets but lower accuracy on test sets compared to MGCNs. The R-X models demonstrate a trade-off between accuracy and the number of sound rules, with higher thresholds leading to more sound rules but lower accuracy.
Mixed LogInfer Datasets
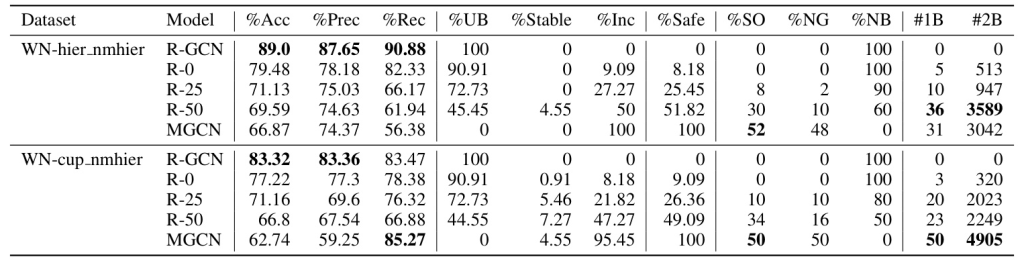
In mixed datasets with both monotonic and non-monotonic rules, R-GCNs again fail to learn sound rules. MGCNs achieve high recall but low precision, indicating that they learn versions of non-monotonic rules without negation, leading to false positives.
Channel Classification
The classification of channels into unbounded, stable, and increasing almost always adds up to 100%, indicating that the proposed methods effectively characterize channel behavior. The study also shows that the more complex classification into stable/increasing/decreasing/undetermined is necessary for accurate rule extraction.
Overall Conclusion
This study demonstrates that R-GCNs, when trained in the standard way, do not learn sound rules, raising concerns about their generalizability and explainability. The proposed training variations, MGCN and R-X, provide alternatives that encourage the learning of sound rules, with MGCNs being effective for monotonic datasets and R-X models offering a balance between accuracy and rule extraction. Future work will explore other GNN architectures, extend rule extraction to non-monotonic logics, and consider relaxed definitions of soundness.