Authors:
Maris F. L. Galesloot、Marnix Suilen、Thiago D. Simão、Steven Carr、Matthijs T. J. Spaan、Ufuk Topcu、Nils Jansen
Paper:
https://arxiv.org/abs/2408.08770
Introduction
Partially observable Markov decision processes (POMDPs) are a fundamental model for decision-making under uncertainty. They require policies that select actions based on limited state information to achieve specific objectives, such as minimizing expected costs. Traditional POMDPs assume precise knowledge of transition and observation probabilities, which is often unrealistic due to data limitations or sensor inaccuracies. Robust POMDPs (RPOMDPs) address this by incorporating uncertainty sets for these probabilities, optimizing policies against the worst-case scenarios within these sets.
Challenges in RPOMDPs
Finding robust policies for RPOMDPs is challenging due to the need to optimize against the worst-case instances of uncertainty sets. Evaluating a policy’s performance in an RPOMDP is complex because it is unclear which instance from the uncertainty sets to sample. This makes the use of recurrent neural networks (RNNs) in planning settings difficult, as they require guarantees on worst-case performance. Finite-state controllers (FSCs) offer a structured way to represent policies and allow for precise numerical evaluation through robust dynamic programming.
Contributions
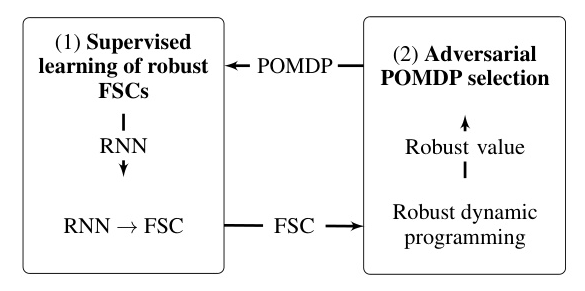
The paper introduces the Pessimistic Iterative Planning (PIP) framework, which combines the representational power of RNNs with the exact robust evaluation of FSCs. The main contributions are:
- Pessimistic Iterative Planning for RPOMDPs: The PIP framework iteratively solves POMDPs within the uncertainty set of the RPOMDP, finding adversarial instances to the current policy.
- RFSCNET Algorithm: An RNN-based algorithm that trains an RNN on data collected from supervision policies optimized for adversarial POMDPs, extracting FSCs for robust evaluation and adversarial POMDP selection.
Preliminaries
Definition of POMDP
A POMDP is defined as a tuple ( M = \langle S, A, T, Z, O, C \rangle ), where:
– ( S ), ( A ), ( Z ) are finite sets of states, actions, and observations.
– ( T: S \times A \rightarrow \Delta(S) ) is the probabilistic transition function.
– ( O: S \rightarrow Z ) is the deterministic state-based observation function.
– ( C: S \times A \rightarrow \mathbb{R}_{\geq 0} ) is the cost function.
Policies and Expected Costs
A policy ( \pi ) maps histories to distributions over actions. The objective is to find a policy that minimizes the expected cumulative cost of reaching goal states. For POMDPs, finding optimal policies is undecidable, so approximations with finite memory are used.
Finite-State Controllers (FSCs)
An FSC is a tuple ( \pi_f = \langle N, n_0, \delta, \eta \rangle ), where ( N ) is a finite set of memory nodes, ( n_0 ) is the initial node, ( \delta ) is the stochastic action function, and ( \eta ) is the deterministic memory update.
Recurrent Neural Networks (RNNs)
RNNs are state machines parameterized by differential functions, used to learn information about the history. They consist of an internal memory update and a policy network that maps histories to distributions over actions.
Robust Markov Models
Definition of RMDP
A robust MDP (RMDP) with interval uncertainty is defined as ( U = \langle S, A, T, C \rangle ), where ( T ) maps each transition to a probability interval or zero. The uncertainty is resolved in a game-like manner between the agent and nature.
Definition of RPOMDP
An RPOMDP with interval uncertainty is defined as ( M = \langle S, A, T, C, Z, O \rangle ), where ( T ) is the uncertain transition function. The robust SSP objective is to find a policy that minimizes the worst-case expected cost.
Supervised Learning of Robust FSCs
Data Generation
To train the RNN, a data set is generated by simulating the supervision policy on the current adversarial POMDP. The data set consists of histories and associated action distributions.
RNN Policy Training
The RNN policy is trained to minimize the distance between its distributions and those of the supervision policy. The training objective is optimized using backpropagation through time.
Extracting an FSC from an RNN
The hidden memory states of the RNN are clustered to find a finite-memory policy in the form of an FSC. Various clustering methods, such as quantized bottleneck networks (QBN) and k-means++, are considered.
Robust Policy Evaluation and Adversarial Selection of POMDPs
Robust Policy Evaluation
The performance of an FSC in an RPOMDP is evaluated using robust dynamic programming on a product Markov chain. This provides a conservative bound on the policy’s value.
Finding Adversarial POMDP Instances
A linear program is constructed to find a new POMDP instance that constitutes the local worst-case instance for the current policy. This instance is used in the next iteration of the learning scheme.
Experimental Evaluation
The performance of RFSCNET is evaluated on four benchmark environments: Aircraft, Avoid, Evade, and Intercept. The results show that RFSCNET improves robustness against model uncertainty and outperforms a baseline method and a state-of-the-art solver in several cases.
Robustness
RFSCNET incurs lower expected costs on average than the baseline in two out of four environments, demonstrating improved robustness.
Configuration Sensitivity
RFSCNET consistently outperforms the baseline across various configurations, showing that the choice of supervision policies and clustering methods affects performance.
Comparison with State-of-the-Art
RFSCNET outperforms the state-of-the-art SCP method in several benchmarks, particularly when the memory size is increased.
Memory Size Sensitivity
RFSCNET is not sensitive to memory over-specification, exhibiting consistent performance across different memory sizes.
Conclusion
The PIP framework and RFSCNET algorithm provide a novel approach to finding robust policies for RPOMDPs by combining RNNs and FSCs. The experimental results demonstrate the effectiveness of this approach in improving robustness and outperforming existing methods. Future work will explore the generalization capabilities of RNN policies in more complex domains.
Illustrations