Authors:
Valentin Zech、Niclas Boehmer、Edith Elkind、Nicholas Teh
Paper:
https://arxiv.org/abs/2408.11017
Multiwinner Temporal Voting with Aversion to Change: An In-Depth Analysis
Introduction
In the realm of multiwinner voting, the dynamic nature of voter preferences poses significant challenges. This study, titled “Multiwinner Temporal Voting with Aversion to Change,” delves into the complexities of two-stage committee elections where voters’ preferences evolve over time. The primary objective is to identify a winning committee in the second stage that maintains substantial overlap with the first-stage committee, thereby ensuring stability and continuity.
Background
The study is motivated by practical scenarios such as local town council elections, where maintaining continuity in committee membership is crucial for leveraging existing expertise and ensuring stable governance. The problem is framed within the context of multiwinner temporal voting, a natural extension of the multiwinner voting model, where the goal is to elect a committee at each timestep while minimizing changes in committee membership.
Related Work
The study builds on the foundational work of Bredereck et al. and others who have explored various aspects of multiwinner voting and temporal voting. Key differences in this study include the focus on a large class of popular voting rules, fixed committee sizes, and the realistic assumption that second-stage preferences are not known initially.
Previous Studies
- Bredereck et al. (2018): Investigated models where committees need to satisfy a lower bound on their score and subsequent committees need not be of the same size.
- Elkind et al. (2020): Provided a survey on multiwinner voting models.
- Faliszewski et al. (2022): Studied robustness in temporal voting, focusing on the minimum number of changes required to alter the election outcome.
Contributions
This study extends the existing body of work by providing a full complexity classification for Thiele rules and their greedy variants, exploring parameterized complexity, and conducting experimental analysis to measure the impact of changes in voter preferences on committee membership.
Research Methodology
The study focuses on two-stage elections using a fixed voting rule to select a winning committee at each stage. Voters have approval preferences that may evolve between stages. The goal is to identify a second-stage committee that wins under the new preferences while maximizing overlap with the first-stage committee.
Thiele Rules
Thiele rules, a well-known class of voting rules, are central to this study. These rules include:
– Approval Voting (AV)
– Proportional Approval Voting (PAV)
– Chamberlin–Courant Approval Voting (CCAV)
The study also considers greedy variants of these rules, which are computationally more tractable.
Decision Problem
The primary decision problem, termed Resilient Committee Elections (R-RCE), is defined as follows:
– Input: Elections ( E ) and ( E’ ), committee size ( k ), winning committee ( S ), and distance bound ( \ell ).
– Question: Does there exist a committee ( S’ ) in ( E’ ) such that the distance between ( S ) and ( S’ ) is at most ( \ell )?
Experimental Design
The experimental analysis aims to complement the theoretical findings by measuring the practical impact of changes in voter preferences on committee membership.
Models for Generating Preferences
Two models are used to generate approval-based preferences:
1. 1D-Euclidean Model: Voters and candidates are assigned points in the interval [0, 1], and a voter approves a candidate if the distance between their points is within a specified radius.
2. 2D-Euclidean Model: Voters and candidates are assigned points in the unit square [0, 1] × [0, 1], with approval based on Euclidean distance.
Change Operations
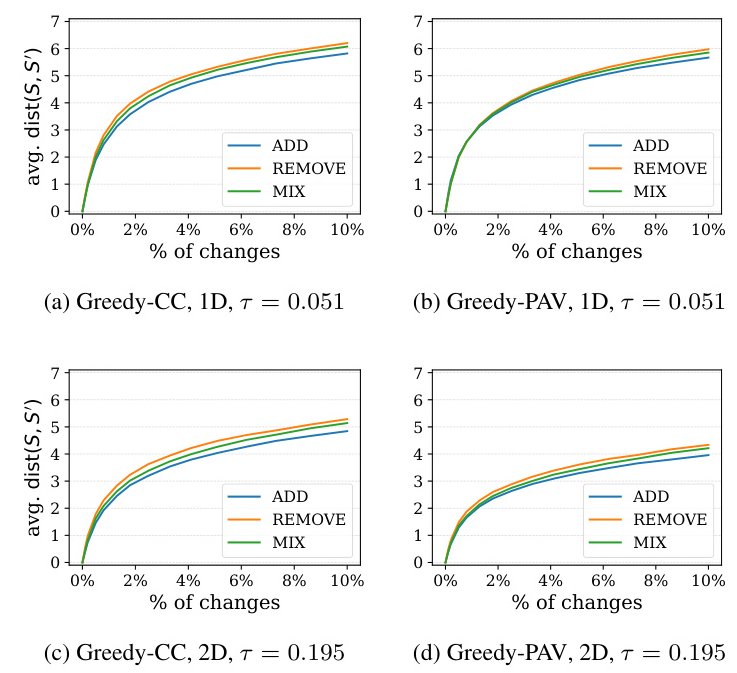
Three types of changes are considered:
– ADD: Adding new approvals.
– REMOVE: Removing existing approvals.
– MIX: A combination of adding and removing approvals.
Experimental Questions
The experiments focus on three key questions:
1. Resilience: How much do winning committees change when votes change?
2. Role of Ties: How effective is lexicographical tie-breaking in maintaining committee continuity?
3. Replacement Patterns: Which committee members are more likely to be replaced when changes occur?
Results and Analysis
Resilience of Greedy Thiele Rules
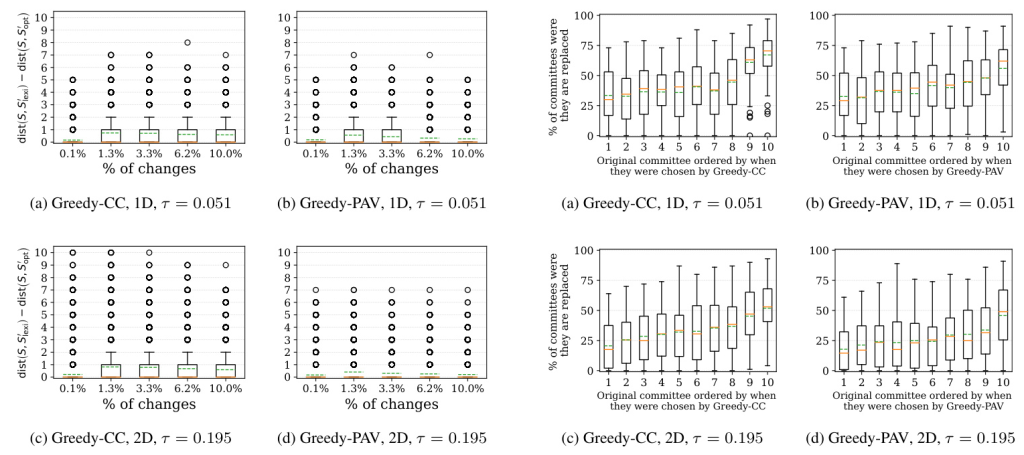
The experiments reveal that winning committees under Greedy-CC and Greedy-PAV are highly non-resilient. Even small changes in voter preferences lead to significant changes in committee membership.
Role of Ties
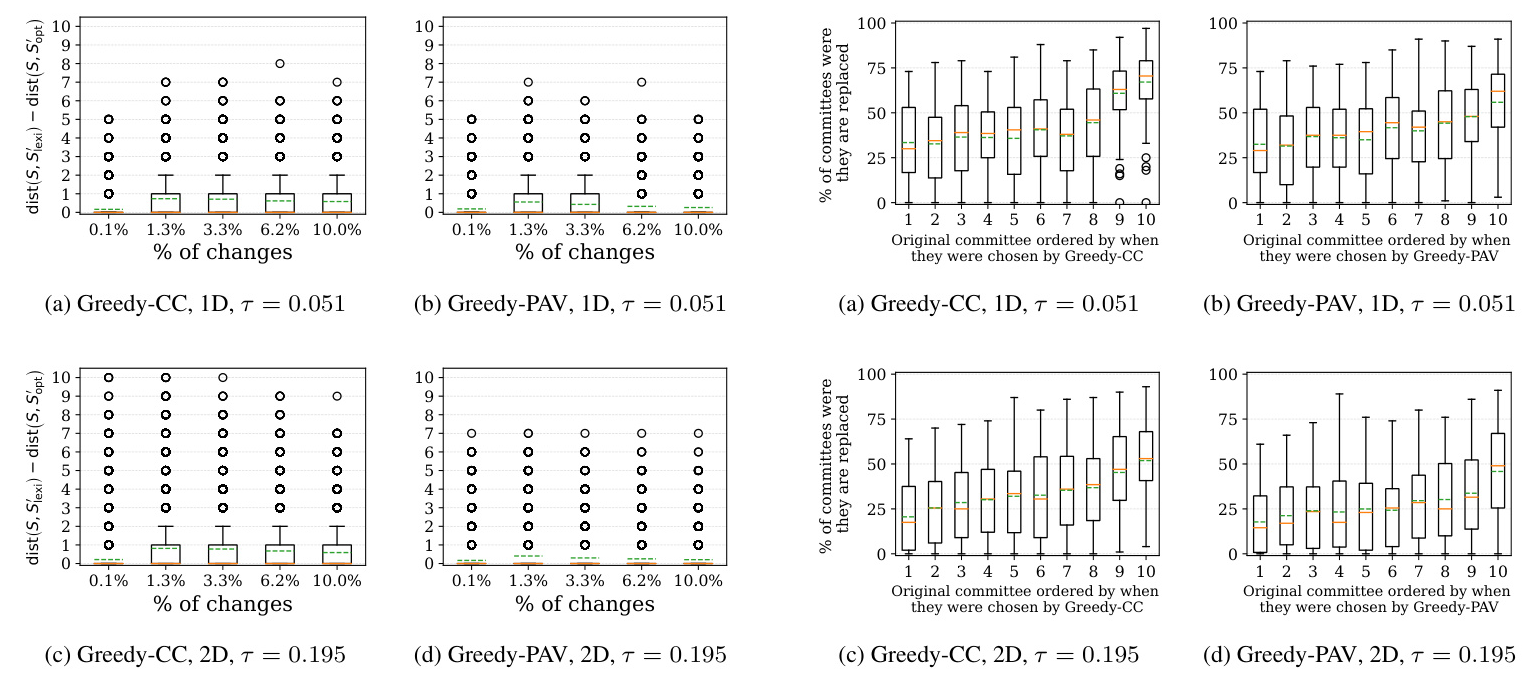
The analysis shows that lexicographical tie-breaking is not a reliable heuristic for maintaining committee continuity. There are significant differences in the contiguity offered by lexicographically chosen committees compared to optimally chosen ones.
Replacement Patterns
The experiments indicate a weak correlation between the round in which a candidate was chosen and the likelihood of their replacement. Candidates chosen in later rounds are slightly more likely to be replaced.

Overall Conclusion
The study provides a comprehensive analysis of the complexity and practical implications of multiwinner temporal voting with aversion to change. The findings highlight the challenges in maintaining committee continuity and the limitations of existing heuristics like lexicographical tie-breaking. Future work could explore weighted costs for candidate replacement and investigate the resilience of other voting rules designed for temporal settings.
This study contributes valuable insights into the dynamics of multiwinner temporal voting and offers a foundation for further research in this area.
Code:
https://github.com/valentinzech/ecai_multiwinner_temporal_voting_with_aversion_to_change