Authors:
Hong Xie、Jinyu Mo、Defu Lian、Jie Wang、Enhong Chen
Paper:
https://arxiv.org/abs/2408.10865
Introduction
In the realm of distributed selection problems, the multi-player multi-armed bandit (MAB) model has been a cornerstone for addressing issues such as channel access in cognitive radio applications. However, traditional models often fall short when applied to real-world scenarios like ridesharing or food delivery services, where requests arrive stochastically and independently of the number of players. This paper introduces a novel variant of the multi-player MAB model that captures these stochastic arrivals and proposes efficient algorithms to optimize the allocation of requests to players.
Related Work
Stochastic Multi-player MAB with Collision
The literature on multi-player MAB models primarily focuses on scenarios where players know if they encounter a collision. Various algorithms have been proposed to minimize regret in these settings:
- Time-division fair sharing algorithm by Liu et al. [11] achieves logarithmic total regret.
- Logarithmic total regret algorithms by Anandkumar et al. [1] and Rosenski et al. [16].
- Communication-free algorithms by Besson et al. [4] and Lugosi et al. [12] that use collision information as a means of communication.
Stochastic Multi-player MAB without Collision
In settings where players receive independent rewards upon collision, algorithms like DD-UCB by Martínez-Rubio et al. [14] and MP-UCB by Dubey et al. [8] have been proposed. These algorithms utilize communication graphs to share reward information among players.
Summary of Differences
Unlike previous works, this paper formulates a new variant of the multi-player MAB model that captures the stochastic arrival of requests and the allocation policy. The proposed algorithms introduce novel ideas for searching and committing to the optimal arm pulling profile and achieving consensus among players with different estimates.
Research Methodology
Platform Model
The platform consists of requests, players, and a platform operator. The arrival of requests is modeled by a finite set of arms, each characterized by a pair of random vectors representing the stochastic request and reward distributions. Players can pull only one arm per time slot, and the platform operator ensures that each player serves at most one request.
Problem Formulation
The objective is to maximize the total reward across all players over a given time horizon. The optimal arm pulling profile is defined as the one that maximizes the total reward. The challenge lies in searching for this optimal profile and ensuring that players commit to it without communication.
Experimental Design
Searching the Optimal Arm Pulling Profile
A greedy algorithm (Algorithm 1) is proposed to locate one of the optimal arm pulling profiles with a computational complexity of O(KM). The algorithm sequentially adds players to arms based on the largest marginal reward gain.
markdown
Algorithm 1 OptArmPulProfile (µ, e P )
1: ∆m ←µm, ∀m ∈M, ngreedy,m ←0, ∀m ∈M
2: for k = 1, . . . , K do
3: i = arg maxm∈M ∆m (if there is a tie, breaking it by an arbitrary tie breaking rule)
4: ngreedy,i ←ngreedy,i + 1, ∆i ←µiPi,ngreedy,i
5: end for
6: return ngreedy = [ngreedy,m : ∀m ∈M]
Committing to Optimal Arm Pulling Profile
An iterative distributed algorithm (Algorithm 2) is designed for players to commit to the optimal arm pulling profile. The algorithm ensures that players commit to the same profile in a constant number of rounds in expectation.
markdown
Algorithm 2 CommitOptArmPulProfile (k, n∗, Tstart)
1: ck←0, ∀k∈K, n− t,m←n∗ m, ∀m∈M, n+ t,m←0, ∀m∈M
2: for t = Tstart, . . . , T do
3: if ck ̸= 0 then
4: at+1,k ←at,k
5: else if n∗ at,k ≥nt,at,k then
6: ck ←at,k, at+1,k ←at,k
7: else
8: for m = 1, . . . , M do
9: if n∗ m ≥nt,m then
10: n+ t,m ←nt,m, n− t,m ←n∗ m −n+ t,m
11: end if
12: end for
13: N − t = P m∈M n− t,m. at+1,k←m, w.p. n− t,m/N − t
14: end if
15: player k pulls arm at+1,k, player k receive nt+1
16: end for
Online Learning Algorithm
The online setting is addressed using the explore-then-commit (ETC) framework. During the exploration phase, players estimate the request and reward distributions. An iterative distributed algorithm (Algorithm 4) ensures that players reach a consensus on the optimal arm pulling profile.
markdown
Algorithm 4 Consensus(k, n∗(k))
1: vboard,k ← 0, vboard,k ← ∅, Num←0
2: for t = T0 + 1, . . . , T0 + M do
3: player k pulls arm (n∗ t−T0 (k) mod M + 1)
4: if max{m|nt,m > 0} − min{m|nt,m > 0} == 1 then
5: Update borderline elem. vboard,k←(vboard,k, t − T0)
6: vboard,k ← vboard,k ∪ {(t − T0, n∗ t−T0 (k) mod M+1=min{m|nt,m>0})}
7: else if max{m|nt,m > 0} − min{m|nt,m > 0} > 1 then
8: vboard,k ← (vboard,k, t − T0), ∀k ∈ K
9: vboard,k ← vboard,k ∪ {(t − T0, n∗ (k) mod M+1=max{m|nt,m>0})}, ∀k ∈ K
10: end if
11: end for
12: for m = 1, . . . , M do
13: if {(m, n∗ m(k))} ∈ vboard,n then
14: n∗ m(k) ← n∗ m(k) − 1, Num←Num +1
15: end if
16: end for
17: vboard,n ← vboard,n sorted in descending order
18: n∗ vboard,k(i) ← n∗ vboard,k(i) + 1, ∀i = 1, . . . , Num
19: return n∗(k) = [n∗ m(k) : ∀m ∈ M]
Results and Analysis
Impact of Exploration Length
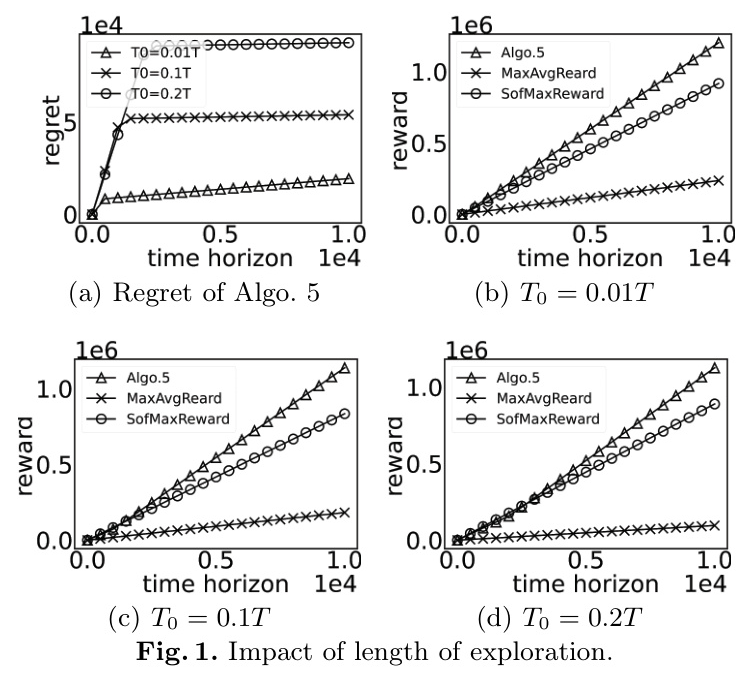
The length of the exploration phase significantly impacts the regret and total reward. As shown in Figure 1, the regret initially increases sharply during the exploration phase and then stabilizes during the committing phase. The algorithm achieves higher rewards compared to baseline methods.
Impact of Number of Arms
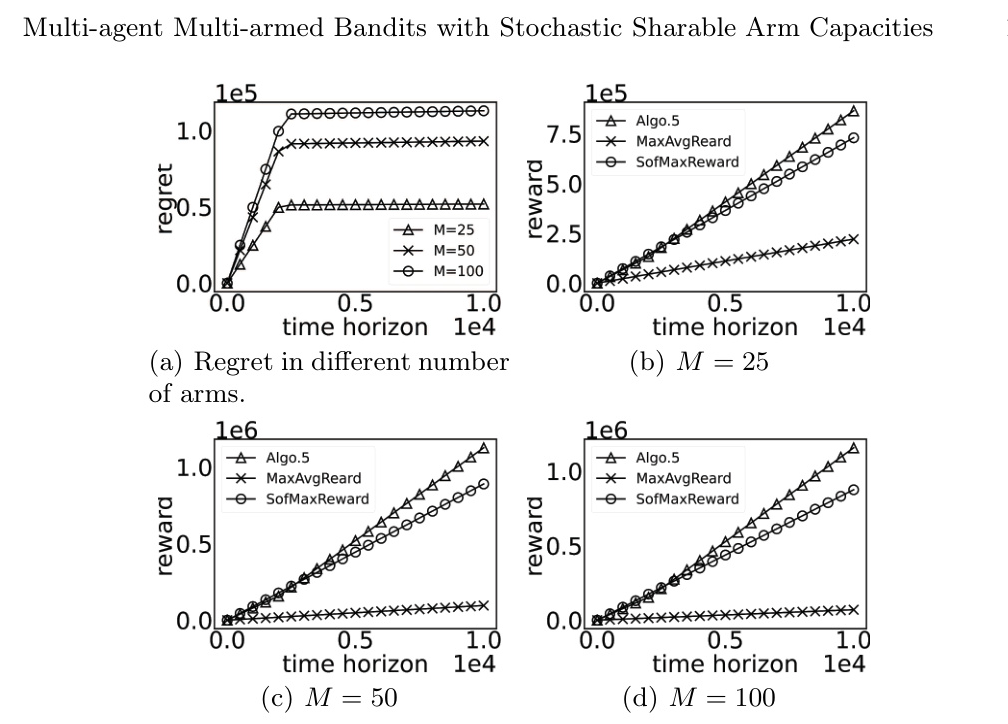
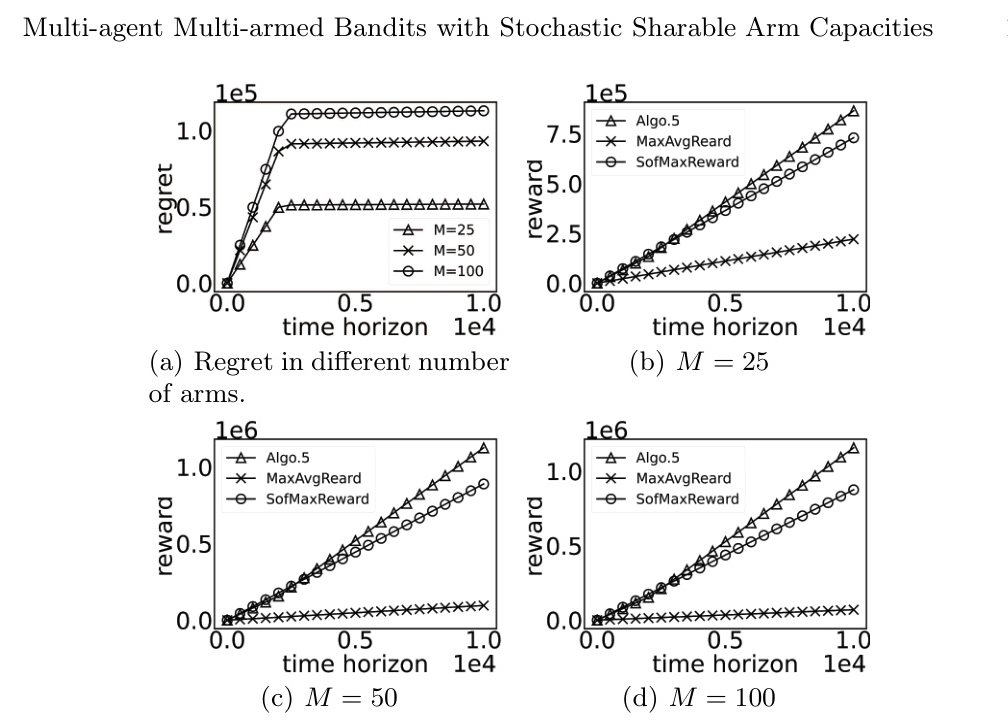
The algorithm’s performance remains robust across different numbers of arms. As shown in Figure 2, the regret curves exhibit similar behavior, validating the algorithm’s convergence properties.
Impact of Number of Players
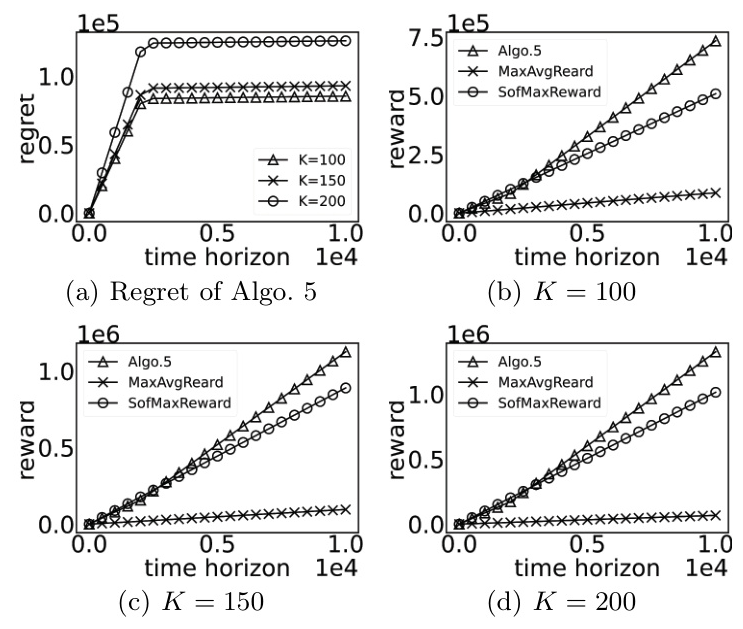
The algorithm also performs well with varying numbers of players. Figure 3 demonstrates that the regret curves stabilize after the exploration phase, and the algorithm consistently outperforms baseline methods in terms of total reward.
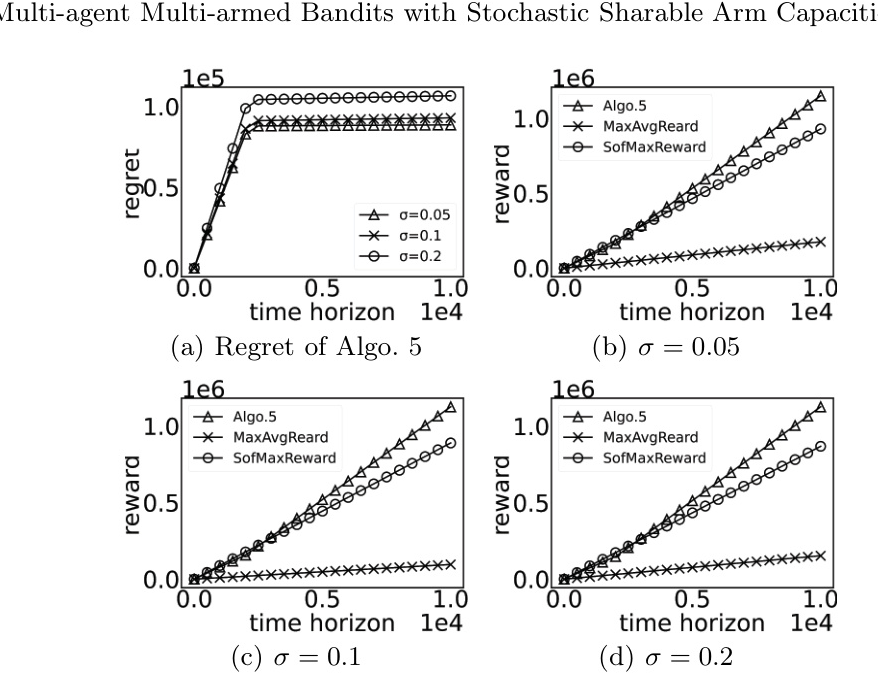
Impact of Standard Deviation
The algorithm’s performance is consistent across different levels of reward variability. Figure 4 shows that the regret curves stabilize after the exploration phase, and the algorithm achieves higher rewards compared to baseline methods.
Overall Conclusion
This paper introduces a new variant of the multi-player MAB model to address distributed selection problems with stochastic request arrivals. The proposed greedy algorithm efficiently locates one of the optimal arm pulling profiles, and the iterative distributed algorithm ensures that players commit to this profile with a constant number of rounds in expectation. The exploration strategy allows players to estimate the optimal profile accurately, and the consensus algorithm guarantees agreement among players. Experimental results validate the efficiency and robustness of the proposed algorithms across various settings.