Authors:
Giovanni Varricchione、Natasha Alechina、Mehdi Dastani、Brian Logan
Paper:
https://arxiv.org/abs/2408.08059
Maximally Permissive Reward Machines: A Detailed Exploration
Introduction
Reward machines (RMs) are a powerful tool for defining temporally extended tasks and behaviors in reinforcement learning (RL). They represent tasks as sequences of abstract steps or phases, with transitions corresponding to high-level events in the environment. However, generating informative RMs can be challenging, and existing planning-based approaches often limit the flexibility of the learning agent by relying on a single plan. This paper introduces a novel approach to synthesizing RMs based on the set of partial-order plans for a goal, resulting in “maximally permissive” reward machines (MPRMs). Theoretical and experimental results demonstrate that MPRMs enable higher rewards and greater flexibility compared to single-plan RMs.
Preliminaries
Reinforcement Learning
In RL, agents learn to act within a Markov Decision Process (MDP) defined by states (S), actions (A), a reward function (r), a transition function (p), and a discount factor (\gamma). The agent’s goal is to learn an optimal policy (\rho) that maximizes the expected discounted future reward from any state (s \in S).
Labelled MDPs
A labelled MDP includes a labelling function (L) that maps each state to a set of propositional symbols, linking the low-level MDP with high-level planning domains and reward machines.
Reward Machines
RMs define non-Markovian reward functions via finite state automata. Training with RMs involves the product of the labelled MDP and the RM, forming a Markov Decision Process with a Reward Machine (MDPRM).
Symbolic Planning
Symbolic planning involves a planning domain (D) with fluents (propositions) and planning actions. Planning states are subsets of fluents, and actions have preconditions and effects. A planning task is defined by a domain (D), an initial state (S_I), and a goal (G). Plans can be sequential or partial-order, with partial-order plans allowing greater flexibility.
Maximally Permissive Reward Machines
Construction of MPRMs
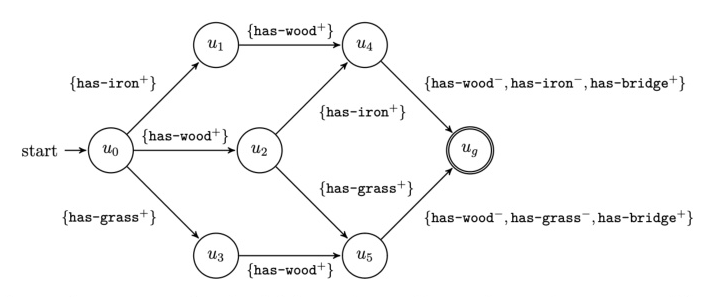
MPRMs are synthesized from the set of all partial-order plans for a planning task. The states of the MPRM correspond to all possible prefixes of planning states across all partial-order plans. Transitions occur based on observed propositional symbols, and rewards are given based on the completion of goal states.
Theoretical Analysis
The paper proves that learning with MPRMs results in higher rewards compared to single-plan RMs. Theorem 3.1 shows that the optimal policy learned using MPRMs is at least as good as those learned using single partial-order or sequential plans. Theorem 3.3 establishes that MPRMs can learn goal-optimal policies if the planning domain is adequate for the goal.
Empirical Evaluation
Experimental Setup
The evaluation uses three tasks in the CRAFTWORLD environment: building a bridge, collecting gold, and collecting gold or a gem. For each task, MPRMs and RMs based on single partial-order and sequential plans are synthesized. Agents are trained using Q-learning over the resulting MDPRMs.
Results
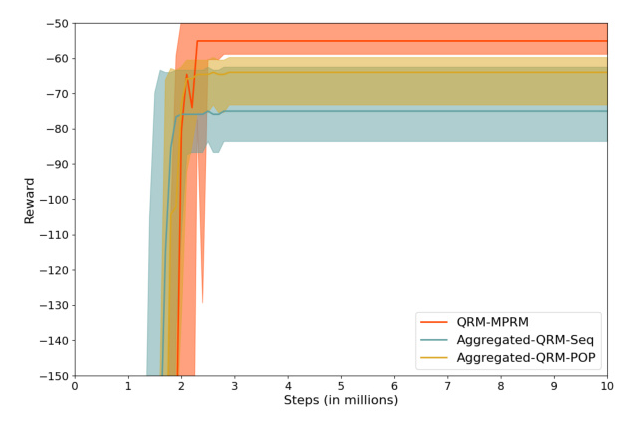
The results show that agents trained with MPRMs outperform those trained with single-plan RMs in all tasks. However, MPRMs converge more slowly due to increased flexibility.
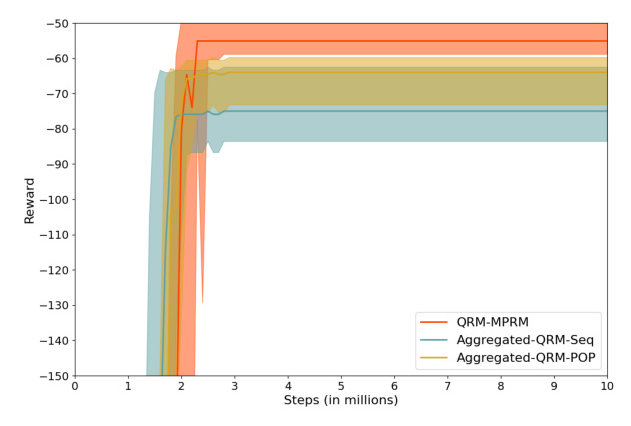
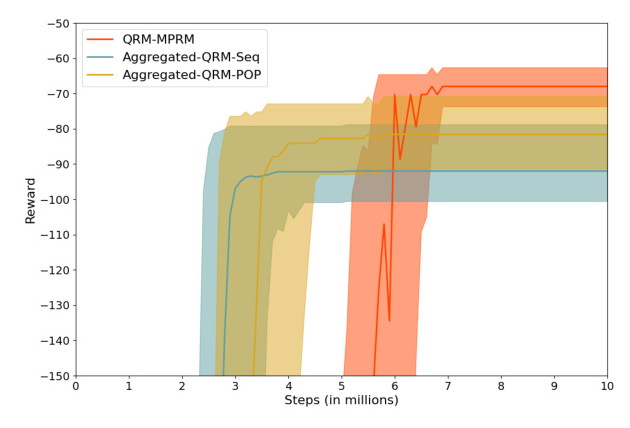
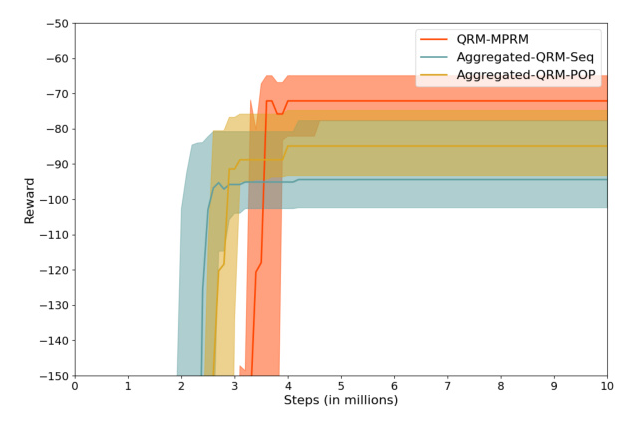
Illustration of Agent Behavior
Figure 5 illustrates the behavior of agents trained with MPRMs and single partial-order plans on the gold-or-gem task. The MPRM agent achieves the goal efficiently by choosing the optimal plan based on its position.

Related Work
The paper discusses related work on reward machines in single-agent and multi-agent RL, as well as approaches to synthesizing and learning RMs from experience. It also covers planning-based approaches to RL and the integration of planning with options.
Conclusions
The proposed approach synthesizes maximally permissive reward machines using the set of partial-order plans for a goal. Theoretical and experimental results demonstrate that MPRMs enable agents to learn better policies compared to single-plan RMs. Future work includes investigating top-k planning techniques and option-based approaches to learning, as well as evaluating the approach in continuous environments.
This detailed exploration of maximally permissive reward machines highlights their potential to enhance the flexibility and performance of reinforcement learning agents in complex environments.