Authors:
Shashank Kotyan、Pin-Yu Chen、Danilo Vasconcellos Vargas
Paper:
https://arxiv.org/abs/2408.09065
Introduction
Background
The rapid advancements in computer vision and deep learning have led to the development of powerful vision models capable of extracting intricate features from visual data. These models are central to various applications, from object recognition to image generation. Typically, their generalizability is measured through zero-shot classification performance, making the evaluation of vision models indirect. However, these evaluations often rely on a projection of the learned latent space, which may not fully capture the quality or nuances of the underlying representations and offer little insight into improving them.
Problem Statement
Understanding the structure and quality of a latent space is crucial for gaining insights into how vision models process and organize visual information. Traditional methods like t-SNE and UMAP offer visualizations of this high-dimensional space by reducing its dimensions. While these methods provide insights about a latent space, they are less effective when comparing multiple latent spaces. As vision models become more sophisticated, there is a growing need for methods that offer a more detailed and interpretable analysis of the latent space beyond mere visual inspection.
Related Work
Analyzing the Latent Space of Neural Networks
Analyzing the latent space of deep neural networks poses a significant challenge due to the high-dimensional nature of the features. Researchers have developed various dimensionality reduction techniques that allow for the visualization and interpretation of these complex spaces in lower dimensions, typically 2D or 3D. Among the most widely used techniques are t-SNE and UMAP, which are used for their ability to preserve local and global structures, respectively.
Dimensionality Reduction Techniques
Dimensionality reduction techniques like PCA, MDS, Diffusion Maps, and TriMap are part of a broader family of methods designed to make the high-dimensional latent space more interpretable by projecting it into a more manageable form. Interpretation using these techniques largely depends on the organization of the latent space. When the latent space is well-structured, these visualizations can be highly effective. However, where the latent space lacks a clear structure, the utility of these methods diminishes.
Visualization of Neural Network Features
Beyond dimensionality reduction, other approaches focus on visualizing the interactions between neural network features and the latent space. By analyzing the activation patterns of hidden units in response to specific inputs, researchers can gain insights into which features are emphasized by the network. Tools like Activation Atlas offer a way to explore how combinations of features are represented, further illuminating the structure of the learned latent space.
Challenges in Comparing Latent Spaces
These visualization techniques often involve complex hyperparameter tuning, making it difficult to achieve consistent and fair comparisons across different latent spaces, especially when comparing vision models with varying dimensionalities. The interpretability of these visualizations becomes increasingly complicated when multiple models are involved, as the differences in their latent space structures can lead to incomparable results.
Research Methodology
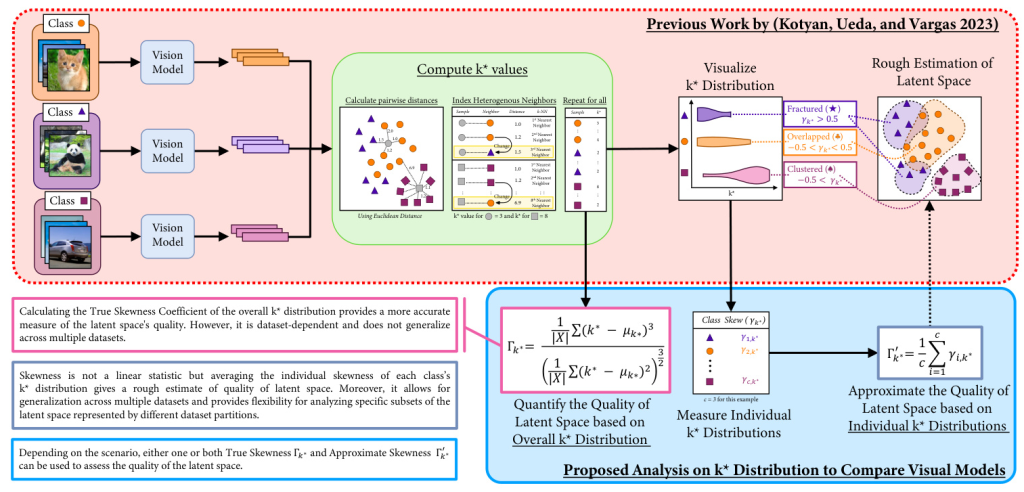
k* Distribution for Latent Space Analysis
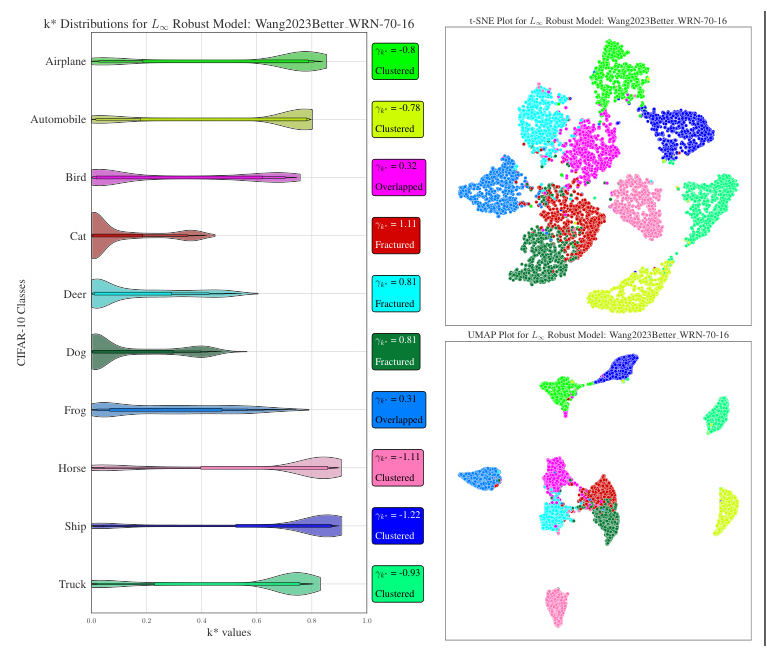
The k* distribution proposed by Kotyan, Ueda, and Vargas provides a robust method for analyzing the structure of hyperdimensional latent spaces learned by vision models, focusing on local neighborhood dynamics. This approach is instrumental in understanding how samples and clusters are distributed within the latent space by associating them with their respective concepts (classes).
Mathematical Framework
The k value represents the index of the kth nearest neighbor that belongs to a different concept (class) than the test sample. This value measures the neighborhood uniformity; a high k value suggests that a sample is surrounded by many neighbors from the same class, indicating a well-formed homogeneous cluster. Conversely, a low k* value points to the proximity of a neighbor from a different class, signaling potential overlap or a fragmented neighborhood.
Skewness Coefficient
The Skewness Coefficient of k distribution (γk˚) measures the asymmetry of the k distribution about its mean. Positive skewness indicates a distribution skewed towards lower k values, indicating fracturing, while negative skewness indicates a distribution skewed towards higher k values, indicating clustering. The True Skewness Coefficient Γk˚ and the Approximate Skewness Coefficient Γ 1 k˚ are used to quantify the quality of the latent space.
Experimental Design
Analyzing Robust Image Encoders
Experimental Setup
In this study, robust vision models available at RobustBench Library are evaluated. These models have been comprehensively evaluated through various adversarial attacks to be classified as robust. The repository offers pre-trained weights for these models, which are used for the analysis.
Results
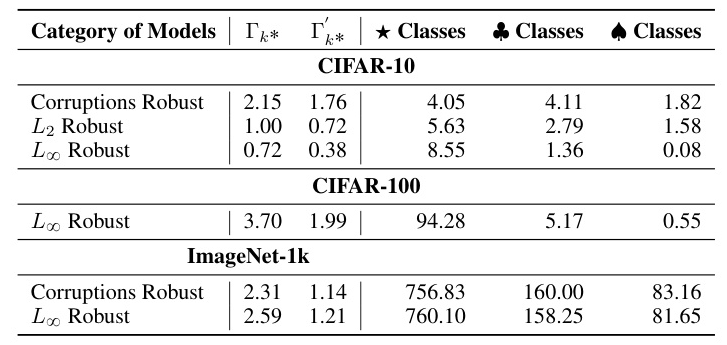
Comparing the k Distribution between different variants of robust models reveals significant differences. The k Distribution allows for a more objective comparison of the models, showing that more robust models tend to have less fracturing in the latent space.
Analyzing CLIP-based Image Encoders
Experimental Setup
Open CLIP models are utilized to evaluate CLIP-based vision models. These models have undergone extensive evaluation on various datasets, and the repository offers both evaluation scripts and pre-trained weights, which are leveraged for the analysis.
Results
A comparison of different Open CLIP models using the Approximate Skewness Coefficient Γ 1 k˚ shows that a lower Approximate Skewness Coefficient is associated with better accuracy in zero-shot classification across the evaluated datasets. However, this trend does not apply universally to all datasets.
Results and Analysis
Patterns in Latent Space Distribution
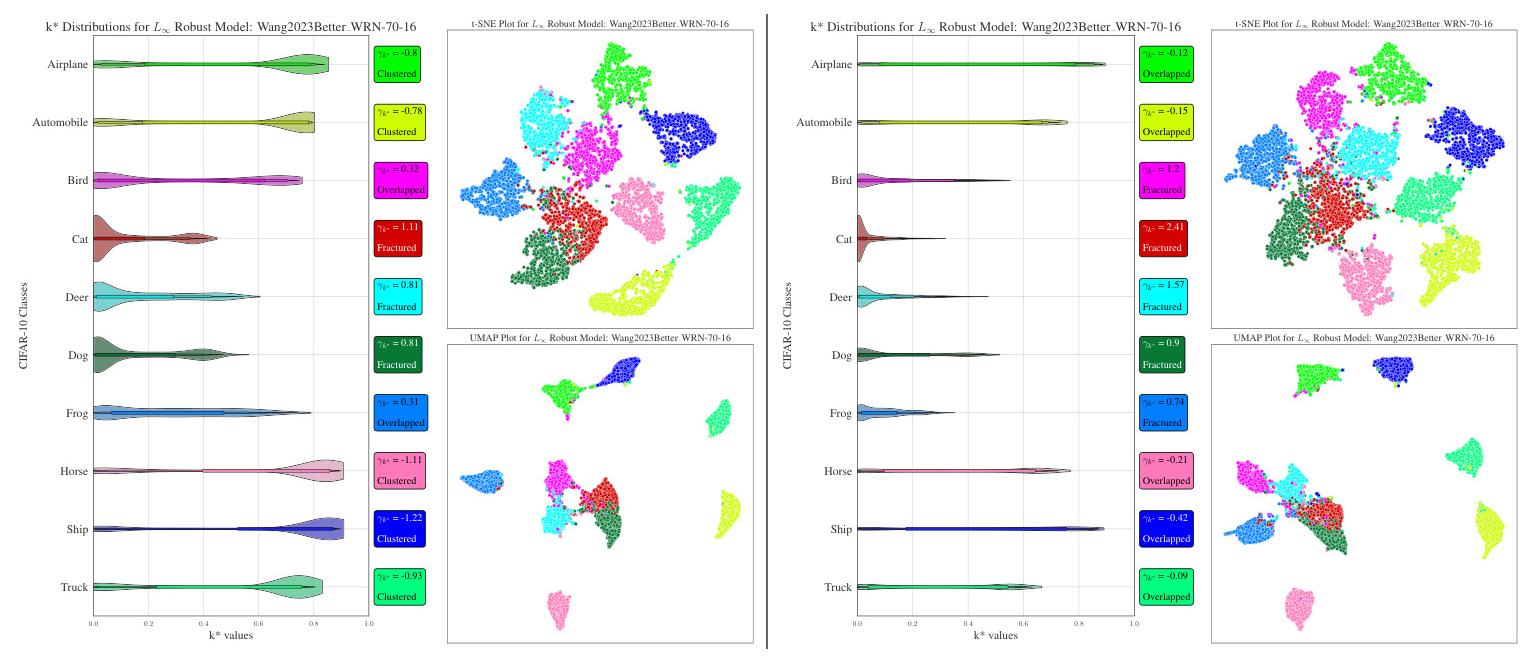
Fractured Distribution
In this latent space configuration, multiple clusters of testing samples are observable, each separated in the latent space. The k* distribution for this clustered distribution of samples in latent space is markedly positively skewed (γk˚ > 0.5).
Overlapped Distribution
This latent space configuration represents the scenario when samples from two or more classes overlap. The k* distribution appears nearly uniform (-0.5 < γk˚ < 0.5).
Clustered Distribution
A homogeneous cluster of testing samples is prevalent in this latent space arrangement. The k* distribution for this clustered distribution of samples in latent space is strongly negatively biased (γk˚ < -0.5).

Comparison of Robust Models
The analysis shows that the number of fractured classes increases in the order of L8 robust, L2 robust, and Corruptions robust. The comparison of the models based on the Average Skewness Coefficient Γ 1 k˚ over both Natural Accuracy and Robust Accuracy demonstrates that as models become more robust, they better interpret the concepts by improving the clustering of the concept’s samples.
Comparison of CLIP Models
The comparison of different Open CLIP models using the Approximate Skewness Coefficient Γ 1 k˚ shows that a lower Approximate Skewness Coefficient is associated with better accuracy in zero-shot classification across the evaluated datasets. However, this trend does not apply universally to all datasets.
Overall Conclusion
In this study, the k Distribution is utilized to directly examine the latent space of various types of vision models, revealing insights into how individual concepts are structured in these models’ latent spaces. By introducing skewness-based metrics, both true and approximate, the study quantifies the quality of these latent spaces. The findings highlight that current vision models often fragment the distributions of individual concepts within the latent space. However, as models improve in generalization and robustness, the degree of fracturing decreases. This suggests that better generalization and robustness are associated with a more coherent clustering of concepts in the latent space. The quantification of the analysis of k Distribution offers a direct and interpretable approach for comparing latent spaces, establishing a clear relationship between a model’s generalization, robustness, and the quality of its latent space.