Authors:
Paper:
https://arxiv.org/abs/2408.09158
Introduction
Background
Spatial-temporal forecasting, particularly in traffic prediction, has garnered significant attention due to its complex correlations in both space and time dimensions. Traditional methods often treat road networks as spatial-temporal graphs, addressing spatial and temporal representations independently. However, these approaches face challenges in capturing the dynamic topology of road networks, dealing with message passing mechanisms, and learning spatial and temporal relationships separately.
Problem Statement
Existing methods struggle with:
1. Capturing the dynamic topology of road networks.
2. Overcoming the over-smoothing problem in Graph Neural Networks (GNNs).
3. Learning spatial and temporal relationships separately, which requires more layers and increases computational complexity.
To address these limitations, this study proposes treating nodes in road networks at different time steps as independent spatial-temporal tokens and feeding them into a vanilla Transformer to learn complex spatial-temporal patterns. The proposed models, STformer and NSTformer, aim to achieve state-of-the-art performance with reduced computational complexity.
Related Work
Transformer in Traffic Forecasting
Transformers have become the de-facto standard in various applications, including traffic forecasting. Previous works have used attention-based models to separately learn spatial and temporal representations. However, these models still operate within the Spatial-Temporal Graph framework, which has inherent drawbacks.
Efficient Transformer
The self-attention mechanism in Transformers has quadratic complexity, which limits its performance with large inputs. Various methods, such as Nyströmformer, have been proposed to approximate self-attention with linear complexity, making it more feasible for large-scale applications.
Research Methodology
Problem Setting
The traffic forecasting task is defined as learning a mapping from past traffic flow to future traffic flow using neural networks. The road network is represented as a tensor, and the traffic flow over a period forms a spatial-temporal tensor.
Model Architecture
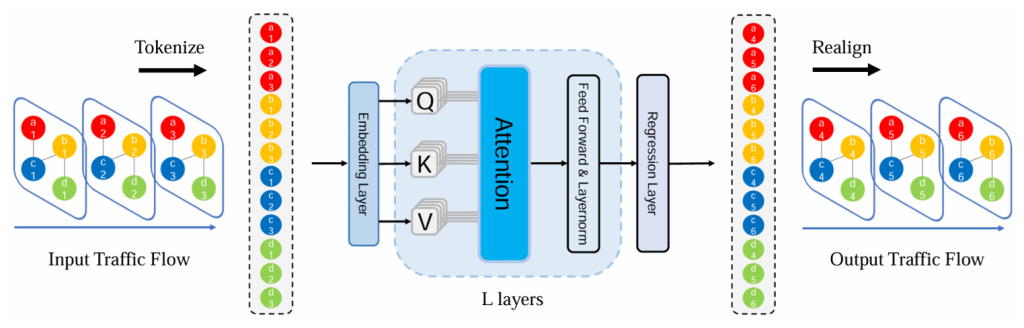
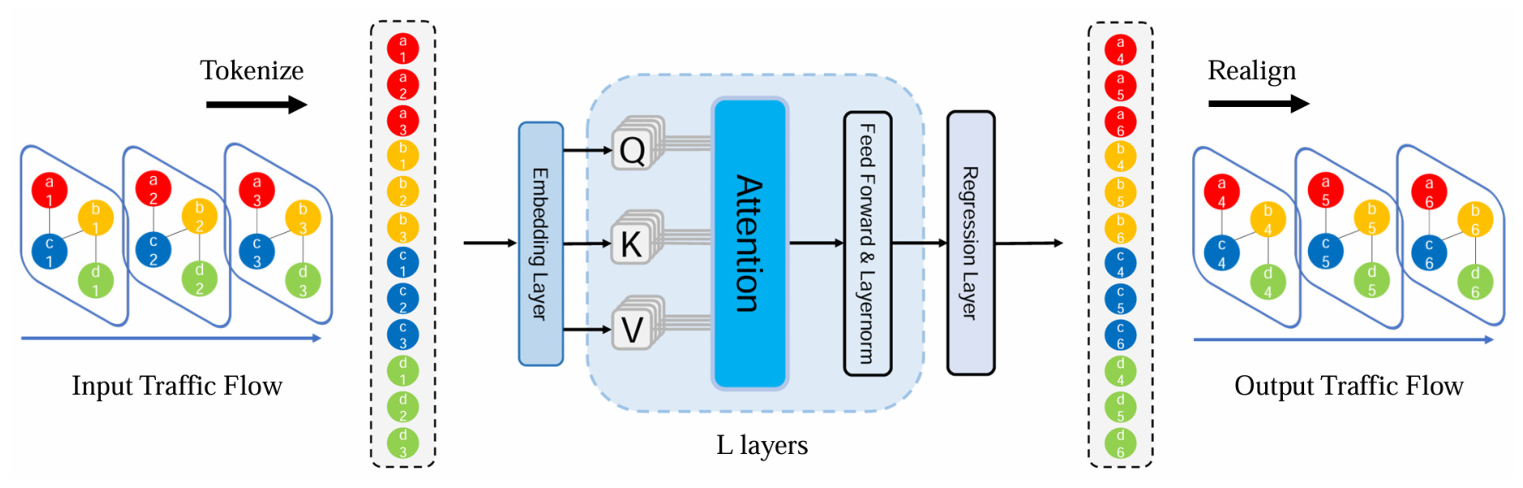
STformer
STformer treats each sensor at different time steps as an independent spatial-temporal token (ST-Token). These tokens are fed into a vanilla Transformer to capture spatial-temporal dependencies dynamically and efficiently. The model achieves state-of-the-art performance but has quadratic complexity.
NSTformer
To overcome the computational complexity of STformer, NSTformer uses the Nyström method to approximate self-attention with linear complexity. This model surprisingly performs slightly better than STformer in some cases, suggesting potential additional benefits of approximate attention.
Experimental Design
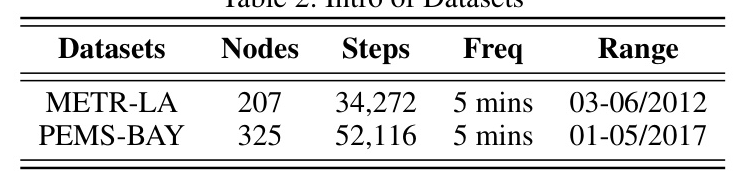
Datasets
The study uses two commonly used traffic forecasting datasets: METR-LA and PEMS-BAY. These datasets provide extensive traffic data, allowing for robust evaluation of the proposed models.
Experimental Setup
The datasets are partitioned into training, validation, and test sets. The models are configured with specific embedding dimensions, Transformer layers, and attention heads. The experiments are conducted on a server with NVIDIA A100 GPU, using Python, Pytorch, and BasicTS platform.
Baselines
The study compares the proposed models with various traditional and deep learning methods, including HA, HI, SVR, VAR, FC-LSTM, DCRNN, AGCRN, GTS, GWNet, MTGNN, STGCN, STSGCN, AST-GCN, GMAN, STID, STNorm, PDFormer, STAEformer, and ST-Mamba.
Results and Analysis
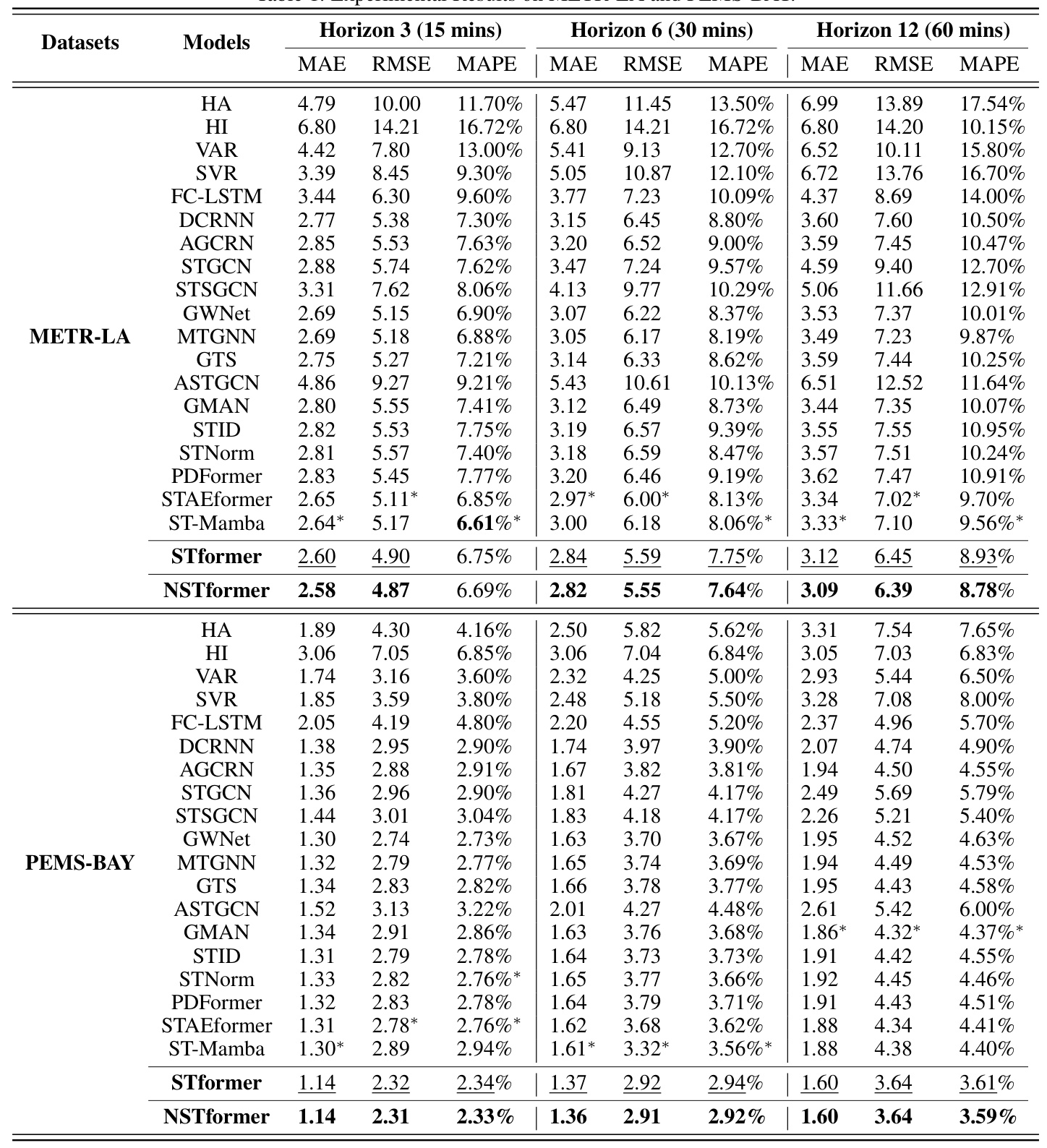
Performance Evaluation
The results show that NSTformer and STformer achieve the best and second-best performance, respectively, on almost all metrics. The slight performance advantage of NSTformer over STformer raises an open question about the potential regularization effect of approximate attention.
Model Complexity
The complexity analysis reveals that NSTformer has linear complexity, making it more computationally efficient than STformer and other models. This efficiency is achieved without compromising performance, highlighting the effectiveness of the proposed approach.

Overall Conclusion
The study demonstrates that pure self-attention is sufficient for spatial-temporal forecasting, achieving state-of-the-art performance with STformer. By adapting the Nyström method, NSTformer further reduces computational complexity while maintaining or even slightly improving performance. This work offers new insights into spatial-temporal forecasting and opens up avenues for future research in applying linear attention mechanisms to other spatial-temporal tasks.
Acknowledgments
The authors express gratitude to Le Zhang, Zezhi Shao, Zheng Dong, and Tsz Chiu Kwok for their valuable insights and assistance in the experiments.