Authors:
Jinluan Yang、Zhengyu Chen、Teng Xiao、Wenqiao Zhang、Yong Lin、Kun Kuang
Paper:
https://arxiv.org/abs/2408.09490
Introduction
Graph Neural Networks (GNNs) have become a cornerstone in learning graph-structured representations, primarily excelling in homophilic graphs where connected nodes share similar features and labels. However, their performance significantly drops when applied to heterophilic graphs, where nodes often connect to others from different classes. This challenge has led to the development of Heterophilic Graph Neural Networks (HGNNs), which aim to extend the neighborhood aggregation mechanism to better handle heterophilic structures.
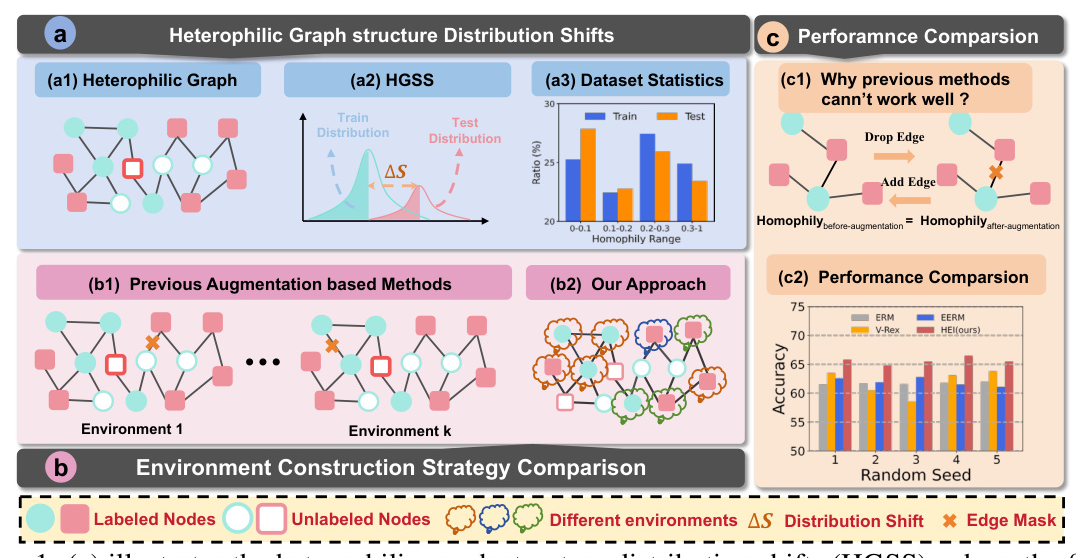
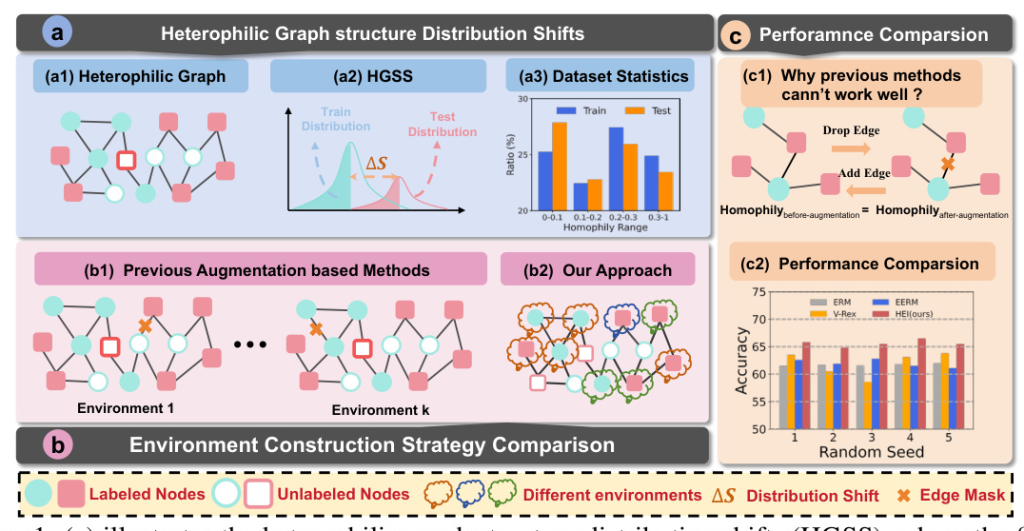
Despite advancements, existing HGNNs often assume a consistent data distribution among nodes, neglecting the distribution shifts between training and testing nodes. This paper introduces the concept of Heterophilic Graph Structure Distribution Shifts (HGSS) and proposes a novel framework, HEI, to generate invariant node representations by incorporating heterophily information without data augmentation.
Related Work
Graph Neural Networks and Heterophily
Traditional GNNs have shown remarkable success in homophilic settings but struggle with heterophilic graphs. Recent works have focused on designing HGNN architectures to address this issue, yet they often overlook the distribution shifts between training and testing nodes.
Invariant Learning
Invariant learning techniques, such as Risk Extrapolation (REx), aim to mitigate distribution shifts by learning representations that remain stable across different environments. However, existing graph-based invariant learning methods often rely on explicit environment construction through data augmentation, which may not effectively address HGSS.
Research Methodology
Problem Formulation
Given a graph ( G = (V, X, A) ) with nodes ( V ), features ( X ), and adjacency matrix ( A ), the goal is to handle node-level out-of-distribution (OOD) problems. The training data ( (G_{train}, Y_{train}) ) comes from a distribution ( p(G, Y|e = e) ), while the test data ( (G_{test}, Y_{test}) ) comes from a different distribution ( p(G, Y|e = e’) ). The objective is to learn a robust model that minimizes loss across different environments.
HEI Framework
The proposed HEI framework aims to generate invariant node representations by inferring latent environments based on estimated neighbor patterns. Unlike previous methods that rely on data augmentation, HEI directly infers environments using similarity metrics to estimate neighbor patterns during the training stage.
Experimental Design
Neighbor Patterns Estimation
The node homophily and edge homophily metrics require true labels, making them unsuitable for the training stage. Instead, similarity metrics such as local similarity, post-aggregation similarity, and SimRank are used to estimate neighbor patterns without label information.
Invariant Learning Framework
HEI utilizes the estimated neighbor patterns to train an environment classifier that assigns nodes to different environments. The framework then trains a set of environment-independent GNN classifiers with a shared encoder, introducing an invariance penalty to improve model generalization.
Complexity Analysis
The overall time complexity of HEI is linear to the scale of the graph, making it efficient for large-scale datasets.
Results and Analysis
Handling Distribution Shifts
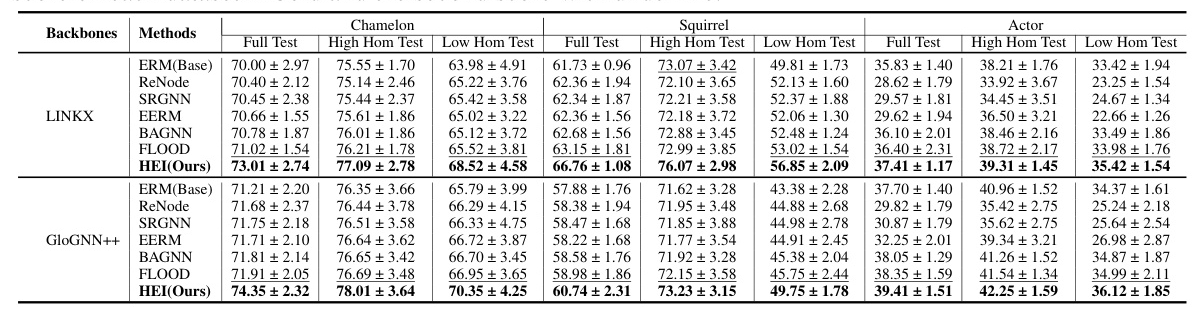
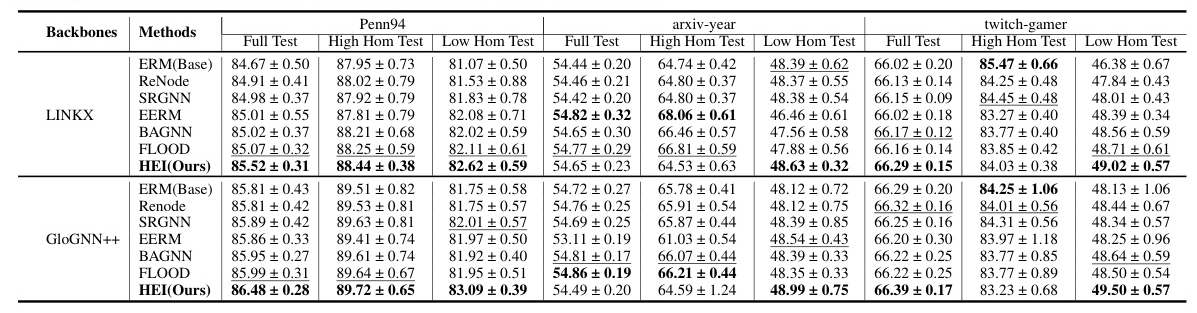
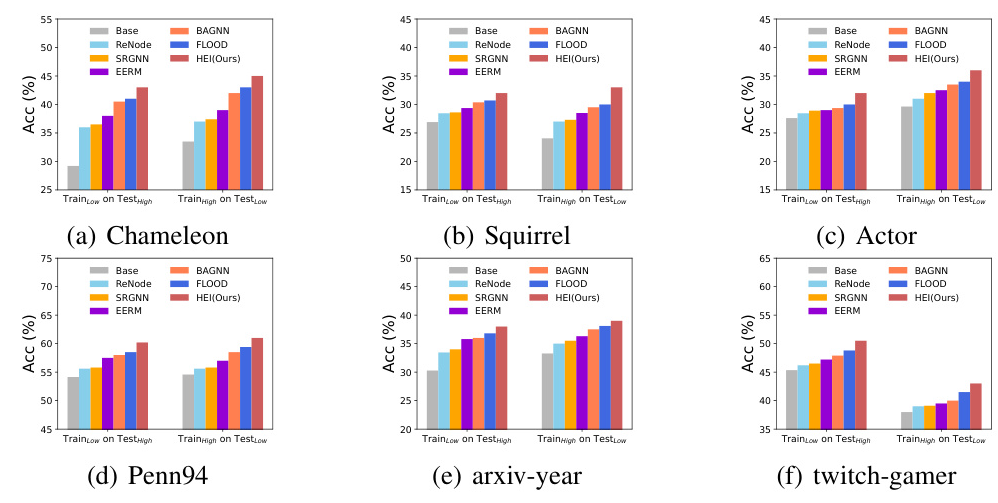
HEI outperforms state-of-the-art methods in addressing HGSS, demonstrating robustness and effectiveness under both standard and severe distribution shift settings. The framework’s ability to infer latent environments without augmentation proves advantageous over existing invariant learning methods.
Impact of Similarity Metrics
Different similarity metrics influence the effectiveness of HEI. SimRank consistently outperforms other metrics, highlighting its ability to capture structural information relevant to distribution shifts.
Sensitivity Analysis
HEI shows stable performance across different numbers of predefined environments, particularly when the number of environments is six or more.
Efficiency Studies
HEI’s additional time cost is acceptable compared to the base GNN backbones, making it a practical solution for large-scale heterophilic graphs.
Overall Conclusion
This paper introduces a novel perspective on heterophilic graph structure distribution shifts and proposes the HEI framework to address this issue. By leveraging estimated neighbor patterns to infer latent environments, HEI significantly improves the generalization and performance of HGNNs. Extensive experiments on various benchmarks and backbones demonstrate the effectiveness of the proposed method, highlighting the importance of considering structural distribution shifts in heterophilic graphs.